Question
The heights, h metres, of the 120 boys in an athletics club are recorded.

The table shows information about the heights of the boys.
(a) (i) Write down the modal class.
……………… \(\leq h < ………………\)
(ii) Calculate an estimate of the mean height.
……………………………………… m
(b) (i) One boy is chosen at random from the club.
Find the probability that this boy has a height greater than 1.8m.
………………………………………….
(ii) Three boys are chosen at random from the club.
Calculate the probability that one of the boys has a height greater than 1.8m and the other
two boys each have a height of 1.4m or less.
………………………………………….
(c) (i) Use the frequency table on page 4 to complete the cumulative frequency table.

(ii) On the grid, draw a cumulative frequency diagram to show this information.

(d) Use your diagram to find an estimate for
(i) the median height,
……………………………………… m
(ii) the 40th percentile.
……………………………………… m
Answer/Explanation
(a)(i)To determine the modal class, we need to identify the class interval with the highest frequency that is 1.5 < h ⩽ 1.6
(ii) 1.62 or 1.623…
(b)(i)\(\frac{14}{120}\)
(ii)\(\frac{21}{20060}\)
(c)(i) 55, 79, 106, 120
(ii) Correct diagram
(d)(i) 1.62 to 1.63
(ii) 1.57 to 1.58
Question
The probability that it rains on Monday \(\frac{3}{5}\)
If it rains on Monday, the probability that it rains on Tuesday is \(\frac{4}{7}\)
If it does not rain on Monday, the probability that it rains on Tuesday is \(\frac{5}{7}\)
(a) Complete the tree diagram.

(b) Find the probability that it rains
(i) on both days,
(ii) on Monday but not on Tuesday,
(iii) on only one of the two days.
(c) If it does not rain on Monday and it does not rain on Tuesday, the probability that it does not
rain on Wednesday is \(\frac{1}{4}\)
Calculate the probability that it rains on at least one of the three days.
Answer/Explanation
(a)

(b)(i) The probability that it rains on both days is:
Product of probabilities when it rained on monday and tuesday:
\(\frac{3}{5}\).\(\frac{4}{7}\)
= \(\frac{12}{35}\)
(ii) The probability that it rains on Monday but not on tuesday:
Product of probabilities when it rained on monday but not on tuesday:
\(\frac{3}{5}\).\(\frac{3}{7}\)
= \(\frac{9}{35}\)
(iii) The probabilities that it rains on only one of the two days:
Addition of the probability of( no rain on Monday and rain on Tuesday), and the( probability of rain on Monday and no rain on Tuesday):
P( No rain on Monday) .P( Rain on Tuesday)+P(Rain on Monday) .P(No rain on Tuesday)
\(\frac{2}{5}\).\(\frac{5}{7}\)+\(\frac{3}{5}\).\(\frac{3}{7}\)
=\(\frac{19}{35}\)
(c) Probability that it rains on at least one of the three days=P(rain on monday).P(no rain on tuesday).P(no rain on wednesday)+P( no rain on monday).P(rain on tuesday).P(no rain on wednesday)+P(no rain on monday).P(no rain on tuesday).P(rain on wednesday)
=\(\frac{34}{35}\)
Question
The table shows information about the heights of 120 girls in a swimming club.
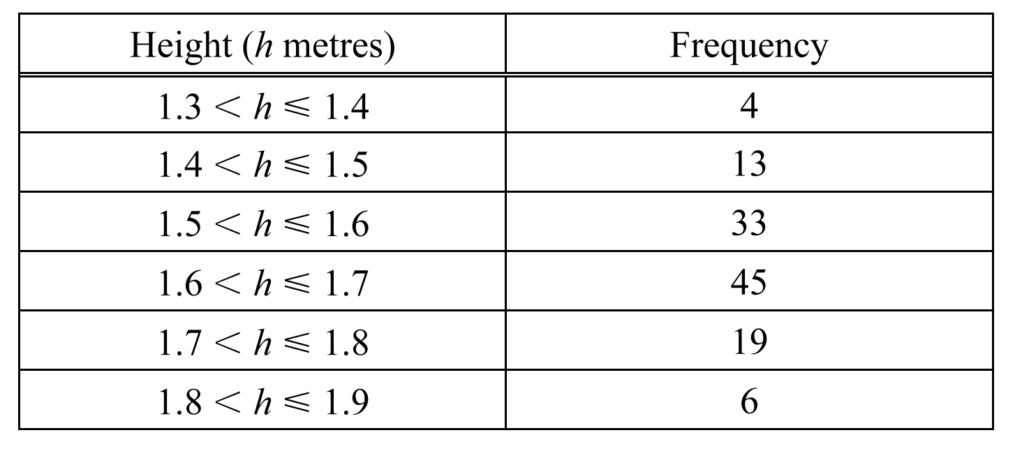
(a) (i) Write down the modal class.
(ii) Calculate an estimate of the mean height. Show all of your working.
(b) Girls from this swimming club are chosen at random to swim in a race.
Calculate the probability that
(i) the height of the first girl chosen is more than 1.8 metres,
(ii) the heights of both the first and second girl chosen are 1.8 metres or less
(c) (i) Complete the cumulative frequency table for the heights.

(ii) Draw the cumulative frequency graph on the grid.

(d) Use your graph to find
(i) the median height,
(ii) the 30th percentile.
Answer/Explanation
(a)(i) Modal class is the class with highest points.
So, here, in the table, highest frequency is 45 with modal class \(1.6< h \leq 1.7\)
(ii) \(\frac{1.3 \times 4 + 1.4 \times 13 + 1.5 \times 33
+ 1.6 \times 45 + 1.7 \times19 + 1.8
\times 6}{120}\)
=1.62
(b)(i) From the table, we can see that,
Modal class \(1.8< h \leq 1.9\) consists of height more than 1.8 m
So, Probability= \(\frac{Given frequency}{Total frequency}\)
=\(\frac{6}{120}\)
(ii) \(\frac{2147}{2380}\)
(c)(i) 