Question
Dan either walks or cycles to school.
The probability that he cycles to school is \(\frac{1}{3}\)
(a) Write down the probability that Dan walks to school.
(b) When Dan cycles to school the probability that he is late is \(\frac{1}{8}\)
When Dan walks to school the probability that he is late is \(\frac{3}{8}\).
Complete the tree diagram.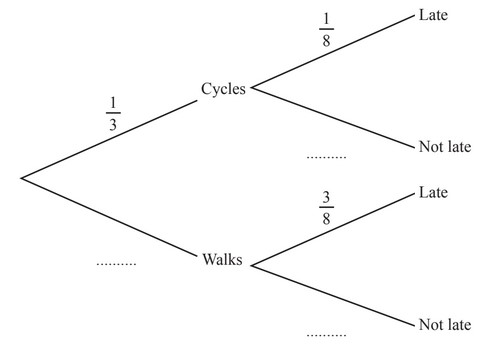
(c) Calculate the probability that
(i) Dan cycles to school and is late,
(ii) Dan is not late.
Answer/Explanation
Ans:
(a) \(\frac{2}{3}\) oe
(b) their \(\frac{2}{3}, \frac{7}{8}, \frac{5}{8}\) oe
(c) (i) \(\frac{1}{24}\) oe
(ii) \(\frac{17}{24}\) oe
Question
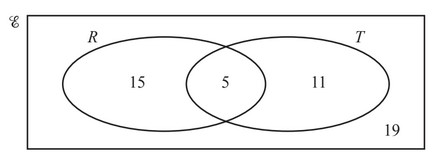
The Venn diagram shows the number of red cars and the number of two-door cars in a car park.
There is a total of 50 cars in the car park.
R = {red cars} and T = {two-door cars}.
(a) A car is chosen at random.
Write down the probability that
(i) it is red and it is a two-door car,
(ii) it is not red and it is a two-door car.
(b) A two-door car is chosen at random.
Write down the probability that it is not red.
(c) Two cars are chosen at random.
Find the probability that they are both red.
(d) On the Venn diagram, shade the region R ∪ T’.(d) On the Venn diagram, shade the region R ∪ T’.
Answer/Explanation
Ans:
(a) (i) \(\frac{5}{50}\) oe
(ii) \(\frac{11}{50}\) oe
(b) \(\frac{11}{50}\) oe
(c) \(\frac{380}{2450}\) oe
(d)
