Question
(a) The probability that Shalini is late for school on any day is\( \frac{1}{6}\)
(i) Complete the tree diagram for Monday and Tuesday.
Monday Tuesday
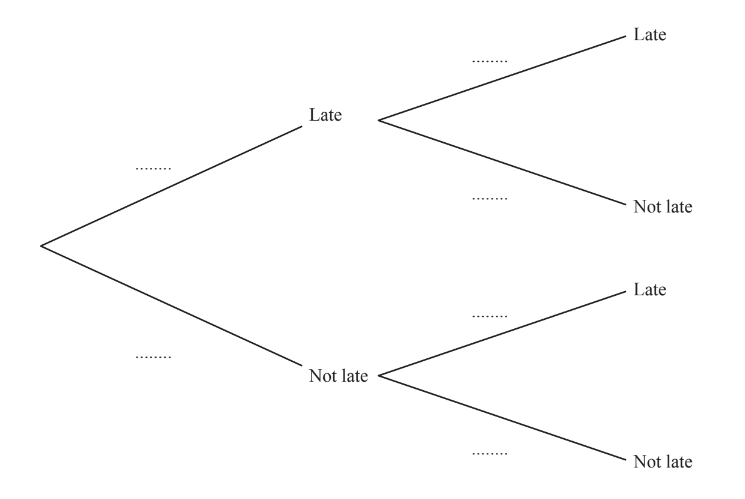
(ii) Calculate the probability that Shalini is late on Monday but is not late on Tuesday.
(b) The Venn diagram shows the number of students in a group of 50 students who wear glasses (G), who wear trainers (T ) and who have a mobile phone (M ).
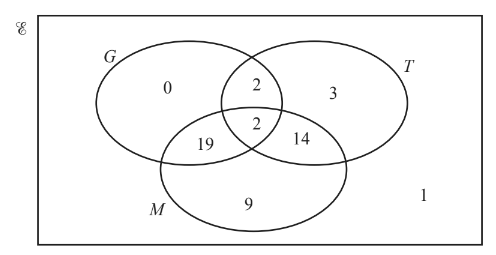
(i) Use set notation to describe the region that contains only one student.
(ii) Find n\( \left ( T’\cap (G\cup M) \right )\)
(iii) One student is picked at random from the 50 students.
Find the probability that this student wears trainers but does not wear glasses.
(iv) Two students are picked at random from those wearing trainers.
Find the probability that both students have mobile phones
Answer/Explanation
.
11(a)(i)\( \frac{1}{6}\) oe on all late branches
11(a)(i) \( \frac{5}{6}\) oe on all late branches
11(a)(ii) \(\frac{5}{36}oe\)
11(b)(i) \( (G\cup T\cup M)’\)oe
11(b)(ii) 28
11(b)(iii) \(\frac{17} {50}oe
11(b)(iv) \(\frac{4}{7}\) oe
Question

The diagram shows 5 cards.
(a) Donald chooses a card at random.
(i) Write down the probability that the number of dots on this card is an even number.[1]
(ii) Write down the probability that the number of dots on this card is a prime number.[1]
(b) Donald chooses two of the five cards at random, without replacement.
He works out the total number of dots on these two cards.
(i) Find the probability that the total number of dots is 5.[3]
(ii) Find the probability that the total number of dots is an odd number.[3]
Answer/Explanation
Ans:
8(a)(i) \(\frac{4}{5}\) oe
8(a)(ii) \(\frac{4}{5}\) oe
8(b)(i) \(\frac{6}{20}\) oe nfww
8(b)(ii) \(\frac{8}{20}\) oe nfww
Question
The probability that it rains on Monday \(\frac{3}{5}\)
If it rains on Monday, the probability that it rains on Tuesday is \(\frac{4}{7}\)
If it does not rain on Monday, the probability that it rains on Tuesday is \(\frac{5}{7}\)
(a) Complete the tree diagram.

(b) Find the probability that it rains
(i) on both days,
(ii) on Monday but not on Tuesday,
(iii) on only one of the two days.
(c) If it does not rain on Monday and it does not rain on Tuesday, the probability that it does not
rain on Wednesday is \(\frac{1}{4}\)
Calculate the probability that it rains on at least one of the three days.
Answer/Explanation
(a)

(b)(i) The probability that it rains on both days is:
Product of probabilities when it rained on monday and tuesday:
\(\frac{3}{5}\).\(\frac{4}{7}\)
= \(\frac{12}{35}\)
(ii) The probability that it rains on Monday but not on tuesday:
Product of probabilities when it rained on monday but not on tuesday:
\(\frac{3}{5}\).\(\frac{3}{7}\)
= \(\frac{9}{35}\)
(iii) The probabilities that it rains on only one of the two days:
Addition of the probability of( no rain on Monday and rain on Tuesday), and the( probability of rain on Monday and no rain on Tuesday):
P( No rain on Monday) .P( Rain on Tuesday)+P(Rain on Monday) .P(No rain on Tuesday)
\(\frac{2}{5}\).\(\frac{5}{7}\)+\(\frac{3}{5}\).\(\frac{3}{7}\)
=\(\frac{19}{35}\)
(c) Probability that it rains on at least one of the three days=P(rain on monday).P(no rain on tuesday).P(no rain on wednesday)+P( no rain on monday).P(rain on tuesday).P(no rain on wednesday)+P(no rain on monday).P(no rain on tuesday).P(rain on wednesday)
=\(\frac{34}{35}\)