Question
a) The box-and-whisker plot shows information about the marks scored by some students in a test.

(i) Write down the median mark. ………………………………………….
(ii) Work out the range.
………………………………………….
(iii) Jais scored a mark in the test that was higher than the marks scored by 75% of the students.
Write down a possible mark for Jais. ………………………………………….
(iv) This box-and-whisker plot shows information about the marks scored by the same students in
a second test.

Make one comparison between the distributions of marks in the two tests.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) The table shows information about the height, h cm, of each of 50 plants.

Calculate an estimate of the mean.
…………………………………….. cm
(c) Some apples are weighed and the mass, m grams, of each apple is recorded.
The table shows the results.
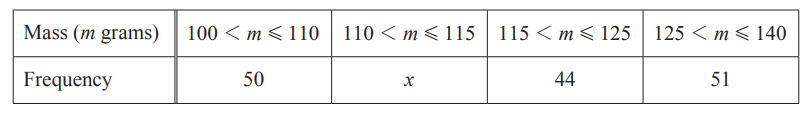
The histogram shows some of the information from the table.

(i) Work out the value of x.
x = …………………………………………
(ii) Complete the histogram.
Answer/Explanation
(a)(i) 70
(ii) 78
(iii) Value in range 86 <V ≤ 90
(iv) One general comment interpreting
the median comparison nfww
e.g. Students did better on second test
oe
OR
One general comment interpreting
IQR/range comparison nfww
e.g. Students marks were more
consistent on the 2nd test oe
(b) 31.2
(c)(i) 38
(ii) Blocks of heights 4.4 and 3.4 with
correct widths
Question
The table shows information about the mass, m grams, of each of 120 letters.

(a) Calculate an estimate of the mean mass. …………………………………….g
(b) Iraj draws a histogram to show this information.
He makes the height of the first bar 17.2cm.
Calculate the height of each of the remaining bars.
(c) Complete the cumulative frequency table.

(d) Draw a cumulative frequency diagram.

(e) Use the cumulative frequency diagram to find an estimate for
(i) the median,
(ii) the upper quartile,
(iii) the 40th percentile,
(iv) the number of letters with a mass m where
Answer/Explanation
5(a) 121 or 120.8… or 120 \(\frac{5}{6}\)
5(b) 12.4 5 1.4
5(c) 43 74 99 120
5(d) Correct diagram
5(e)(i) Strict FT their median reading 1
5(e)(ii) Strict FT their UQ reading 1
5(e)(iii) Strict FT their reading at\( 40^{th}\)percentile
5(e)(iv) Strict FT their reading at 400
– their reading at 250
Question
(a)
The box-and-whisker plots show the times spent exercising in one week by a group of women and
a group of men.
Below are two statements comparing these times.
For each one, write down whether you agree or disagree, giving a reason for your answer.

(b) The frequency table shows the times, t minutes, each of 100 children spent exercising in one week.

(i) Calculate an estimate of the mean time.
…………………………………… min
(ii) The information in the frequency table is shown in this cumulative frequency diagram.

Use the cumulative frequency diagram to find an estimate of
(a) the 60th percentile,
…………………………………… min
(b) the number of children who spent more than 3 hours exercising.
…………………………………………. [2]
(iii) A histogram is drawn to show the information in the frequency table.
The height of the bar for the interval \(60< t\leq 100\) is 10.8 cm.
Calculate the height of the bar for the interval \(160< t\leq 220.\)
…………………………………….. cm
Answer/Explanation
(a) Disagree: the median for the women is
greater (than the median for the men)
oe
Disagree: the men have a smaller
[interquartile] range of times
(b)(i) 87.4
(ii)(a) 90
(ii)(b) 8