Moving Charges and Magnetism Class 12 Important Questions Very Short Answer Type
Question 1.
What is the direction of the force acting on a charged particle q, moving with a velocity \(\overrightarrow{\mathbf{v}}\) in a uniform magnetic field B? (Delhi)
Answer:
The direction of the force acting on a charged particle q, moving with a velocity \(\overrightarrow{\mathbf{v}}\) in a uniform
magnetic field \(\overrightarrow{\mathbf{B}}\) is perpendicular to the plane of vectors \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\)![]()
So, force is perpendicular to both \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\). From equation (i), we can also say that the force \(\overrightarrow{\mathbf{F}}\) acts in the direction of the vectors \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\)
Question 2.
Why should the spring/suspension wire in a moving coil galvanometer have low torsional constant? (All India 2008)
Answer:
Low torsional constant is basically required to increase the current/charge sensitivity in a moving coil ballistic galvanometer.
Question 3.
Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why? (Delhi 2008)
Answer:
At the edges of the solenoid, the field lines get diverged due to other fields and/or non-availability of dipole loops, while in toroids the dipoles (in loops) orient continuously.
Question 4.
An electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field? (All India 2009)
Answer:![]()
∴Magnetic field will be in the line of the velocity of electron.
Question 5.
A beam of a particles projected along +x-axis, experiences a force due to a magnetic field along the +y-axis. What is the direction of the magnetic field? (All India 2009)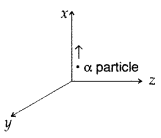
Answer:![]()
Direction of the magnetic field is towards negative direction of z-axis.
Question 6.
A beam of electrons projected along +x-axis, experiences a force due to a magnetic field along the +y/-axis. What is the direction of the magnetic field? (All India 2010)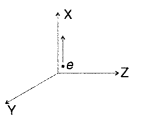
Answer:
Direction of the magnetic field is F = q (v × B) towards positive direction of z-axis.
Question 7.
A beam of protons, projected along + x-axis, experiences a force due to a magnetic field along the – y-axis. What is the direction of the magnetic field? (All India 2010)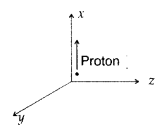
Answer:
The direction of the magnetic field is towards positive direction of z-axis.
Question 8.
Depict the trajectory of a charged particle moving with velocity v as it enters a uniform magnetic field perpendicular to the direction of its motion. (Comptt. All India 2012)
Answer: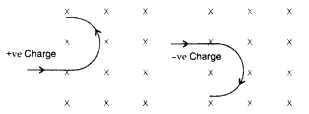
The force acting on the charge particle will be perpendicular to both v and S and therefore will describe a circular path.
Question 9.
Write the expression in vector form, for the magnetic force \(\overrightarrow{\mathrm{F}}\) acting on a charged particle moving with velocity \(\overrightarrow{\mathrm{V}}\) in the presence of a magnetic field B. (Comptt. All India 2012)
Answer: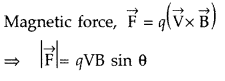
Question 10.
An ammeter of resistance 0.6 Ω can measure current upto 1.0 A. Calculate
(i) The shunt resistance required to enable the ammeter to measure current upto 5.0 A
(ii) The combined resistance of the ammeter and the shunt. (Delhi 2013)
Answer: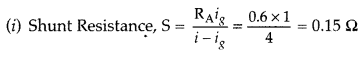
Question 11.
Write the expression, in a vector form, for the Lorentz magnetic force \(\overrightarrow{\mathrm{F}}\) due to a charge moving with velocity \(\overrightarrow{\mathrm{V}}\) in a magnetic field \(\overrightarrow{\mathrm{B}}\). What is the direction of the magnetic force? (Delhi 2013)
Answer:![]()
… [q is the magnitude of the moving charges)
This force is normal to both the directions of velocity \(\overrightarrow{\mathrm{V}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\) .
Question 12.
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current. (All India 2013)
Answer:![]()
“One ampere of current is the value of steady current, which when maintained in each of the two very long, straight, parallel conductors of negligible cross-section; and placed one metre apart in vacuum, would produce on each of these conductors a force of equal to 2 × 10-7 newtons per metre (Nm-1) of length. ”
Question 13.
Write the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields.(Comptt. All India 2013)
Answer:![]()
and electric and magnetic fields are mutually perpendicular.
Question 14.
Why do the electrostatic field lines not form closed loops? (All India 2015)
Answer:
Electric field lines do not form closed loops because the direction of an electric field is from positive to negative charge. So one can regard a line of force starting from a positive charge and ending on a negative charge. This indicates that electric field lines do not form closed loops.
Question 15.
A particle of mass ‘m’ and charge ‘q’ moving with velocity V enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected? (Comptt. Delhi 2015)
Answer:
Kinetic energy will NOT be affected.
*(When \(\vec{v}\) is perpendicular to \(\vec{B}\), then magnetic field provides necessary centripetal force)
Question 16.
Write the underlying principle of a moving coil galvanometer. (Delhi 2015)
Answer:
Principle of a galvanometer : “A current carrying coil, in the presence of magnetic field, experiences a torque which produces proportionate deflection”.![]()
Question 17.
A coil, of area A, carrying a steady current I, has a magnetic moment, \(\vec{m}\), associated with it. Write the relation between \(\vec{m}\), I and A in vector form. (Comptt Delhi 2015)
Answer:
Relation for magnetic moment = \(\vec{m}\) = I\(\vec{A}\)
Question 18.
Using Ampere’s circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns. (All India 2008)
Answer:
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I0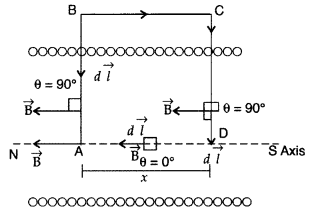
Applying Ampere’s circuital loop — | B .dl = go I ’
![]()
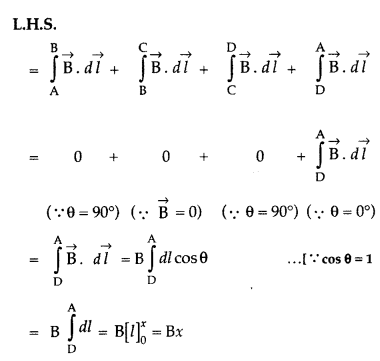
No. of turns in x length = nx,
Current in turns nx, I = nx I0
According to Ampere’s circuital law
Bx = µ0 I => Bx = µ0 nx I0
∴ B = µ0nI0
Question 19.
A charge ‘q’ moving B along the X-axis with a velocity v is subjected to a uniform magnetic field B acting along the Z-axis as it crosses the origin O. (Delhi 2009)
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.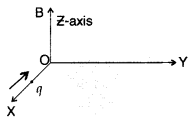
Answer: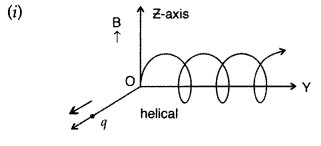
(ii) K.E does not change irrespective of the direction of the charge as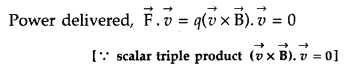
Question 20.
State Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element \(\overrightarrow{d \vec{l}}\) at point P situated at a distance \(\vec{r}\) from the element as shown in the figure.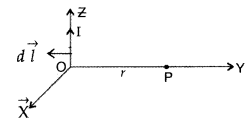
Answer:
Biot-Savart law and its applications :
Biot-Savart law states that “the magnitude of the magnetic field dB at any point due to a small current element dl is given by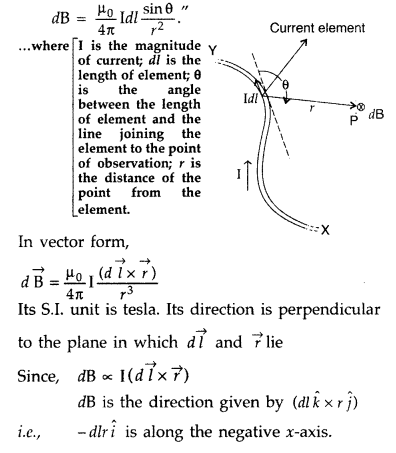
Question 21.
(a) In what respect is a toroid different from a solenoid? Draw and compare the pattern of the magnetic field lines in the two cases.
(b) How is the magnetic field inside a given’ solenoid made strong? (All India 2011)
Answer:
(a) Solenoid consists of a long wire wound in the form of a helix where the neighbouring turns are closely spaced, whereas, the toroid is a hollow circular ring on which a large number of turns of a wire is closely wound.
(b) Magnetic field inside a given solenoid is made strong by putting a soft iron core inside it. It is strengthened by increasing the amount of current through it.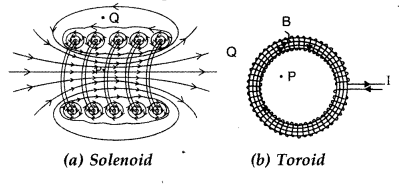
Question 22.
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\). Show that no work is done by this force on the charged particle. (All India 2011)
Answer:
Expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\) is \(\vec{F}\) = q(\(\vec{E}\) + \(\vec{v}\) × \(\vec{B}\))
Work done by a magnetic force on a charged particle :
The magnetic force \(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{E}}+\vec{v} \times \overrightarrow{\mathrm{B}})\) always acts perpendicular to the velocity \(\vec{v}\) on the direction of motion of charge q.![]()
Question 23.
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force. (All India 2011)
Answer:
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A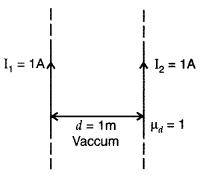
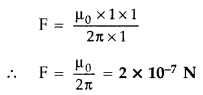
Question 24.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis. (All India 2011)
Answer:
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I0 Applying Ampere’s circuital loop — | B .dl = go I ’
Applying Ampere’s circuital loop — | B .dl = go I ’![]()
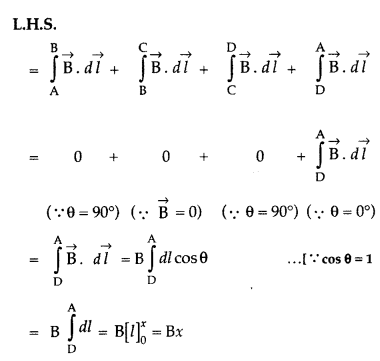
No. of turns in x length = nx,
Current in turns nx, I = nx I0
According to Ampere’s circuital law
Bx = µ0 I => Bx = µ0 nx I0
∴ B = µ0nI0
Question 25.
Two identical circular wires P and Q each of radius R and carrying current ‘I’ are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils. (Delhi 2011)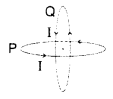
Answer:
Magnetic field produced by the two coils at their common centre are: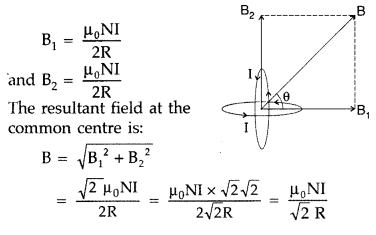
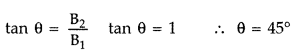
The net magnetic field is directed at an angle of 45° with either of the fields.
Question 26.
Two identical circular loops, P and Q, each of radius r and carrying current I and 21 respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O. (Delhi 2011)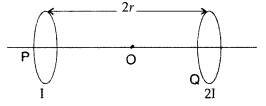
Answer:
When the currents are in the same direction, the resultant field at point O is,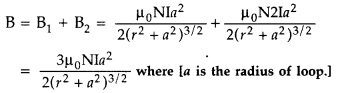
Question 27.
Two identical circular loops, P and Q, each of radius r and carrying equal currents are kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O. (Delhi 2011)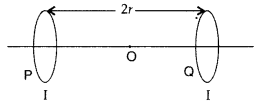
Answer: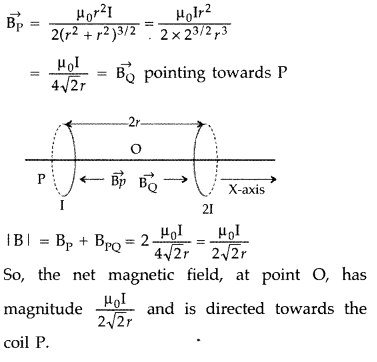
Question 28.
A circular coil of closely wound N turns and radius r carries a current I. Write the expressions for the following :
(i) the magnetic field at its centre
(ii) the magnetic moment of this coil (All India 2011)
Answer:
(i) The magnetic field at the centre of a circular coil of N turns and radius r carrying a current, I is![]()
(iii) Magnetic moment, M = NIA = NIπr2
Question 29.
A proton and a deuteron, each moving with velocity \(\vec{v}\) enter simultaneously in the region of magnetic field \(\vec{B}\) acting normal to the direction of velocity. Trace their trajectories establishing the relationship between the two. (Comptt. Delhi 2011)
Answer: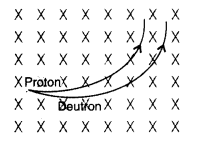
Question 30.
A particle of mass 10-3 kg and charge 5 pC enters into a uniform electric field of 2 × 105 NC-1, moving with a velocity of 20 ms-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest. (Comptt. Delhi 2011)
Answer: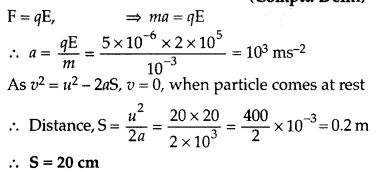
Question 31.
A particle of mass 2 x 10-3 kg and charge 2 µC enters into a uniform electric field of 5 × 105 NC-1, moving with a velocity of 10 ms-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest. (Comptt. Delhi 2011)
Answer:
Force applied on the charged particle, f = qE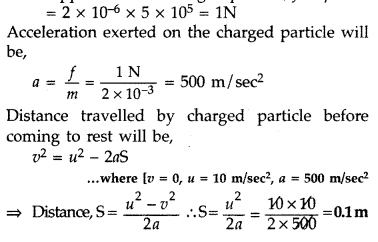
Question 32.
A particle of mass 5 × 10-3 kg and charge 4 µC enters into a uniform electric field of 2 × 105 NC-1, moving with a velocity of 30 ms-1 in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest. (Comptt. Delhi 2011)
Answer:
Force applied on the charged particle,![]()
Acceleration exerted on the charged particle when it enters in electric field.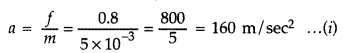
Distance travelled by charged particle before coming to rest will be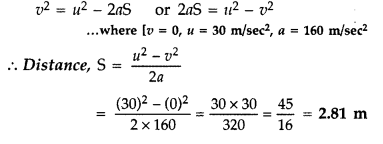
Question 33.
An ammeter of resistance 0.80 Ω can measure current upto 1.0 A.
(i) What must be the value of shunt resistance to enable the ammeter to measure current upto 5.0A?
(ii) What is the combined resistance of the ammeter and the shunt? (Delhi 2013)
Answer:
Question 34.
(a) How is a toroid different from a solenoid?
(b) Use Ampere’s circuital law to obtain the magnetic field inside a toroid.
(c) Show that in an ideal toroid, the magnetic field
(i) inside the toroid and
(ii) outside the toroid at any point in the open space is zero. (Comptt. All India 2014)
Answer:
(a) A toroid is essentially a solenoid which has been bent into a circular shape to close on itself.
(b)
(b) A toroid is a solenoid bent to form a ring shape.
Let N number of turns per unit length of toroid and I be current flowing in it.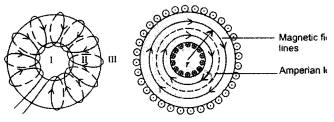
Consider a loop (region II) of radius r passes through the centre of the toroid.
Let (region II) \(\overrightarrow{\mathrm{B}}\) be magnetic field along the loop is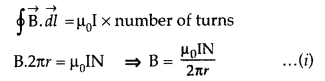
Let (region I) B1 be magnetic field outside toroid in open space. Draw an amperian loop L2 of radius r2 through point Q.
Now applying ampere’s law :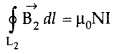
As I = 0, because the circular turn current coming out of plane of paper is cancelled exactly by current going into it, so net I = 0, equation (i) becomes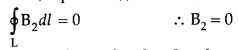
(c) For the loop 1, Ampere’s circuital law gives,![]()
Thus the magnetic field, in the open space inside the toroid is zero.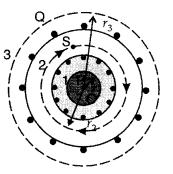
Also at point Q, we have![]()
But from the sectional cut, we refer to that the current coming out of the plane of the paper is cancelled exactly by the current going into it
Hence Ienclosed = 0
∴ B3 = 0
Question 35.
Derive an expression for the magnetic moment (\(\vec{\mu}\)) of an electron revolving around the nucleus in terms of its angular momentum ![]() . What is the direction of* the magnetic moment of the electron with respect to its angular momentum? (Comptt. All India 2014)
. What is the direction of* the magnetic moment of the electron with respect to its angular momentum? (Comptt. All India 2014)
Answer: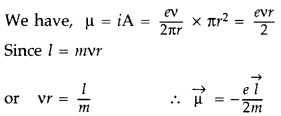
[ ∴ electron has a negative charge
The direction of (\(\vec{\mu}\)) is opposite to that of ![]() , because of the negative charge of the electron.
, because of the negative charge of the electron.
Question 36.
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies.
(Delhi 2014)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.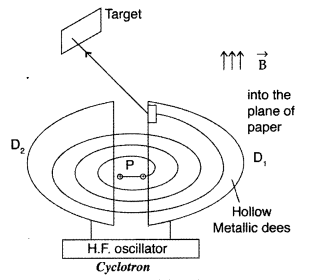
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than
before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
Question 37.
Draw the magnetic field lines due to a current passing through a long solenoid. Use Ampere’s circuital law, to obtain the expression for the magnetic field due to the current I in a long solenoid having n number of turns per unit length. (Comptt. Delhi 2014)
Answer: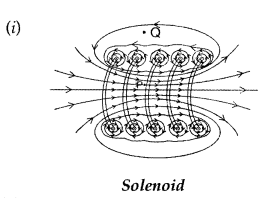
(ii) Expression for magnetic field :
Magnetic field due to Solenoid Let length of solenoid = L
Total number of turns in solenoid = N
No. of turns per unit length = \(\frac{N}{L}\) = n
ABCD is an Ampere’s loop
AB, DC are very large
BC is in a region of \(\overrightarrow{\mathrm{B}}\) = 0
AD is a long axis
Length of AD = x
Current in one turn = I0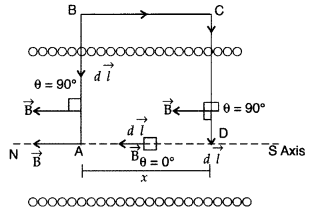
Applying Ampere’s circuital loop — | B .dl = go I ’![]()
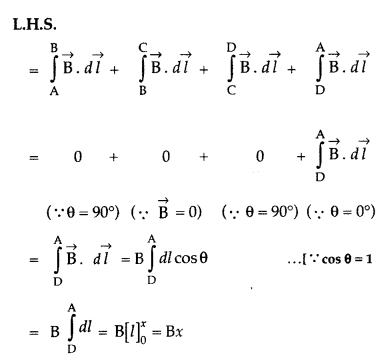
No. of turns in x length = nx,
Current in turns nx, I = nx I0
According to Ampere’s circuital law
Bx = µ0 I => Bx = µ0 nx I0
∴ B = µ0nI0
Question 38.
A rectangular coil of sides ‘V and ‘b’ carrying a current I is subjected to a uniform magnetic field \(\overrightarrow{\mathbf{B}}\) acting perpendicular to its plane. Obtain the expression for the torque acting on it.
(Comptt. Delhi 2014)
Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)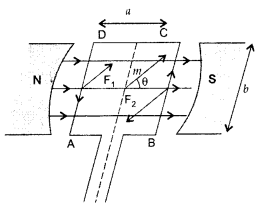
Force exerted on the arm DA inward
F1 = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F2 = I b B ∴ F2 = F1
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,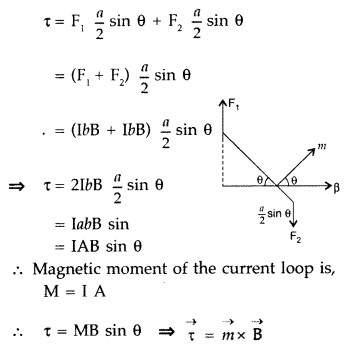
If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.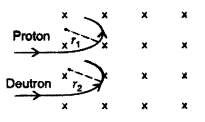
Question 39.
(i) State Biot – Savart law in vector form expressing the magnetic field due to an \(\overrightarrow{\mathbf{B}}\) element \(\overrightarrow{\mathbf{dl}}\) carrying current I at a distance \(\overrightarrow{\mathbf{r}}\) from the element.
(ii) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius r carrying a steady current I. Draw the field lines due to the current loop. (Comptt. All India 2014)
Answer:
(i) According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.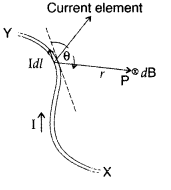
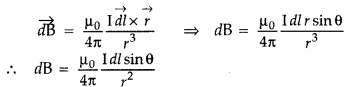
Magnetic field on the axis of circular current loop :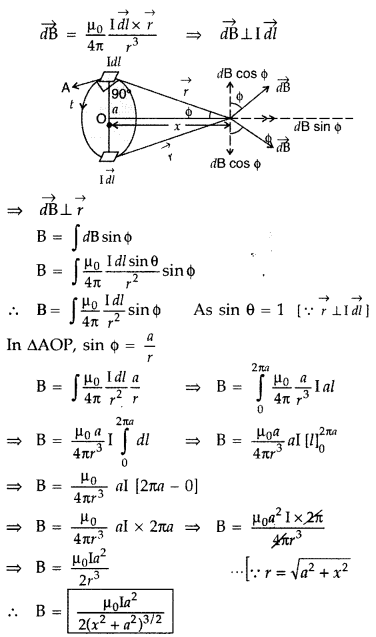
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
Question 40.
A square loop of side 20 cm carrying current of 1A is kept near an infinite long straight wire carrying a current of 2A in the same plane as shown in the figure.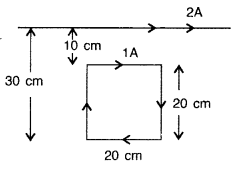
Calculate the magnitude and direction of the net force exerted on the loop due to the current carrying conductor. (Comptt. All India)
Answer: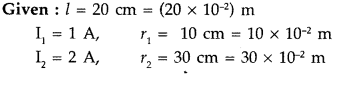
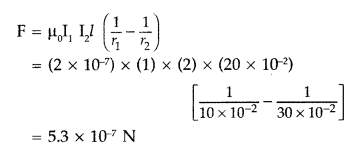
The direction of force is towards the infinitely long straight wire.
Question 41.
A square shaped plane coil of area 100 cm2 of 200 turns carries a steady current of 5A. It is placed in a uniform magnetic field of 0.2 T acting perpendicular to the plane of the coil. Calculate the torque on the coil when its plane makes an angle of 60° with the direction of the field. In which orientation will the coil be in stable equilibrium? (Comptt. All India 2014)
Answer: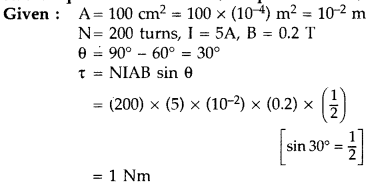
The coil will be in stable equilibrium when it is parallel to the magnetic field.
Question 42.
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed. (All India 2015)
Answer:
Condition: The velocity \(\vec{v}\) of the charged particles, and the \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) vectors, should be mutually perpendicular
It means that the forces on q, due to \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) must be oppositely directed.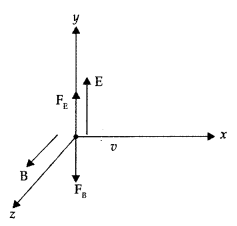

Question 43.
A charge q of mass m is moving with a velocity of v, at right angles to a uniform magnetic field B. Deduce the expression for the radius of the circular path it describes. (Comptt. Delhi 2015)
Answer:
Force experienced by charged particle in magnetic field.![]()
As v and B are perpendicular, F = qvB
This force is perpendicular to the direction of velocity and hence acts as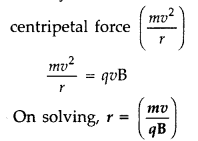
Question 44.
A proton and an alpha particle having the same kinetic energy are, in turn, passed through a region of uniform magnetic field, acting normal to the plane of the paper and travel in circular paths. Deduce the ratio of the radii of the circular paths described by them. (Comptt. Delhi 2015)
Answer: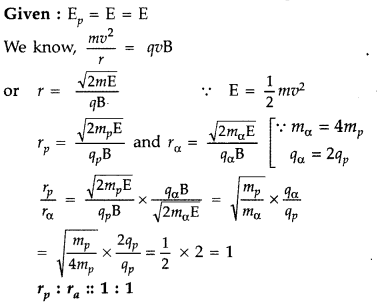
Moving Charges and Magnetism Class 12 Important Questions Short Answer Type SA III
Question 45.
A circular coil of 200 turns and radius 10 cm is placed in a uniform magnetic field of 0.5 T, normal to the plane of the coil. If the current in the coil is 3.0 A, calculate the
(a) total torque on the coil.
(b) total force on the coil.
(c) average force on each electron in the coil, due to the magnetic field.
Assume the area of cross-section of the wire to be 10-5 m2 and the free electron density is 1029/m3. (All India 2015)
Answer: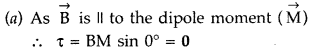
(b) As the forces on different parts of the coil appears in pairs, equal in magnitude and opposite in direction, net force on the coil is zero.i.e., F = 0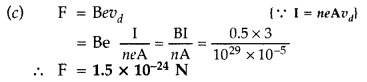
Question 46.
An electron moves around the nucleus in a hydrogen atom of radius 0.51 A, with a velocity of 2 × 105 m/s. Calculate the following :
(i) the equivalent current due to orbital motion of electron
(ii) the magnetic field produced at the centre of the nucleus
(iii) the magnetic moment associated with the electron. (All India 2015)
Answer: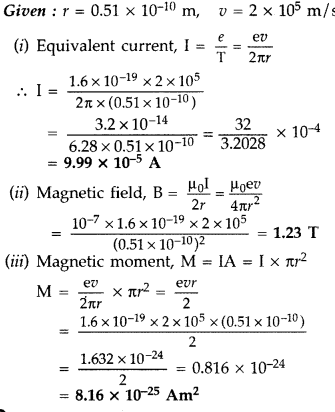
Question 47.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere. (Delhi 2015)
Answer:
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A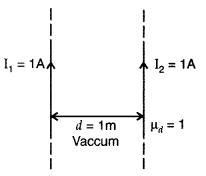
Question 48.
Explain the principle and working of a cyclotron with the help of a schematic diagram. Write the expression for cyclotron frequency. (Delhi 2015)
Answer:
Cyclotron :
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.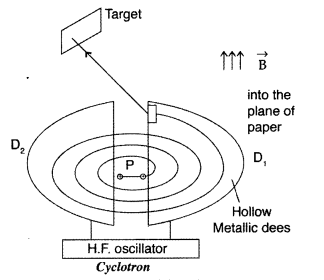
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
Question 49.
Find the magnetic field at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of the circular coil carrying current.
Answer:
Magnetic field at a point on the axis of a circular coil carrying current
Consider a circular coil of radius ‘a’ with centre ‘O’, carrying current I. Its plane is perpendicular to the plane of the loop. Suppose P is any point on the axis of the circular coil at a distance x from the centre, such that
OP = x
Consider two small elements of length dl at C and D at diametrically opposite current elements of the coil
PC = PD = r = \(\sqrt{a^{2}+x^{2}}\)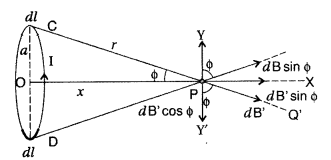
According to Biot Savart’s law, the magnitude of magnetic field at P due to current element dl at C is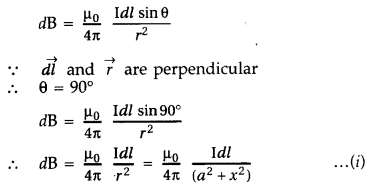
The direction of \(\overrightarrow{d \overrightarrow{\mathrm{B}}}\) is perpendicular to \(\vec{r}\) in the plane paper i.e., along PQ.
Similarly, the magnitude of magnetic field at P due to current element dl at D is![]()
Its direction is along PQ’
From (i) an (ii), we get, dB = dB’ = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d l}{\left(a^{2}+x^{2}\right)}\)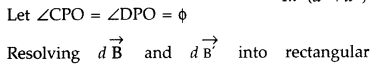
components :
(i) dB cos ϕ along PY and dB’ sin ϕ along PX
(ii) dB cos ϕ along PY and dB’ sin ϕ along PX
Since the components of the magnetic field along Y-axis are equal and opposite and cancel each other, the components along X-axis are in the same direction and are added up.
Hence the total magnetic field at point P is,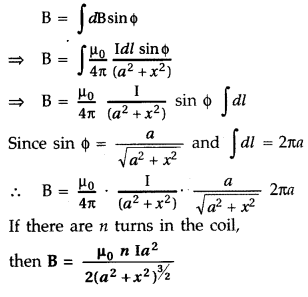

Question 50.
Deduce the expression for the magnetic dipole moment of an electron orbiting around the central nucleus. (All India 2010)
Answer:
Consider an electron revolving around the nucleus of an atom. Electron is in uniform circular motion around the nucleus of charge + Ze. This constitutes a current.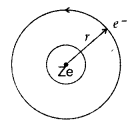
![]()
If ‘r’ is orbital radius of the electron and ‘V’ is orbital speed, then the time period is![]()
Now putting the value of T in (i), we get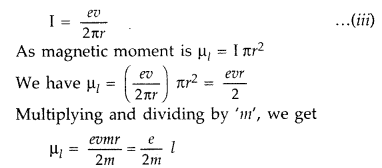
…where [Z is angular momentum of the electron.
According to Bohr hypothesis angular momentum we can have discrete values only.![]()
Question 51.
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point V in the region for
(i) r < a and (ii) r > a.
Answer:
Consider an infinite long thick wire of radius V with axis XY. Let I be the current flowing through the wire.
When the point P lies outside the wire :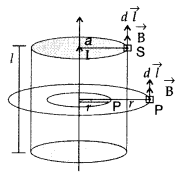
Let r be the perpendicular distance of point P from the axis of the cylinder, where r > a.
Here \(\overrightarrow{\mathrm{B}}\) and d \(\overrightarrow{\mathrm{l}}\) are acting in the same direction.
Applying Ampere’s circuital law, we have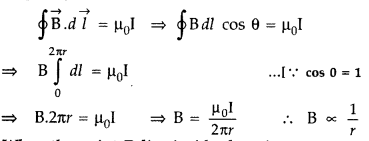
When the point P lies inside the wire :
Here r ≤ a. We have two possibilities:
According to Ampere circuital law,
(i) “Whenever the current floras only through the surface of the wire, B = 0 as current in the closed path will be zero.”
(ii) “Wherever in the case when current is uniformly distributed through the cross-section of conductor, current through the closed path will be :
I’ = Current per unit area of the wire × area of the circle of radius r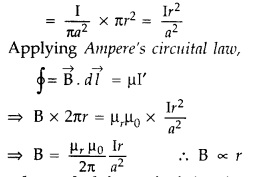
Question 52.
State the underlying principle of working of a moving coil galvanometer. Write two reasons why a galvanometer can not be used as such to measure current in a given circuit. Name any two factors on which the current sensitivity of a galvanometer depends. (Delhi 2010)
Answer:
(i) Moving coil galvanometer works on the principle of a torque experienced by a current carrying coil placed in a magnetic field, whose magnitude is a function of current passing through the coil.
(ii) The galvanometer cannot be used to measure the value of the current in a given circuit due to the following two reasons:
(a) Galvanometer is a very sensitive device. It gives a full scale deflection for a small value of current.
(b) The galvanometer has to be connected in series for measuring currents and as it has a large resistance, this will change the value of the current in the circuit.
(iii)![]()
It depends on the number of turns N of the coil, torsion constant and the area A of the coil.
Question 53.
Write the expression for the magnetic moment (\(\overrightarrow{\mathbf{M}}\)) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form. In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I, at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop. (Delhi 2010)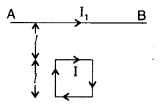
Answer:
(i) The magnetic moment \((\overrightarrow{\mathrm{M}})\) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form is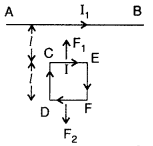
![]()
(ii) CE will be attracted towards AB with a force F1 given by
Question 54.
Write the expression for the magnetic moment (\(\overrightarrow{\mathbf{M}}\)) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form. In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I, at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop. (Delhi 2010)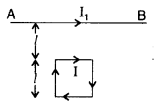
Answer:
(i) The magnetic moment \((\overrightarrow{\mathrm{M}})\) due to a planar square loop of side ‘l’ carrying a steady current I in a vector form is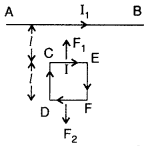
![]()
(ii) CE will be attracted towards AB with a force F1 given by
Question 55.
A rectangular loop of wire of size 4 cm × 10 cm carries a steady current of 2 A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and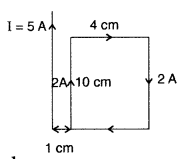
(ii) the magnitude and direction of the force on the loop due to the current carrying wire. (Delhi 2012)
Answer:
τ = IAB sin θ => τ = IAB sin θ (as θ = 0)![]()
(ii) Force acting on the loop on |F|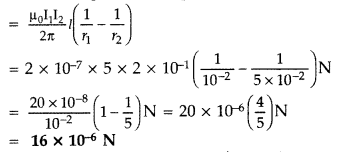
Direction : Towards conductor/Attractive Net force on the loop will act towards the long conductor (attractive) if the current in its closer side is in the same direction as the current in the long conductor, otherwise it will be repulsive.
Question 56.
A rectangular loop of wire of size 2 cm × 5 cm carries a steady current of 1 A. A straight long wire carrying 4 A current is kept near the loop as shown in the figure.
If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire. (Delhi 2010)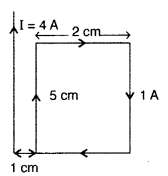
Answer:
(i) τ (Torque on the loop) = MB sin θ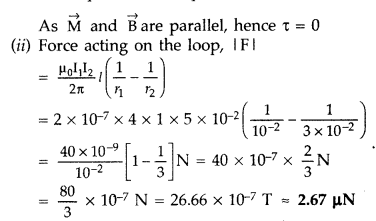
Direction : Towards the conductor/Attractive
Net force on the loop will act towards the long conductor (attractive) if the current in its closer side is in the same direction as the
current in the long conductor, otherwise it will be repulsive.
Question 57.
Two identical coils, each of radius ‘R’ and number of turns ‘N’ are lying in perpendicular planes such that their centres coincide. Find the magnitude and direction of the resultant magnetic field at the centre of the coils, if they are carrying currents ‘I’ and √3I respectively.
(Comptt. Delhi 2010)
Answer: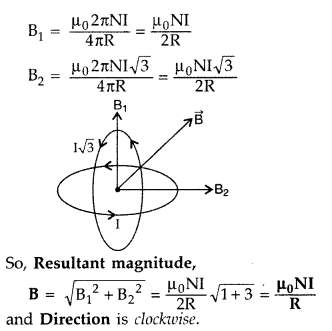
Question 58.
Two identical coils, each of radius ‘R’ and number of turns ‘N’ are lying in perpendicular planes such that their centres coincide. Find the magnitude and direction of the resultant magnetic field at the centre of the coils, if they are carrying currents ‘I’ and √2I respectively.
(Comptt. Delhi 2010)
Answer: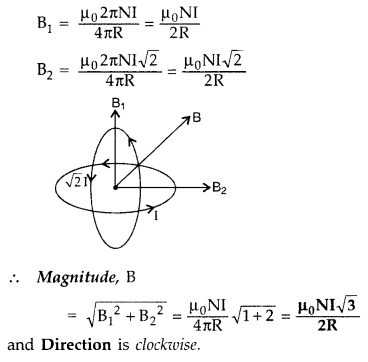
Question 59.
Figure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a velocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for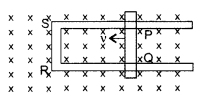
(i) the current in the loop
(ii) the force and
(iii) the power required to move the arm PQ. (Delhi 2010)
Answer:
Let the magnetic field acting on the loop be B and length of the rod PQ be l
The induced e.m.f. ε = Blv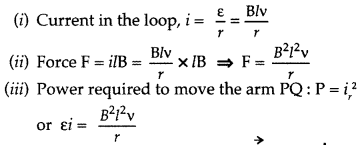
Question 60.
A rectangular conductor LMNO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10 ms-1, calculate the emf induced in the arm. Given the resistance of the arm to be 5Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm. (All India 2010)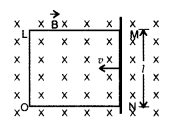
Answer: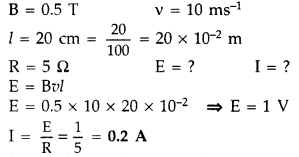
Question 61.
A wire AB is carrying a steady current of 12A and is lying on the table. Another wire CD carrying 5A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms-2] (All India 2010)
Answer:
Given :
Current in the wire AB (I1) = 12 A,
Current in wire CD (I2) = 5 A
Separation between two wires (d) = 1 mm
= 10-3 m
Let ‘m’ be the mass of wire CD of length (L),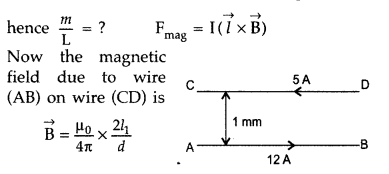
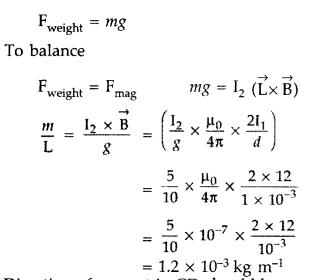
Direction of current in CD should be opposite to that of AB.
Question 62.
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD carrying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms-2] (All India 2010)
Answer:
Let AB has current in +ve x-direction
(I1) Current in wire AB = 10 A,
(I2) Current in wire CD = 6 A
Separation between the two wires = 2 mm
= 2 × 10-3m
To keep the wire CD suspended in its vertical position when left free. For this magnetic force on CD due to AB should balance mg due to its own weight.
Let m be the mass of the wire CD and L be its length
Direction of current in CD should be opposite to that AB.
Question 63.
(a) Define the current sensitivity of a galvanometer.
(b) The coil area of a galvanometer is 16 × 10-4 m2. It consists of 200 turns of a wire and is in a magnetic field of 0.2 T. The restoring torque constant of the suspension fibre is 10-6 Nm per degree. Assuming the magnetic field to be radial, calculate the maximum current that can be measured by the galva-nometer if the scale can accommodate 30° deflection. (Comptt. All India 2010)
Answer:
Sensitivity of a galvanometer: A galvanometer is said to be sensitive, if it gives a large deflection, even when a small current passes through it.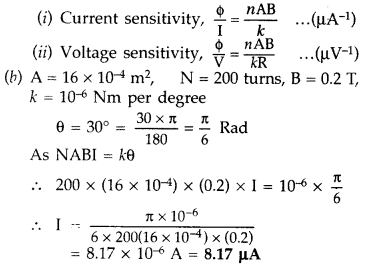
Question 64.
(a) State Ampere’s circuital law, expressing it in the integral form.
(b) Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current “I” flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current “l” flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) inside on the axis and
(ii) outside the combined system. (Delhi 2014)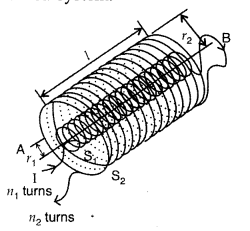
Answer:
(a) According to Ampere’s Circuital law, the magnetic field B is related to steady current![]()
(i) Inside the combined system : Magnetic field at a point on the axis.
Using Ampere’s Circuital law, the magnetic field due to inner solenoid S1 is given by![]()
Similarly due to outer solenoid S2,![]()
Since these two magnetic fields are opposite in direction,![]()
in the upward direction.
(ii) Outside the combined system : At such a point, magnetic field is zero, because corresponding turns of the two halves of the solenoid produce equal and opposite magnetic fields.
Question 65.
Consider the motion of a charged particle of mass ‘m’ and charge ‘q’ moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\).
(a) If \(\vec{v}\) is perpendicular to \(\vec{B}\), show that it describes a circular path having angular frequency ω = qB/m.
(b) If the velocity \(\vec{v}\) has a component parallel to the magnetic field \(\vec{B}\), trace the path described by the particle. Justify your answer. (Comptt. Delhi 2014)
Answer:
(a) When a charged particle with charge q moves inside a magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity v, it experiences a force, which is given by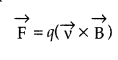
Here, \(\overrightarrow{\mathrm{v}}\) is perpendicular to \(\overrightarrow{\mathrm{B}}\), \(\overrightarrow{\mathrm{F}}\) is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.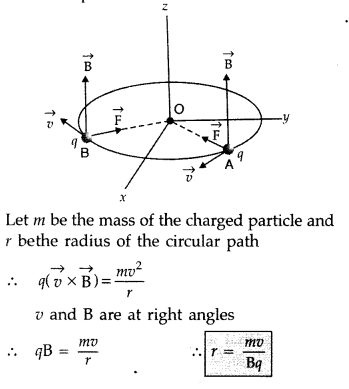
Let m be the mass of the charged particle and r be the radius of the circular path.
Time period of circular motion of the charged particle can be calculated as shown below:
Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of tire particle.
(b)
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.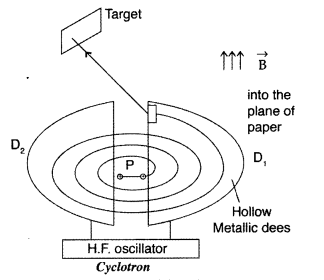
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than
before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
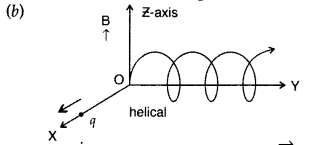
Justification : Component of velocity \(\vec{v}\), parallel to magnetic field, will make the particle move along the field.
Perpendicular component of velocity \(\vec{v}\) will cause the particle to move along a circular path in the plane perpendicular to the magnetic field Hence, the particle will follow a helical path, as shown above.
Question 66.
(a) Draw a schematic sketch of a moving coil galvanometer and describe briefly its working.
(b) “Increasing the current sensitivity of a galvanometer does not necessarily increase the voltage sensitivity.” Justify this statement. (Comptt. Delhi 2014)
Answer:
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring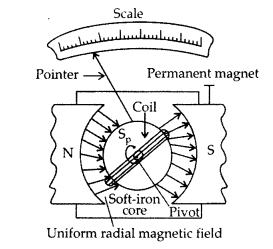
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.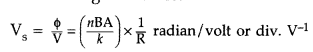
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
Question 67.
A uniform magnetic field \(\overrightarrow{\mathrm{B}}\) is set up along the positive x-axis. A particle of charge ‘q’ and mass ‘m’ moving with a velocity v enters the field at the origin in X-Y plane such that it has velocity components both along and perpendicular to the magnetic field \(\overrightarrow{\mathrm{B}}\). Trace, giving reason, the trajectory followed by the particle. Find out the expression for the distance moved by the particle along the magnetic field in one rotation. (All India 2014)
Answer:
Since the velocity of the particle is inclined to x-axis, thererfore, the velocity has a component along B, this component remains unchanged as the motion along the magnetic field will not be affected by the magnetic field. The motion in a plane perpendicular to B is as before a circular one, thereby producing a helical motion, which is its trajectory.
If r is the radius of the circular path of a particle, then a force of mv2/r, acts perpendicular to the path towards the centre of the circle and is called the centripetal force. If the velocity v is perpendicular to the magnetic field B, the magnetic force is perpendicular to both v and B and acts like a centripetal force. It has a magnitude qvB. Equating the two expressions (for centripetal force)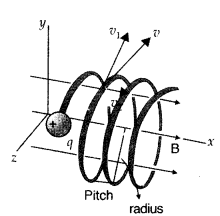
mv2/r = qvB, which gives r = mv/qB …(i) for the radius of the circle described by the charged particle.![]()
There is a component of the velocity parallel to the magnetic field (denoted by v11), it will make the particle move along the field and the path of the particle would be a helical one.
The distance moved along the magnetic field in one rotation is called pitch p.
Using equation (ii), we have![]()
Question 68.
Write the expression for the generalized form of Ampere’s circuital law. Discuss its significance and describe briefly how the concept of displacement current is explained through charging/discharging of a capacitor in an electric circuit. (All India 2014)
Answer:
Maxwell’s displacement current : According to Ampere’s circuital law, the magnetic field \(\overrightarrow{\mathrm{B}}\) is related to steady current I as,![]()
Maxwell showed that this relation is logically inconsistent. He accounted this inconsistency as follows :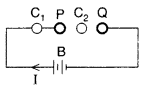
Ampere’s circuital laic for loop C, gives
Loop C2 lies in the region between the plates
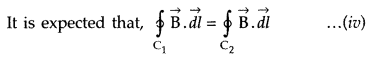
which is logically inconsistent. So, Maxwell gave idea of displacement current.
Thus displacement current is that current which comes into play in the region in which the electric![]()
where [ID is displacement current and![]()
It is now called Ampere-Maxwell law. This is the generalization of Ampere’s Circuital law.
Question 69.
(a) Why is the magnetic field radial in a moving coil galvanometer? Explain how it is achieved.
(b) A galvanometer of resistance ‘G’ can be converted into a voltmeter of range (0 – V) volts by connecting a resistance ‘R’ in series with it. How much resistance will be required to change its range from 0 to V/2? (Comptt. All India 2014)
Answer:
(a) The magnetic field in a moving coil galvanometer is made ‘radial’ to keep the magnetic field ‘normal’ to the area vector of the coil. It is done by taking the cylindrical soft iron core. The torque acting on the coil is maximum (sin θ = 1, when, θ = 90°)
(b) Given : resistance of galvanomter = G Ω
Range of voltmeter (RL) = (0 – V) volts
Resistance to be connected in parallel = R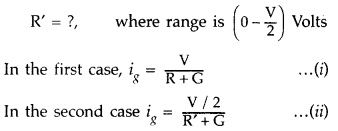
[ig is the maximum current which can flow through galvanometer]
From equation (i) and (ii), on solving we get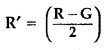
Question 70.
A closely wound solenoid of 2000 turns and cross sectional area 1.6 × 10-4 m2 carrying a current of 4.0 A is suspended through its centre allowing it to turn in a horizontal plane. Find
(i) the magnetic moment associated with the solenoid,
(ii) magnitude and direction of the torque on the solenoid if a horizontal magnetic field of 7.5 × 10-2 T is set up at an angle of 30° with the axis of the solenoid. (Comptt. All India 2014)
Answer: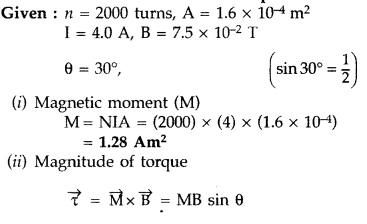
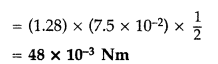
(iii) Direction of torque is perpendicular to both the planes of the solenoid and the magnetic field.
Question 71.
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
(b) A neutron, an electron and an alpha particle moving with equal velocities, enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer. (Delhi 2016)
Answer:
(a) Expression for magnetic force :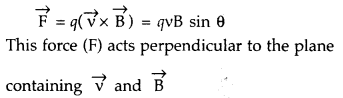
(b) Justification : Direction of force experienced by 01 the particle will be n according to Fleming’s Left hand rule.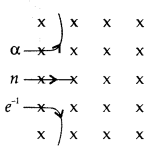
Question 72.
Two long straight parallel conductors carry steady current I1 and I2 separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other. Obtain the expression for this force. Hence define one ampere. (Delhi 2014)
Answer:
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A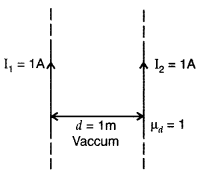
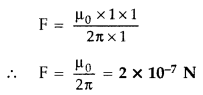
Question 73.
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular . wire carrying current I. (All India 2014)
Answer:
(i) According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.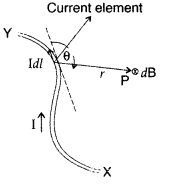

Magnetic field on the axis of circular current loop :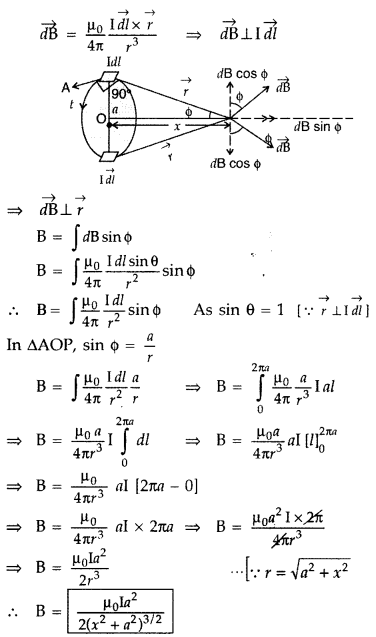
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
(ii)
(a) Magnetic field lines :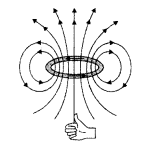
(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.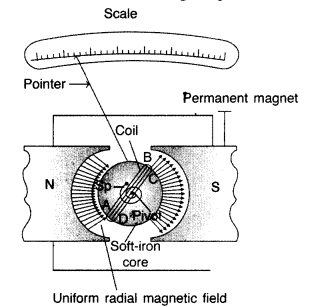
Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.
Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900
Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque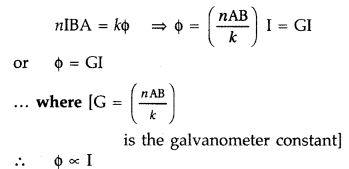
This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.
Question 74.
Three long straight parallel wires are kept as shown in the figure. The wire (3) carries a current I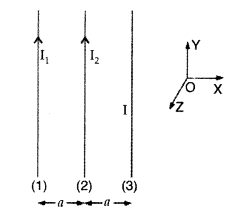
(i) The direction of flow of current I in wire (3), is such that the net force, on wire (1), due to the other two wires, is zero.
(ii) By reversing the direction of I, the net force, on wire (2), due to the other two wires, becomes zero. What will be the directions of current I, in the two cases? Also obtain the relation between the magnitudes of currents I1 I2 and I.
Answer: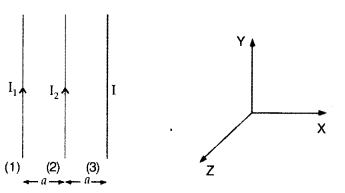
(i) Net force experienced by wire (1) can be zero only, when the current in wire (3) flows along – \(\hat{\mathrm{j}}\) i.e. downwards, it means that the forces acting on wire (1) due to wire (3) and wire (2) are equal and opposite.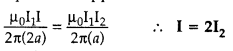
(ii) When direction of current in wire (3) is reversed then current should be along + \(\hat{\mathrm{j}}\) i.e. upwards.
For this case net force on wire (2) becomes zero, which means that the forces due to wire (1) and wire (3) are equal and opposite.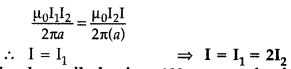
Question 75.
A circular coil, having 100 turns of wire, of radius (nearly) 20 cm each, lies in the XY plane with its centre at the origin of co-ordinates. Find the magnetic field, at the point (0, 0, 20√3 cm), when this coil carries a current of (Comptt. Delhi 2016)
Answer:
Question 76.
Write the expression for the magnetic force \(\overrightarrow{\mathbf{F}}\) acting on a charged particle q moving with velocity \(\overrightarrow{\mathbf{F}}\) in the presence of the magnetic field \(\overrightarrow{\mathbf{B}}\) in a vector form. Show that no work is done and no change in the magnitude of the velocity of the particle is produced by this force. Hence define the unit of magnetic field. (Comptt. All India 2016)
Answer:
(i) The required expression is \(\[\]\overrightarrow{\mathbf{F}}=q(\vec{v} \times \overrightarrow{\mathbf{B}})\)
(ii) The magnetic force, at all instants, is, therefore, perpendicular to the instantaneous direction of \(\vec{v}\), which is also the instantaneous direction of displacement (\(\overrightarrow{d s}\)).
Since, \(\overrightarrow{\mathrm{F}}\) is perpendicular to (\(\overrightarrow{d s}\)), at all instants, work done \((=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{d s})\) is zero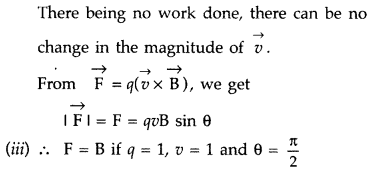
Hence, the magnetic field \(\overrightarrow{\mathrm{B}}\), at a point equals one tesla if a charge of one coulomb, moving with a velocity 1/sec, along a direction perpendicular to the direction of \(\overrightarrow{\mathrm{B}}\), experience a force of one newton.
Question 77.
A long straight wire, of circular cross section (radius = a) carries a current I which is uniformly distributed across the cross section of the wire.
Use Ampere’s circuital law to calculate the magnetic field B(r), due to this wire, at a point distance r < a and r > a from its axis. Draw a graph showing the dependence of B(r) on r. (Comptt. All India 2016)
Answer: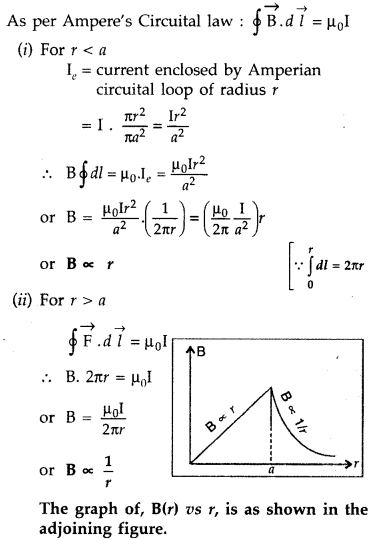
Question 78.
Derive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B. Show that \(\vec{\tau}=\vec{m} \times \overrightarrow{\mathbf{B}}\) where \(\vec{m}\) is the magnetic moment of the current loop given by \(\vec{m}=\overrightarrow{\mathbf{I}} \overrightarrow{\mathbf{A}}\). (Comptt. All India)
Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)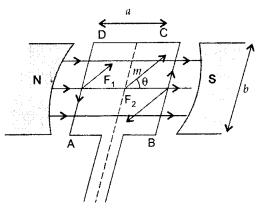
Force exerted on the arm DA inward
F1 = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F2 = I b B ∴ F2 = F1
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,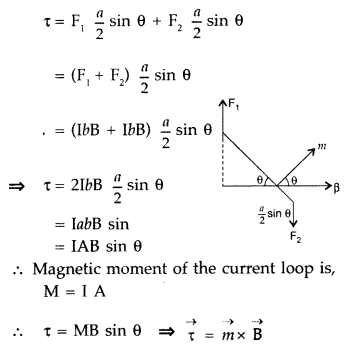
If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.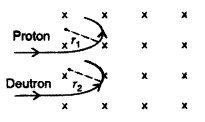
Question 79.
(i) Obtain the expression for the cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency? Give reason to justify your answer. (Delhi 2017)
Answer:
(i) Expression for cyclotron frequency : The magnetic field provides necessary centripetal force needed by the charged particle to move in a circular path.
m = mass of the charged particle,
v = velocity,
r = radius of the circular path
q = charge,
B = Magnetic field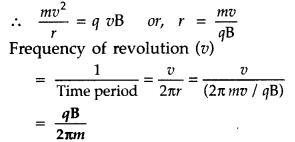
Therefore, the frequency of revolution is independent of energy of the particle.
(ii) The mass of the two particles, i.e. deuteron and proton, is different. Since cyclotron frequency depends inversely on the mass, they cannot be accelerated by the same oscillator frequency.
Question 80.
Describe the working principle of a moving coil galvanometer. Why is it necessary to use
(i) a radial magnetic field and
(ii) a cylindrical soft iron core in a galvanometer? Write the expression for current sensitivity of the galvanometer.
Can a galvanometer as such be used for measuring the current? Explain. (Delhi 2017)
Answer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring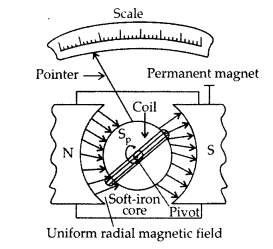
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.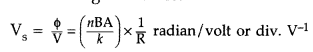
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
No, the galvanometer cannot be used to measure current. It can only detect current but cannot measure as it is not calibrated. The galvanometer coil is likely to be damaged by currents in the (mA/A) range.
Question 81.
An electron of mass me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence prove that the magnetic moment associated with it is expressed as \(\vec{\mu}=-\frac{e}{2 m_{e}} \overrightarrow{\mathbf{L}}\) where L is the orbital angular momentum of the electron. Give the significance of negative sign. (Delhi 2017)
Answer:
(i) Electron, in circular motion around the nucleus, constitutes a current loop which behaves like a tiny magnetic dipole.
Current associated with the revolving electron :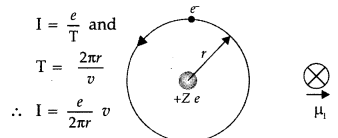
Magnetic moment of the loop, µ = IA
Negative sign signifies that the angular momentum of the revolving electron is opposite in direction to the magnetic moment associated with it.
Question 82.
(a) Write the expression for the force \(\overrightarrow{\mathbf{F}}\) acting on a particle of mass m and charge q moving with velocity \(\overrightarrow{\mathbf{v}}\) in a magnetic field \(\overrightarrow{\mathbf{B}}\). Under what conditions will it move in
(i) a circular path and
(ii) a helical path?
(b) Show that the kinetic energy of the particle moving in magnetic field remains constant. (Delhi 2017)
Answer:![]()
(i) When velocity of charged particle and magnetic field are perpendicular to each other, it will move in a circular path.
(ii) When velocity is neither parallel nor perpendicular to the magnetic field, it will move in helical path.
(b) The force experienced by the charged particle, is perpendicular to the instantaneous velocity \(\vec{v}\), at all instants.
Hence the magnetic force cannot bring any change in the speed of the charged particle. Since speed remains constant, the kinetic energy also stays constant.
Question 83.
(a) State Biot-Savart law and express this law in vector form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils. (All India 2017)
Answer:
(a) Biot-Savart law : It states that “the magnetic field dB due to a current element d l at any point P is:
(i) directly proportional to current dB ∝ I.
(ii) directly proportional to the length dl of the element \(d \vec{B}\) ∝ dl.
(iii) directly proportional to sin θ, where θ is the angle between d\(\overrightarrow{l}\) and \(\overrightarrow{r}\),
Therefore \(d \vec{B}\) ∝ sin θ
(iv) inversely proportional to the square of the distance r from the current element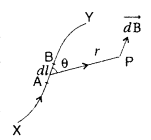
Combining (i), (ii), (iii) and (iv), we get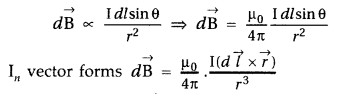
The direction of \(\overrightarrow{d \mathrm{B}}\) is perpendicular to the plane of the vector d \(\vec{l}\) and \(\vec{r}\) given by Right Handed Screw Rule.
(b) Consider a circular coil of radis r, carrying current I. It consists of a large number of small current elements of length dl. According to Biot-Savart law, magnetic field at the centre O due to current element dl is,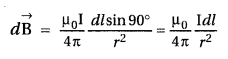
Magnetic field due to all such current elements will point into the plane of paper.
Hence total field at O is,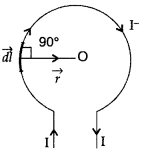
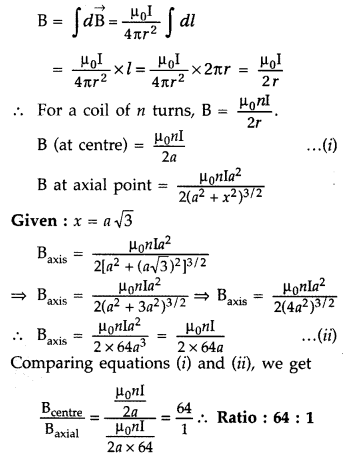
(b) Given : RP = RQ = R, Ip = 1 A, IQ = √3 A
B = ? (Magnitude and direction)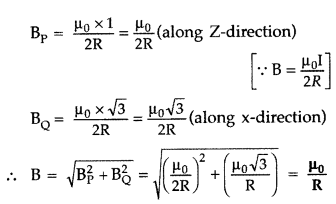
This net magnetic field B, is inclined to the field BP, at an angle θ, where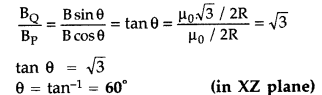
Question 84.
Two identical loops P and Q each of radius 5 cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils, if they carry currents equal to 3 A and 4 A respectively. (All India 2017)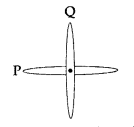
Answer:
Question 85.
State the Lorentz’s force and express it in vector form. Which pair of vectors are always perpendicular to each other? Derive the expression for the force acting on a current carrying conductor of length L in a uniform magnetic field ‘B’. (Comptt. Delhi 2017)
Answer:
Lorentz’s magnetic force is force experienced by a charged particle of charge ‘q’ moving in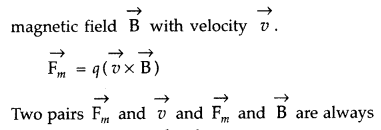
perpendicular to each other Let us consider a conductor of uniform cross-sectional area A and length ‘U having number density of electrons as V Total force on charge carriers in the conductor,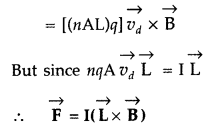
Question 86.
Define the term magnetic moment of a current loop. Derive an expression for the magnetic field at any point along the axis of a solenoid of length 21, and radius «, and number of terms per unit length n. (Comptt. Delhi 2017)
Answer:
(i) Definition of magnetic moment: Magnetic moment of a current loop is equal to the product of current flowing in the loop and its area; and its direction is along area vector as per the right handed screw rule.
(ii) Magnetic field for solenoid :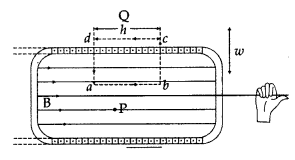
Using Ampere’s circuital law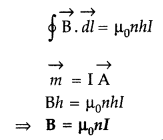
Question 87.
(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical circular loops X and Y of radius R and carrying the same current are kept in perpendicular planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loops. (Comptt. All India 2017)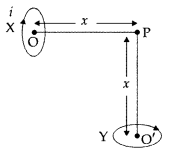
Answer:
(a) Pattern of magnetic field lines for a circular coil carrying current :
(a) Magnetic field lines :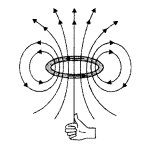
(b) The magnetic field due to a circular coil at a point carrying current is given by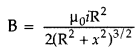
Since these two circular coils are identical and carrying the same current,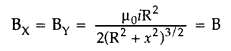
Resultant magnetic field (BR)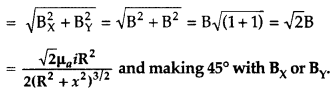
Question 88.
Define the term current sensitivity of a galvanometer. Write its SI unit. (Comptt. All India 2017)
Answer:
• Current sensitivity of a galvanometer is “deflection per unit current”. It is defined as the ratio of deflection produced in the galvanometer to the current flowing through it.![]()
SI unit is radian per ampere.
Question 89.
A toroidal solenoid of mean radius 20 cm has 4000 turns of wire wound on a ferromagnetic core of relative permeability 800. Calculate the magnetic field in the core for a current of 3A , passing through the coil. How does the field change, when this core is replaced by a core of Bismuth? (Comptt. All India 2017)
Answer: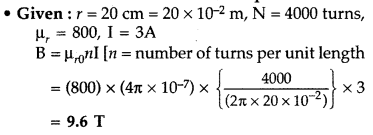
Since bismuth is diamagnetic, its μr < 1, therefore the magnetic field in the core will be very much reduced.
Moving Charges and Magnetism Class 12 Important Questions Long Answer Type
Question 90.
(a) Using Biot-Savart’s law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current i.
(b) Two small identical circular coils marked 1, 2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O. (Delhi 2017)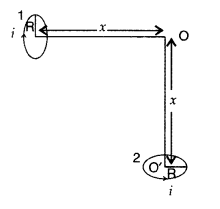
Answer:
(a) Consider a circular loop of wire of radius R carrying current I. The entire loop can be divided into a large number of small current elements.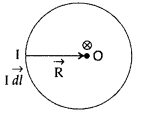
According to Biot-Savart’s law, magnetic field due to current element ‘Idl’ at the centre O of a coil is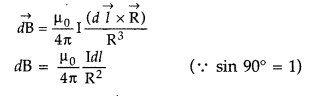
The direction of d \(\vec{l}\) is along the tangent
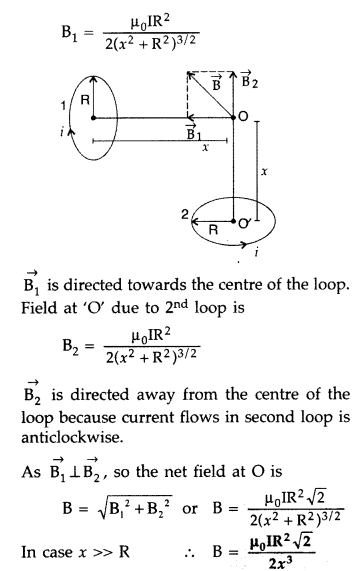
Question 91.
Draw a schematic diagram of a cyclotron. Explain its underlying principle and working, stating clearly the function of the electric and magnetic field applied on a charged particle. Deduce an expression for the period of revolution and show that it does not depend on the speed of the charged particle. (Delhi 2017)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.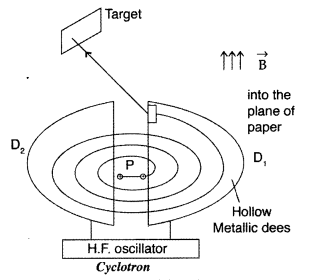
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding
effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
Question 92.
Draw a schematic sketch of a cyclotron. Explain briefly how it works and how it is used to accelerate the charged particles.
(i) Show that time period of ions in a cyclotron is independent of both the speed and radius of circular path.
(ii) What is resonance condition? How is it used to accelerate the charged particles? (All India 2017)
Answer:
(i) Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
(ii) The frequency va of the applied voltage is adjusted so that the polarity of the dees is reversed in the same time that it takes the ions to complete one-half of the revolution. The requirement va = vc is called the resonance condition.
The phase of the supply is adjusted so that when the positive ions arrive at the edge of D1, D2 is at a lower potential and the ions are accelerated across the gap.
Question 93.
(a) Two straight long parallel conductors carry currents I1 and I2 in the same direction. Deduce the expression for the force per unit length between them.
Depict the pattern of magnetic field lines around them.
(b) A rectangular current carrying loop EFGH is kept in a uniform magnetic field as shown in the figure.
(i) What is the direction of the magnetic moment of the current loop?
(ii) When is the torque acting on the loop
(A) maximum,
(B) zero? (All India 2017)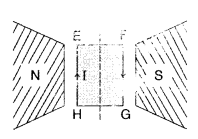
Answer:
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A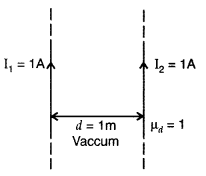
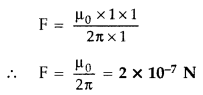
(i) Magnetic moment will be out of the plane from the surface HEFG.
(ii) Torque
(A) Torque is maximum when MII B i.e., when it gets rotated by 90°.
(B) Torque is minimum when M and B are at 270° to each other.
Question 94.
(a) With the help of a diagram, explain the principle and working of a moving coil galvanometer.
(b) What is the importance of a radial magnetic field and how is it produced?
(c) Why is it that while using a moving coil galvanometer as a voltmeter a high resistance in series is required whereas in an ammeter a shunt is used? (All India)
Answer:
(a) Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring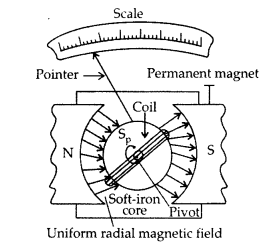
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.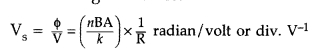
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) For radial magnetic field, sin θ = 1,
so torque τ = NIAB.
Thus when radial magnetic field is used, the deflection of the coil is proportional to the current flowing through it. Hence a linear scale can be used to determine the deflection of the coil.
(c) A high resistance is joined in series with a galvanometer so that when the arrangement (voltmeter) is used in parallel with the selected section of the circuit, it should draw least amount of current. In case voltmeter draws appreciable amount of current, it will disturb the original value of potential difference by a good amount.
To convert a galvanometer into ammeter, a shunt is used in parallel with it so that when the arrangement is joined in series, the maximum current flows through the shunt, and thus the galvanometer is saved from its damage, when the current is passed through ammeter.
Question 95.
(a) Derive an expression for the force between two long parallel current carrying conductors.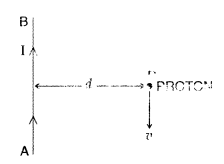
(b) Use this expression to define S.I. unit of current.
(c) A long straight wire AB carries a current I. A proton P travels with a speed v, parallel to the wire, at a distance d from it in a direction opposite to the current as shown in the figure. What is the force experienced by the proton and what is its direction? (All India)
Answer:
(a) For (a) and (b) :
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A
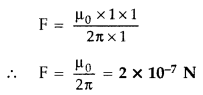
(c) Force experienced by the proton,![]()
As magnetic field due to the current carrying wire is directed into the plane of the paper (θ = 90°)![]()
Force is directed away from the current carrying wire or in the right direction of observer.
Question 96.
State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying current behave as a magnet? (Delhi 2011)
Answer:
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.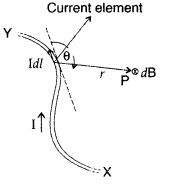
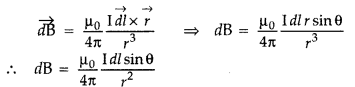
Magnetic field on the axis of circular current loop :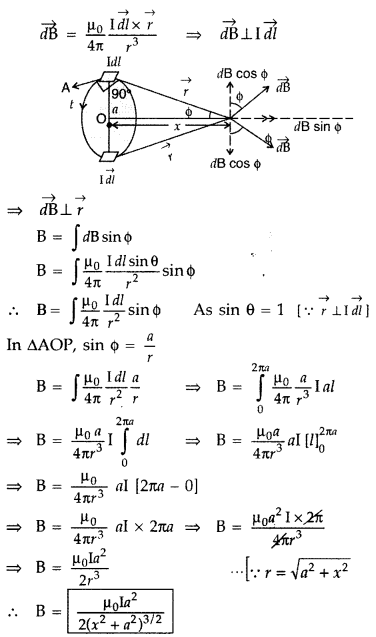
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
Question 97.
With the help of a labelled diagram, state the underlying principle of a cyclotron. Explain clearly how it works to accelerate the charged particles. Show that cyclotron frequency is independent of energy of the particle. Is there an upper limit on the energy acquired by the particle? Give reason. (Delhi 2011)
Answer:
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.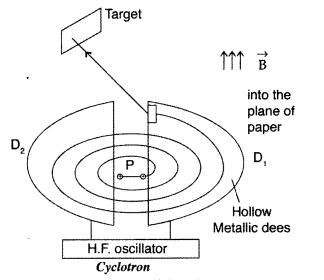
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
Yes, there is an upper limit. The increase in the kinetic energy of particles is qv. Therefore, the radius of their path goes on increasing each time, their kinetic energy increases. The lines are repeatedly accelerated across the dees, untill they have the required energy to have a radius approximately that of the dees. Hence, this is the upper limit on the energy required by the particles due to definite size of dees.
Question 98.
(a) State the principle of the working of a moving coil galvanometer, giving its labelled diagram.
(b) “Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity.” Justify this statement
(c) Outline the necessary steps to convert a galvanometer of resistance RG into an ammeter of a given range. (All India 2011)
Answer:
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring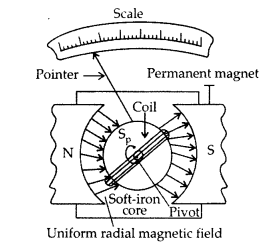
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.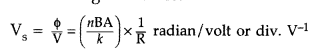
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Since \(\mathrm{v}_{\mathrm{s}}=\frac{\mathrm{I}_{\mathrm{s}}}{\mathrm{R}}\) increase in current sensitivity may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(c) Conversion of galvanometer into ammeter: By just connecting a low resistance known as shunt in parallel to the galvanometer, it can be converted into an ammeter.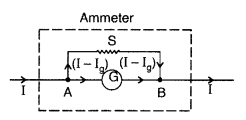
Let G = resistance of the galvanometer.
Ig = the current with which galvanometer gives full scale deflection.
S = shunt resistance
I – Ig = current through the shunt.
As the galvanometer and shunt are connected in parallel,
Potential difference across the galvanometer = Potential difference across the shunt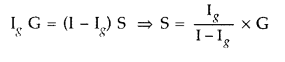
Question 99.
(a) Write the expression for the force, \(\overrightarrow{\mathbf{F}}\), acting on a charged particle of charge ‘q’, moving with a velocity latex]\overrightarrow{\mathbf{v}}[/latex] in the presence of both electric field \(\overrightarrow{\mathrm{E}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\). Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l × b carrying a steady current I is placed in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\). Prove that the torque \(\vec{\tau}\) acting on the loop is given by \(\vec{\tau}=\vec{m} \times \overrightarrow{\mathrm{B}}\), where \(\overrightarrow{\mathrm{m}}\) is the magnetic moment of the loop. (All India 2011)
Answer:
(a) A charge q in an electric field \(\overrightarrow{\mathrm{E}}\) experiences the electric force, \(\overrightarrow{\mathrm{F}}_{e}=q \overrightarrow{\mathrm{E}}\)
This force acts in the direction of field \(\overrightarrow{\mathrm{E}}\) and is independent of the velocity of the charge.
The magnetic force experienced by the charge q moving with velocity \(\overrightarrow{\mathrm{v}}\) in the magnetic field B is given by![]()
This force acts perpendicular to the plane of \(\overrightarrow{\mathrm{V}}\) and \(\overrightarrow{\mathrm{B}}\) and depends on the velocity \(\overrightarrow{\mathrm{v}}\) of the charge.
The total force, or the Lorentz force, experienced by the charge q due to both electric and magnetic field is given by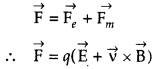
Hence, A stationary charged particle does not experience any force in a magnetic field. (b) Torque on a current loop in a uniform magnetic field.
Let I = Current flowing through the coil PQRS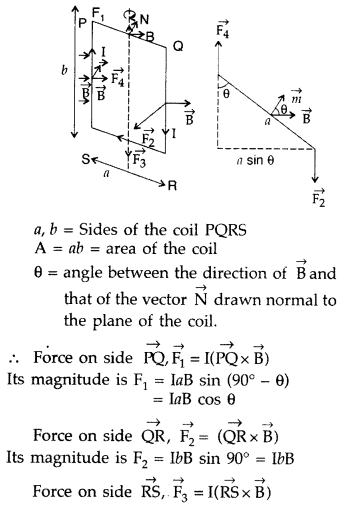
Its magnitude is, F3 = IaB sin(90° + 0)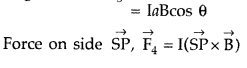

Question 100.
(a) Explain, giving reasons, the basic difference in converting a galvanometer into
(i) a voltmeter and
(ii) an ammeter.
(b) Two long straight parallel conductors carrying steady currents I1 and I2 are separated by a distance’d’ Explain briefly, with the help of a suitable diagram, how the magnetic field due to one conductor acts on the other. Hence deduce the expression for the force acting between the two conductors. Mention the nature of this force.
Answer:
(a) (i) Voltmeter is connected in parallel with the circuit element across which the potential difference is intended to be measured.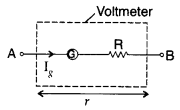
A galvanometer can be converted into a voltmeter by connecting a higher resistance in series with it. The value of this resistance is so adjusted that only current I which produces full scale deflection in the galvanometer, passes through the galvanometer.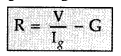
(ii) A galvanometer can be converted into an ammeter by connecting a low value
resistance in parallel with it.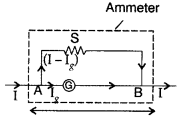
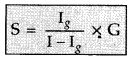
(b)
Consider two infinitely long parallel conductors carrying current I1 and I2 in the same direction.
Let d be the distance of separation between these two conductors.
Hence, force is attractive in nature.
Ampere : Ampere is that current which is if maintained in two infinitely long parallel conductors of negligible cross-sectional area separated by 1 metre in vacuum causes a force of 2 × 10-7 N on each metre of the other wire.
Then current flowing is 1A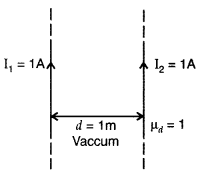
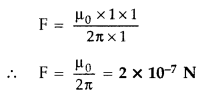
Question 101.
(a) Explain briefly with the help of a labelled diagram, the principle and working of a moving coil galvanometer.
(b) Define the term ‘current sensitivity’ of a galvanometer. How is it that increasing current sensitivity may not necessarily increase its voltage sensitivity? Explain. (Comptt. All India 2011)
Answer:
(a) Principle and working of a moving coil galvanometer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring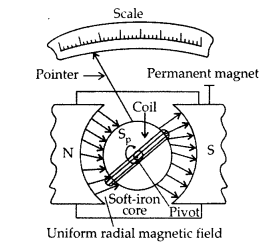
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.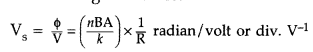
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Current sensitivity:
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.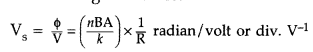
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
Question 102.
(a) State Biot-Savart law. Deduce the expression for the magnetic field due to a circular current carrying loop at a point lying on its axis.
(b) Two long parallel wires carry currents I1 and I2 flowing in the same direction. When a third current carrying wire is placed parallel and coplanar in between the two, find the condition when the third wire would experience no force due to these two wires. (Comptt. All India 2011)
Answer:

The components perpendicular to the axis of the loop will be equal and opposite to component along the axis of the loop and will cancel out. Their axial components will be in the same direction, i.e., along CP and get added up.
∴ Total magnetic field at point P in the direction CP is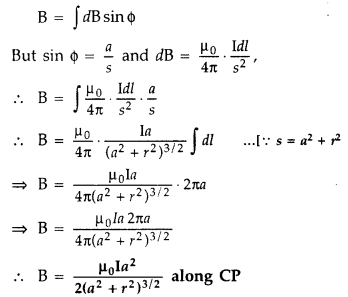
The direction of this field is along the axis, in the sense given by the right hand (thumb) rule.
(b) The force \(\overrightarrow{f_{1}}\) on the third wire due to wire 1 is directed opposite to the force \(\overrightarrow{f_{2}}\) on the third wire due to wire 2. Hence, the net force on the third wire would become 0.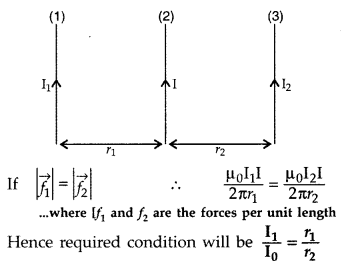
Question 103.
(a) Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
(b) A proton and a deutron having equal momenta enter in a region of uniform magnetic field at right angle to the direction of the field. Depict their trajectories in the field. (Delhi 2013)
Answer:
(a) Torque on a rectangular current loop in a uniform magnetic field:
Let I = current through the coil
a, b – sides of the rectangular loop
A = ab = area of the loop
n = Number of turns in the loop
B = Magnetic field
θ = angle between magnetic field
\(\overrightarrow{\mathrm{B}}\) and area vector \(\overrightarrow{\mathrm{A}}\)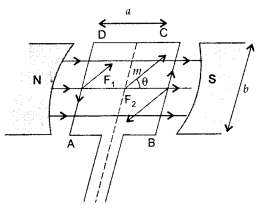
Force exerted on the arm DA inward
F1 = I b B …[∵ F = ILB]
Force exerted on the arm BC outward
F2 = I b B ∴ F2 = F1
Thus net force on the loop is zero
∴ Two equal and opposite forces form a couple which exerts a torque
∴ Magnitude of the torque on the loop is,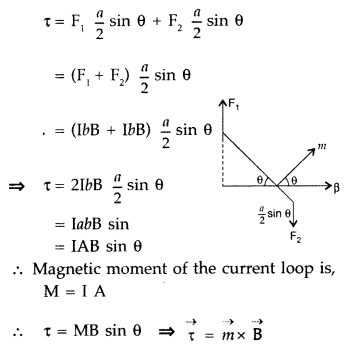
If loop has n turns then M = n I A
∴ τ = nIAB sin θ
When θ = 90° then \(\tau_{\max }=n I A B\)
When θ = 0° then τ = 0
(b) Since the momentum and the charge on both the proton and deutron are the same, the particle will follow a circular path with radius 1:1.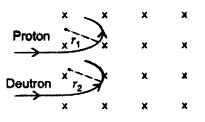
Question 104.
(a) Using Biot-Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero. (All India 2013)
Answer:
(a) Let P be the point on the axis of a circular loop or coil of radius a carrying current I. The distance of P from the centre of loop is x.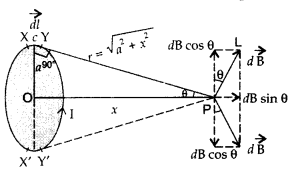
According to Biot-Savart’s Law, magnetic field due to a small element XY (dl) at point P is![]()
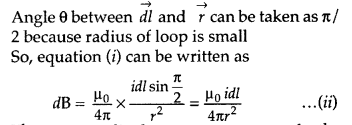
The perpendicular components of the magnetic field due to these elements being equal and opposite cancel each other. Hence the total contribution of perpendicular components, (i.e. dB cos θ) to the net magnetic field is zero.
On the other hand, dB sin θ component of magnetic field due to each element of the coil or loop is directed in the same direction.
Therefore, magnetic field at point P due to the whole coil or loop is equal to the sum of dB sin θ components of magnetic field due to each element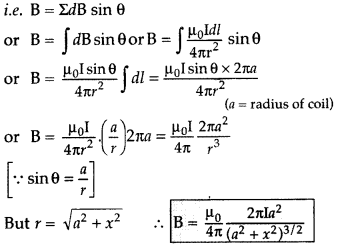
The right hand thumb rule can be used to find the direction of the field.
(b) A toroid is a solenoid bent to form a ring shape.
Let N number of turns per unit length of toroid and I be current flowing in it.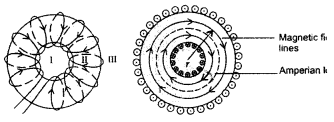
Consider a loop (region II) of radius r passes through the centre of the toroid.
Let (region II) \(\overrightarrow{\mathrm{B}}\) be magnetic field along the loop is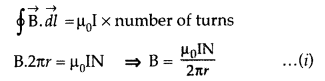
Let (region I) B1 be magnetic field outside toroid in open space. Draw an amperian loop L2 of radius r2 through point Q.
Now applying ampere’s law :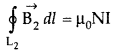
As I = 0, because the circular turn current coming out of plane of paper is cancelled exactly by current going into it, so net I = 0, equation (i) becomes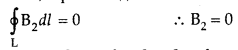
Question 105.
(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence derive the expression for the kinetic energy acquired by the particles.
(b) An α-particle and a proton are realeased from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency? Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees? (All India 2013)
Answer:
(a) Cyclotron :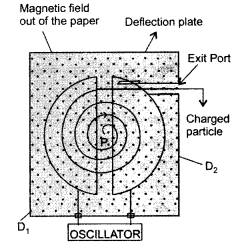
Role of crossed electric and magnetic field in cyclotron : The magnetic field makes the charged particle to cross the gap between the dees again and again by making it move along a circular path, while the oscillating electric field, applied across the dees, accelerates the charged particle again and again and hence increases its K.E.
Expression :
If the velocity v is perpendicular to the magnetic field B, the magnetic force is perpendicular to both v and B and acts like a centripetal force. It has a magnitude qvB. Equating the two expressions for centripetal force,
No, both cannot be accelerated to same frequency because frequency depends upon mass and charge.
(ii) Velocity is given by the formula v = \(\frac{B q r}{m}\)
Velocity is also inversely proportional to mass and directly proportional to charge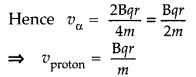
Velocity of proton is higher than that α-particle.
Question 106.
State Biot-Savart law, expressing it in the vector form. Use it to obtain the expression for the magnetic field at an axial point, distance ‘d’ from the centre of a circular coil of radius V carrying current T. Also find the ratio of the magnitudes of the magnetic field of this coil at the centre and at an axial point for which
d = a√3. (Comptt. Delhi 2013)
Answer:
(a) Biot-Savart law : It states that “the magnetic field dB due to a current element d l at any point P is:
(i) directly proportional to current dB ∝ I.
(ii) directly proportional to the length dl of the element \(d \vec{B}\) ∝ dl.
(iii) directly proportional to sin θ, where θ is the angle between d\(\overrightarrow{l}\) and \(\overrightarrow{r}\),
Therefore \(d \vec{B}\) ∝ sin θ
(iv) inversely proportional to the square of the distance r from the current element![]()
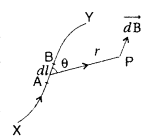
Combining (i), (ii), (iii) and (iv), we get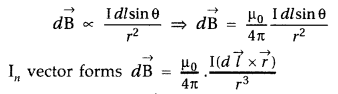
The direction of \(\overrightarrow{d \mathrm{B}}\) is perpendicular to the plane of the vector d \(\vec{l}\) and \(\vec{r}\) given by Right Handed Screw Rule.
(b) Consider a circular coil of radis r, carrying current I. It consists of a large number of small current elements of length dl. According to Biot-Savart law, magnetic field at the centre O due to current element dl is,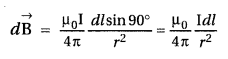
Magnetic field due to all such current elements will point into the plane of paper.
Hence total field at O is,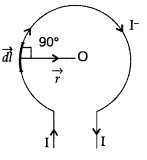
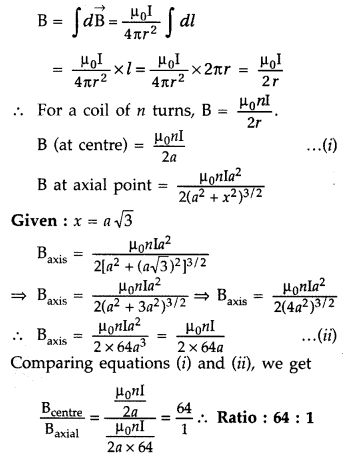
Question 107.
(a) Draw the magnetic field lines due to a current carrying loop.
(b) State using a suitable diagram, the working principle of a moving coil galvanometer. What is the function of a radial magnetic field and the soft iron core used in it?
(c) For converting a galvanometer into an ammeter, a shunt resistance of small value is used in parallel, whereas in the case of a voltmeter a resistance of large value is used in series. Explain why. (Comptt. Delhi 2011)
Answer:
(a) Magnetic field lines :
(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.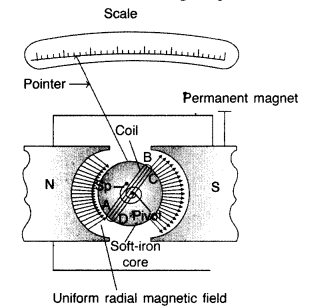
Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.
Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900
Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque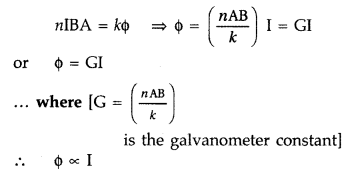
This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.
Question 108.
(a) Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
(b) Draw a schematic sketch of a cyclotron. Explain, giving the essential details of its construction, how it is used to accelerate the charged particles. (All India 2011)
Answer:
(a) When a charged particle with charge q moves inside a magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity v, it experiences a force, which is given by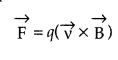
Here, \(\overrightarrow{\mathrm{v}}\) is perpendicular to \(\overrightarrow{\mathrm{B}}\), \(\overrightarrow{\mathrm{F}}\) is the force on the charged particle which acts as the centripetal force and makes it move along a circular path.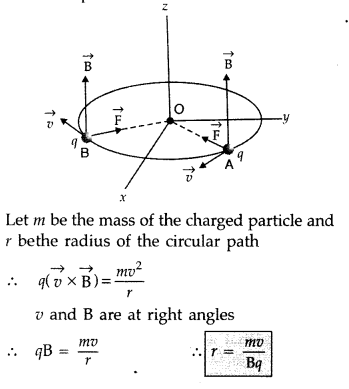
Let m be the mass of the charged particle and r be the radius of the circular path.
Time period of circular motion of the charged particle can be calculated as shown below:
Therefore, the frequency of the revolution of the charged particle is independent of the velocity or the energy of tire particle.
(b) Cyclotron.
Principle : When a positively charged particle is made to move again and again in a high frequency electric field, it gets accelerated and acquires sufficiently large amount of energy.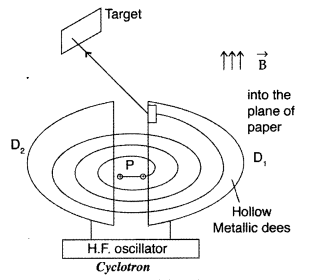
Working : Suppose a positive ion, say a proton, enters the gap between the two dees and finds dee D1 to be negative. It gets accelerated towards dee D1. As it enters the dee D1, it does not experience any electric field due to shielding effect of the metallic dee. The perpendicular magnetic field throws it into a circular path.
At the instant the proton comes out of dee D1. It finds dee D1 positive and dee D2 negative. It now gets accelerated towards dee D2. It moves faster through dee D2 describing a larger semicircle than before. Thus if the frequency of the applied voltage is kept exactly the same as the frequency of the revolution of the proton, then everytime the proton reaches the gap between the two dees, the electric field is reversed and proton receives a push and finally it acquires very high energy. This proton follows a spiral path. The accelerated proton is ejected through a window by a deflecting voltage and hits the target.
Centripetal force is provided by magnetic field to charged particle to move in a circular back.
Question 109.
(a) Draw a labelled diagram of a moving coil galvanometer. Describe briefly its principle and working.
(b) Answer the following :
(i) Why is it necessary to introduce a cylindrical soft iron core inside the coil of a galvanometer?
(ii) Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity. Explain, giving reason. (All India 2011)
Answer:
(a) Moving coil galvanometer.
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring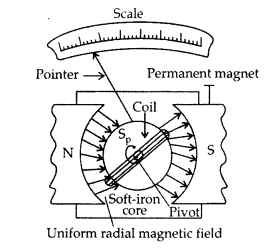
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.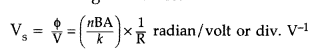
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) (i) Iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(ii) Current sensitivity and voltage sensitivity.
(a)
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.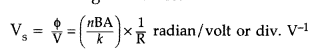
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
(b) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
may not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
Question 110.
(a) State Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius r, having ‘n’ turns per unit length and carrying a steady current I.
(b) 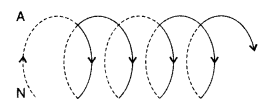
An observer to the left of a solenoid of N turns each of cross section area ‘A’ observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment m = NIA. (Delhi 2011)
Answer:
(a) (i) Ampere’s Circuital Law. Line integral of magnetic field over a closed loop is equal to |i0 times the total current passing through the surface enclosed by the loop. Alternatively![]()
(ii) Expression for magnetic field inside toroid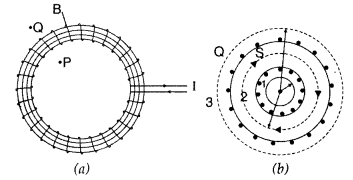
Let the current flowing through each turn of the toroid be I. The total number of turns equals n(2nr) where n is the number of turns per unit length. Applying Ampere’s circuital law, for the Amperian loop, for interior points.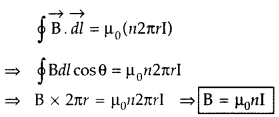
This is the expression for magnetic field inside air-cored toroid.
(b)
(i)Depiction of magnetic field for a solenoid.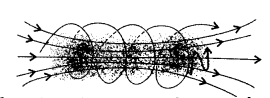
(ii) The solenoid contains N loops, each carrying a current I. Therefore, each loop acts as a magnetic dipole. The magnetic moment for a current I, flowing in loop of area (vector) A is given by, m = IA. The magnetic moments of all loops are aligned along the same direction.
Hence, net magnetic moment equals NIA.
Question 111.
Explain, using a labelled diagram, the principle and working of a moving coil galvanometer.
(a) What is the function of
(i) uniform radial magnetic field,
(ii) soft iron core?
(b)Define the terms
(i) current sensitivity and
(ii) voltage sensitivity of a galvanometer. Why does increasing the current sensitivity not necessarily increase voltage sensitivity? (All India 2011)
Answer:
Principle : “If a current carrying coil is freely suspended/pivoted in a uniform magnetic field, it experiences a deflecting torque.”
Working: As the pivoted coil is placed in a radial magnetic field, hence on passing current I through it, a deflecting torque acts on the coil which is given by, τ = NAIB![]()
The spring Sp attached to the coil provides the counter torque and in equilibrium state balances the deflecting torque. If φ is steady angular deflection then counter torque is kφ.
…where [k = torsional constant of the spring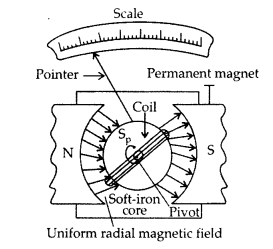
In equilibrium state,![]()
Thus, deflection is directly proportional to the current flowing in the coil.
(a) (i) Uniform radial magnetic field. It keeps the magnetic field line normal to the area vector of the coil.
(ii) Soft iron core in galvanometer. The cylindrical soft iron core, when placed inside the coil of a galvanometer, makes the magnetic field stronger and radial in the space between it and pole pieces, such that whatever the position of the rotation of the coil may be, the magnetic field is always parallel to its plane.
(b) (i) Current sensitivity is defined as the deflection produced in the galvanometer when unit current is passed through its coil.
(ii) Voltage sensitivity is defined as the deflection produced in the galvanometer when unit voltage is applied across the coil of the galvanometer.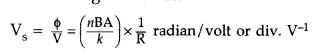
…where [R = Resistance of the coil![]()
does not necessarily increase the voltage sensitivity. It may be affected by the resistance used.
Question 112.
(a) Write, using Biot-Savart law, the expression for the magnetic field \(\overrightarrow{\mathrm{B}}\) due to an element d\(\overrightarrow{\mathrm{l}}\) carrying current I at a distance r from it in a vector form.
Hence derive the expression for the magnetic field due to a current carrying loop of radius R at a point P distant x from its centre along the axis of the loop.
(b) Explain how Biot-Savart law enables one to express the Ampere’s circuital law in the integral form, viz.,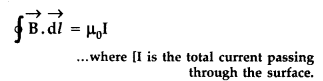 (All India 2011)
(All India 2011)
Answer:
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.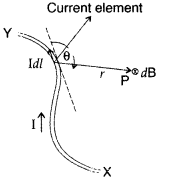
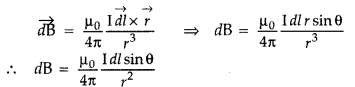
Magnetic field on the axis of circular current loop :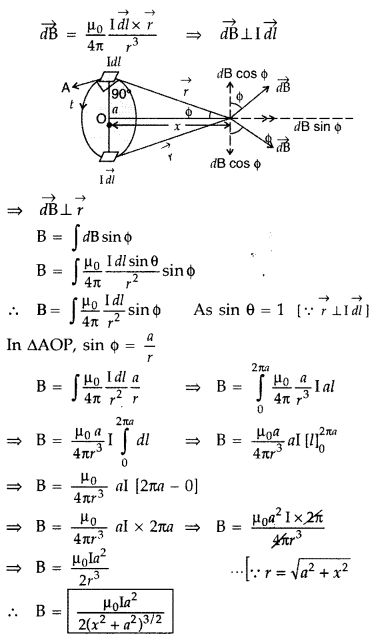
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
(b) Biot-Savart law can be expressed as Ampere’s Circuital law by considering the surface to be made up of a large number of loops. The sum of the tangential components of the magnetic field multiplied by the length of all such elements leads to integral. Ampere’s circuital law states that this’ integral is equal to p0 times the total current passing through that surface, i.e.,![]()
Question 113.
(a) Use Biot-Savart law to derive the expression for the magnetic field due to a circular coil of radius R having N turns at a point on the axis at a distance V from its centre. Draw the magnetic field lines due to this coil.
(b) A current ‘I’ enters a uniform circular loop of radius ‘R’ at point M and flows out at N as shown in the figure.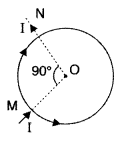
Obtain the net magnetic field at the centre of the loop. (Comptt. Delhi 2011)
Answer:
(a) Biot-Savart Law to derive expression of magnetic field.
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.
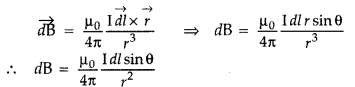
Magnetic field on the axis of circular current loop :
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
Magnetic field lines due to circular coil.
(a) Magnetic field lines :
(b) Moving coil galvanometer. It is a device used for the detection and measurement of small electric current.
Principle. The working is based on the fact that a current carrying coil suspended in a magnetic field experiences a torque.
Construction. It consists of a coil having a large number of turns of insulated copper wire wound on a metallic frame. The coil is suspended by means of a phosphor-bronze strip and is surrounded by a horse-shoe magnet NS. A hair spring is attached to lower end of the coil. The other end of the spring is attached to the scale through a pointer.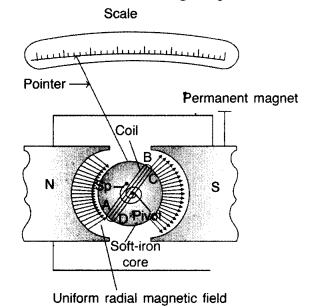
Working. When current is passed, say along ABCD, the couple acts on it. Since the plane remains always parallel to the magnetic field in all positions of the coil (radial field), the force on the vertical arms always remains perpendicular to the place of the coil.
Let, I be the current flowing through coil,
B be magnetic field supposed to be uniform and always parallel to the coil, A be area of the coil
Deflecting torque acting on the coil is,
τ = nI BA sin 900
Due to deflecting torque, the coil rotates and suspension wire gets twisted. A restoring torque is set up in the suspension fibre. If <|) is angle through which the coil rotates and k is the restoring torque per unit angular twist, then restoring torque, τ = kϕ
In equilibrium,
Deflecting torque = Restoring torque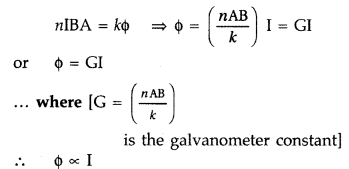
This provide a linear scale for the galvanometer.
Function of a radial magnetic field : Radial magnetic field being normal in all directions is formed to get maximum torque.
Function of Soft iron core, which not only makes the field radial but also increases the strength of the magnetic field.
(c) One uses a shunt resistance in parallel with the galvanometer, so that most of the current passes through the shunt. In the case of a voltmeter, a resistance of large value is used in series because it must draw a very small current, otherwise the voltage measurement will disturb the original set up by an amount which is very large.
(b) Let current I be divided at
point M into two parts I1 and I2; in bigger and smaller parts of the loop respectively. Magnetic field of current (clockwise) at point O :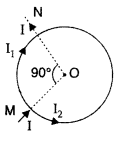
Magnetic field of current I2 (anticlockwise) at point O :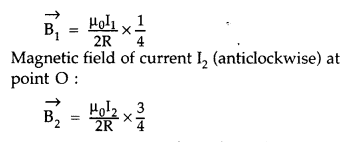
Net magnetic field, \(\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}_{1}}+\overrightarrow{\mathrm{B}_{2}}\)
But I1 = 3I2 (AS resistance of bigger part is three times that of the smaller part of the loop)
Substituting I1 = 3I2 in equation (i), we get![]()
∴ Magnetic field at the centre of loop is zero.
Question 114.
(a) Show how Biot-Savart law can be alternatively expressed in the form of Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside a solenoid of length ‘l’, cross-sectional area ‘A’ having ‘N’ closely wound turns and carrying a steady current ‘I’.
Draw the magnetic field lines of a finite solenoid carrying current I.
(b) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
Find the magnitude and direction of the magnetic field which should be set up in (Comptt. Delhi 2011)
Answer:
(a) (i) Bio-Savart law and Ampere’s Circuital law.
According to Biot-Savart’s law, “magnetic field acting at a particular point due to current carrying element is proportional to the division of cross product of current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated”.
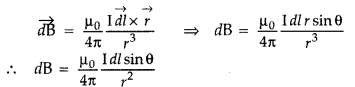
Magnetic field on the axis of circular current loop :
As in a special case we may obtain the field at the centre of the loop. Here x = 0, and we obtain![]()
In a current loop, both the opposite faces behave as opposite poles, making it a magnetic dipole. One side of the current carrying coil behaves like the N-pole and the other side as the S-pole of a magnet.
(b) Biot-Savart law can be expressed as Ampere’s Circuital law by considering the surface to be made up of a large number of loops. The sum of the tangential components of the magnetic field multiplied by the length of all such elements leads to integral. Ampere’s circuital law states that this’ integral is equal to p0 times the total current passing through that surface, i.e.,![]()
(ii) Expression for magnetic field inside a solenoid. Let ‘n’ be the number of turns per unit length. Then total number of turns in the length ‘h’ is nh.
Hence, total enclosed current = nhl
Using Ampere’s circuital law,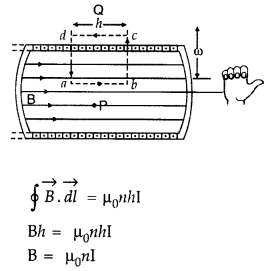
(iii) Magnetic field lines of a finite solenoid
(b) As per the figure given, magnetic field must be vertically inwards, to make tension zero.
Therefore, force on current carrying conductor and the weight of conductor are equal and opposite; and balance each other.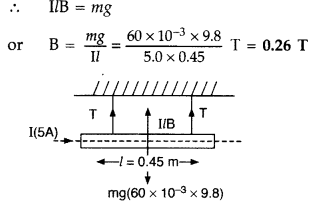
Direction : Perpendicular to the direction of