Question
A student uses a load to pull a box up a ramp inclined at 30°. A string of constant length
and negligible mass connects the box to the load that falls vertically. The string passes
over a pulley that runs on a frictionless axle. Friction acts between the base of the box and
the ramp. Air resistance is negligible.
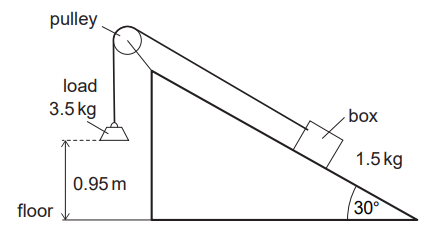
The load has a mass of 3.5kg and is initially 0.95m above the floor. The mass of the box is 1.5kg.
The load is released and accelerates downwards.
(a) Outline two differences between the momentum of the box and the momentum of
the load at the same instant. [2]
(b) The vertical acceleration of the load downwards is 2.4ms-2.
Calculate the tension in the string. [2]
(c) (i) Show that the speed of the load when it hits the floor is about 2.1ms-1. [2]
(ii) The radius of the pulley is 2.5 cm. Calculate the angular speed of rotation of the
pulley as the load hits the floor. State your answer to an appropriate number of
significant figures. [2]
(d) After the load has hit the floor, the box travels a further 0.35m along the ramp before
coming to rest. Determine the average frictional force between the box and the surface
of the ramp. [4]
(e) The student then makes the ramp horizontal and applies a constant horizontal force
to the box. The force is just large enough to start the box moving. The force continues
to be applied after the box begins to move.
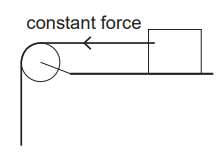
Explain, with reference to the frictional force acting, why the box accelerates once
it has started to move. [3]
Answer/Explanation
Ans.
(a) direction of motion is different / OWTTE $\checkmark$
$m v / m a g n i t u d e$ of momentum is different «even though $v$ the same» $\checkmark$
(b) use of $m a=m g-T « 3.5 \times 2.4=3.5 g-T »$
OR
$
T=3.5(\mathrm{~g}-2.4) \quad \checkmark
$
$
26 « N » \checkmark
$
(c)(i) proper use of kinematic equation $\checkmark$
$
\sqrt{(2 \times 2.4 \times 0.95)}=2.14 \ll \mathrm{m} \mathrm{s}^{-1} » \checkmark
$
(c)(ii) use of $\omega=\frac{v}{r}$ to give 84 «rad $\mathrm{s}^{-11}$
OR
$\omega=2.1 / 0.025$ to give 84 «rad $\mathrm{s}^{-1} » \quad \checkmark$
quoted to 2 sf only $\checkmark$.
(d) ALTERNATIVE 1
$\ll v^2=u^2+2 a s \Rightarrow 0=2.1^2-2 a \times 0.35 »$ leading to $a=6.3 \ll \mathrm{m} \mathrm{s}^{-2} »$
OR
” $x=1 / 2(u+v) t$ ” leading to $t=0.33$ « $s$ ” $\checkmark$
$F_{\text {net }}=« m a=1.5 \times 6.3=» 9.45 « \mathrm{N} » \checkmark$
Weight down ramp $=1.5 \times 9.8 \times \sin (30)=7.4 « \mathrm{~N} » \checkmark$
friction force $=$ net force $-$ weight down ramp $=2.1 « \mathrm{~N} \checkmark$
ALTERNATIVE 2
kinetic energy initial $=$ work done to stop $0.5 \times 1.5 \times(2.1)^2=F_{\text {NET }} \times 0.35 \checkmark$ $F_{\text {net }}=9.45 \ll N » \checkmark$
Weight down ramp $=1.5 \times 9.8 \times \sin (30)=7.4 « \mathrm{~N} » \checkmark$
friction force $=$ net force $-$ weight down ramp $=2.1 « \mathrm{~N} »$
(e) static coefficient of friction $>$ dynamic/kinetic coefficient of friction $/ \mu_{\mathrm{s}}>\mu_{\mathrm{k}} \checkmark$
«therefore» force of dynamic/kinetic friction will be less than the force of static friction $\checkmark$
there will be a net / unbalanced forward force once in motion «which results in acceleration»
OR
reference to net $F=m a$