Question
The Rotor is an amusement park ride that can be modelled as a vertical cylinder of inner radius R rotating about its axis. When the cylinder rotates sufficiently fast, the floor drops out
and the passengers stay motionless against the inner surface of the cylinder. The diagram shows a person taking the Rotor ride. The floor of the Rotor has been lowered away from the person
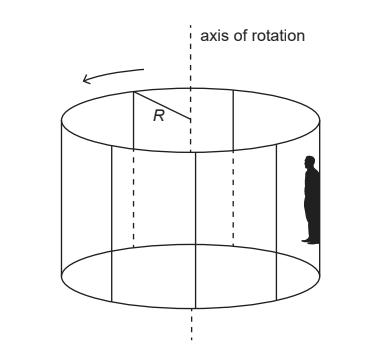
(a) Draw and label the free-body diagram for the person. [2]

(b) The person must not slide down the wall. Show that the minimum angular velocity ω of
the cylinder for this situation is
ω =
where ω is the coefficient of static friction between the person and the cylinder. [2]
(c) The coefficient of static friction between the person and the cylinder is 0.40. The radius
of the cylinder is 3.5 m. The cylinder makes 28 revolutions per minute. Deduce whether
the person will slide down the inner surface of the cylinder. [3]
Answer/Explanation
Ans:
a. arrow downwards labelled weight/W/mg and arrow upwards labelled friction/F arrow horizontally to the left labelled «normal» reaction/N

b. See F N = μ AND N mR = ω2«substituting for N» ω2m R mg =
c.
ALTERNATIVE 1
minimum required angular velocity « = \(\sqrt{\frac{9.81}{0.40\times 3.5}}\) » = 2.6 «rad s-1» actual angular velocity « \(\frac{2\pi }{(\frac{60}{28})}\) 2.9 « = 2.9 «rad s-1»
actual angular velocity is greater than the minimum, so the person does not slide ✓
ALTERNATIVE 2
minimum friction force = mg = «9.81m » actual friction force « = μmRω2 = 0.40 m ×3.5 \((2\pi \frac{28}{60})^2\) » = 12.0 m
actual friction force is greater than the minimum frictional force so the person does not slide