Question
Airboats are used for transport across a river. To move the boat forward, air is propelled from
the back of the boat by a fan blade.

(a) Outline why a force acts on the airboat due to the fan blade. [3]
(b) In a test the airboat is tied to the river bank with a rope normal to the bank. The fan
propels the air at its maximum speed. There is no wind.
(i) Show that a mass of about 240kg of air moves through the fan every second. [2]
(ii) Show that the tension in the rope is about 5kN. [1]
(c) The rope is untied and the airboat moves away from the bank. The variation with time t
of the speed v of the airboat is shown for the motion.
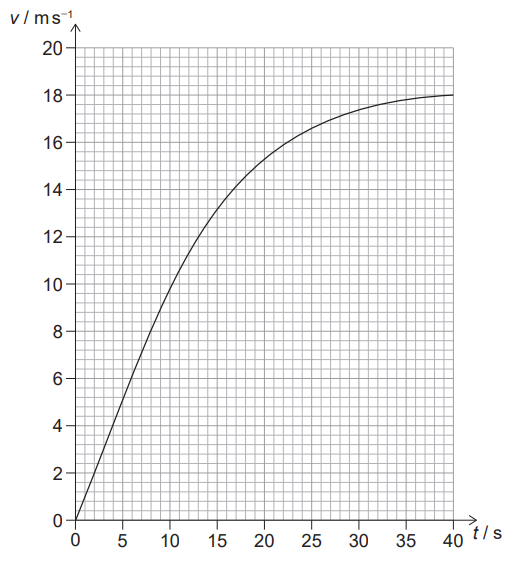
(i) Estimate the distance the airboat travels to reach its maximum speed. [2]
(ii) Deduce the mass of the airboat. [3]
(d) The fan is rotating at 120 revolutions every minute. Calculate the centripetal
acceleration of the tip of a fan blade. [2]
Answer/Explanation
Ans.
(a) ALTERNATIVE 1
there is a force «by the fan» on the air / air is accelerated «to the rear» $\checkmark$ by Newton $3 \checkmark$
there is an «equal and» opposite force on the boat $\checkmark$
ALTERNATIVE 2
air gains momentum «backward» $\checkmark$
by conservation of momentum / force is rate of change in momentum $\checkmark$ boat gains momentum in the opposite direction $\checkmark$
(b)(i) $\pi R^2 O R$ «mass of air through system per unit time $= A v \rho$ seen $\checkmark$
$244 \mathrm{kg} \mathrm{s}^{-1} \checkmark$
(b)(ii) «force $=$ Momentum change per sec $=A v^2 \rho=» 244 \times 20$ OR $4.9 « \mathrm{kN} » \checkmark$
(c)(i)recognition that area under the graph is distance covered $\checkmark$
«Distance $=» 480-560$ «m» $\checkmark$
(c)(ii)calculation of acceleration as gradient at $t=0 \ll=1 \mathrm{~m} \mathrm{~s}^{-2} \mathrm{\|} \checkmark$
use of $F=$ ma OR $\frac{4900}{1}$ seen $\checkmark$
$4900 \pi \mathrm{kg} » \checkmark$
(d) ALTERNATE 1
« $\omega=» 4 \pi \mathrm{rad} \mathrm{s}^{-1} \checkmark$
« $a=r \omega^2=» 280 \ll \mathrm{m} \mathrm{s}^{-2} \| \quad \checkmark$
ALTERNATE 2
$
\begin{aligned}
& 《 v=\frac{2 \pi r}{T} »=22.6 \mathrm{~m} \mathrm{~s}^{-1} \checkmark \\
& 《 a=\frac{v^2}{r} »=280 \ll \mathrm{m} \mathrm{s}^{-2} » \\
&
\end{aligned}
$