Question
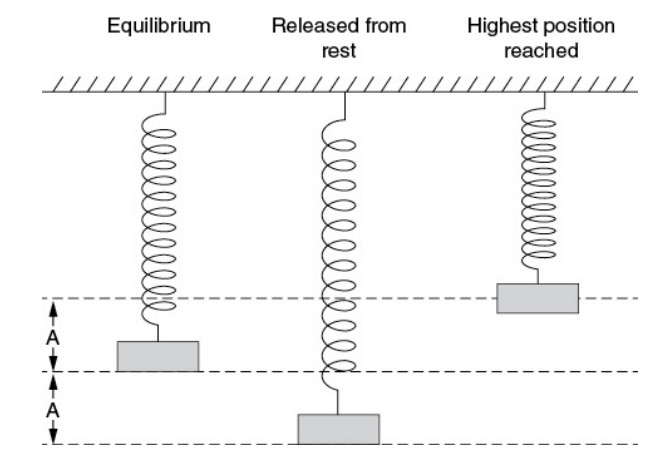
A block is attached to a vertical spring. The block is pulled down a distance A from equilibrium, as shown above, and released from rest. The block moves upward; the highest position above equilibrium reached by the mass is less than A, as shown. When the mass returns downward, how far below the equilibrium position will it reach?
(A) Greater than the distance A below equilibrium
(B) Less than the distance A below equilibrium
(C) Equal to the distance A below equilibrium
(D) No distance—the block will fall only to the equilibrium position.
▶️Answer/Explanation
Ans:B
If friction and air resistance are negligible, a mass on a spring oscillates about the equilibrium position, reaching the same maximum distance above and below. In this case, since the mass doesn’t get all the way to position A at the top, mechanical energy was lost (to friction or air resistance or some nonconservative force). Thus, without some external energy input, the mass won’t reach its maximum position at the bottom, either—at the bottom it will have no kinetic energy, so all the energy will be potential, and we’ve already established that some total mechanical energy was lost.
Question
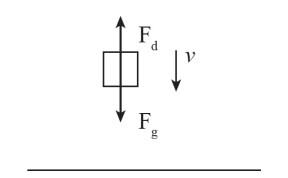
Which of the following correctly describes the motion of a real object in free fall? Assume that the object experiences drag force proportional to speed and that it strikes the ground before reaching terminal speed.
(A) It will fall with increasing speed and increasing acceleration.
(B) It will fall with increasing speed and decreasing acceleration.
(C) It will fall with decreasing speed and increasing acceleration.
(D) It will fall with decreasing speed and decreasing acceleration.
▶️Answer/Explanation
Ans:B
An object’s terminal speed is the highest speed it can reach in free fall. If it has not yet reached that speed, its speed must still be increasing. This eliminates (C) and (D). The problem says that the object will experience a drag force that increases as speed increases. Therefore, the opposing force will increase over time, which means the net force will decrease (since the force from gravity will be constant). If net force decreases, so will acceleration.
Question

Two balls collide as shown above. Given the final direction of the second ball’s motion after the collision, which of the following is a possible direction for the first ball to move after the collision?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
▶️Answer/Explanation
Ans:D
In any collision, the total momentum of the system must be conserved. Prior to the collision, you see that all of the momentum is horizontal. Therefore, the net momentum after the collision must also be purely horizontal. If one ball is moving up after the collision, the other must be moving down to cancel out that vertical momentum.
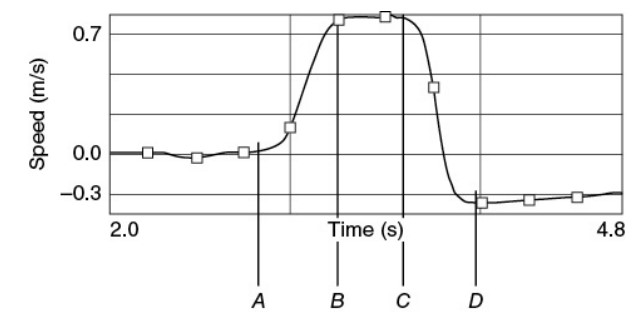
Questions (a) and (b) refer to the following information:
A student pushes cart A toward a stationary cart B, causing a collision. The velocity of cart A as a function of time is measured by a sonic motion detector, with the resulting graph shown in the figure.
Question(a)
At which labeled time did the collision begin to occur?
(A) A
(B) B
(C) C
(D) D
▶️Answer/Explanation
Ans:C
The graph represents the speed of cart A, the one that’s initially moving. So right before the collision, the vertical axis of the graph must be nonzero. Right after the collision, the vertical axis must quickly either decrease or perhaps become negative if the cart changed directions. That’s what happens in the tenth of a second or so after the time labeled C.
