2021-Nov-Physics_paper_1__TZ0_HL – All Questions with detailed solution
Q.1.2021-Nov-Physics_paper_1__TZ0_HL
Topic: Uncertainties and errors
Given: A ball of mass (50 ± 1)g is moving with a speed of (25 ± 1)ms-1.
Calculate: What is the fractional uncertainty in the momentum of the ball?
A. 0.02
B. 0.04
C. 0.06
D. 0.08
Answer/Explanation
Solution
Q.2.2021-Nov-Physics_paper_1__TZ0_HL
Topic: Motion
Given: The graph shows the variation with time t of the velocity of an object.
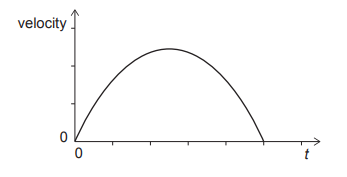
Calculation: What is the variation with time t of the acceleration of the object?
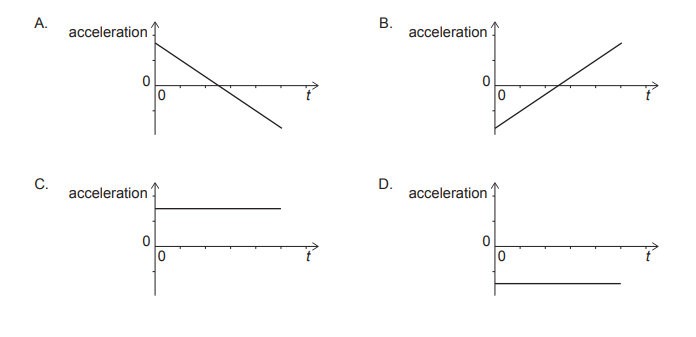
Answer/Explanation
Solution:
$\begin{aligned} & v \propto-t^2 \\ & \frac{d v}{d t} \propto-2 t \\ & a \propto-2 t\end{aligned}$
Q.3.2021-Nov-Physics_paper_1__TZ0_HL
Topic: Forces
Given: X and Y are two objects on a frictionless table connected by a string. The mass of X is 2kg and the mass of Y is 4kg. The mass of the string is negligible. A constant horizontal force of 12N acts on Y.
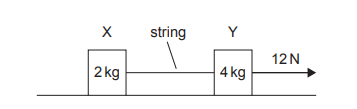
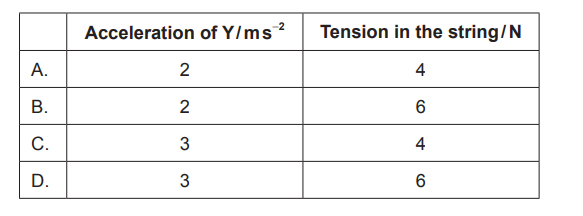
Calculate: What are the acceleration of Y and the magnitude of the tension in the string?
Answer/Explanation
Solution:
$\text{a}=\frac{\mathrm{F}_{\text{net}}}{\text{moving mass}}$
$\text{a}=\frac{12}{6}$
$\mathrm{a}_\text{Y}=2 \mathrm{ms}^{-2}$
$\text{Tension}= 2\times \mathrm{a}$
Q.4.2021-Nov-Physics_paper_1__TZ0_HL
Topic: Work, energy and power
Given: A net force F acts on an object of mass m that is initially at rest. The object moves in a straight line. The variation of F with the distance s is shown.
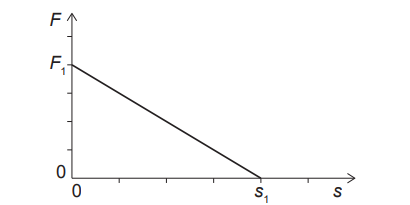
Calculate: What is the speed of the object at the distance s1?
A. $\sqrt{\frac{F_1 ~s_1}{2 m}}$
B. $\sqrt{\frac{F_1~ s_1}{m}}$
C. $\sqrt{\frac{2 F_1~ s_1}{m}}$
D. $\sqrt{\frac{4 F_1~ s_1}{m}}$
Answer/Explanation
Solution:
Area Under $\text{F-s graph}$ Will give change in kinetic energy.
$V_i=o$ (at rest)
$\frac{1}{2} \times F_1 \times S_1=\frac{1}{2} m\left(V_f\right)^2$
Q.5.2021-Nov-Physics_paper_1__TZ0_HL
Topic: Work, energy and power
Given: A cyclist rides up a hill of vertical height 100m in 500s at a constant speed. The combined mass of the cyclist and the bicycle is 80kg. The power developed by the cyclist is 200W.
Calculate: What is the efficiency of the energy transfer in this system?
A. 8%
B. 20%
C. 60%
D. 80%
Answer/Explanation
Solution:
Potential energy gain by riding 100 m UP
$\text{mgh}=80 \times 10 \times 100$
$\text{Energy}=8 \times 10^4$
$\text{Power}=\frac{\text{Energy}}{\text{time}}$
$\frac{8 \times 10^4}{500}=\frac{800}{5}=160$
$\begin{aligned} \text { efficiency } & =\frac{\text { useful power out }}{\text { total power in }}\end{aligned}$
$
\begin{aligned}
& \frac{160}{200} \times 100 \% \\
&=80 \%
\end{aligned}
