2021-Nov-Physics_paper_2__TZ0_HL – All Questions with detailed solution
Q.1(a).2021-Nov-Physics_paper_2__TZ2_HL
Topic: Motion
Given: A ball of mass $0.250 \mathrm{~kg}$ is released from rest at time $t=0$, from a height $H$ above a horizontal floor.
The graph shows the variation with time $t$ of the velocity $v$ of the ball. Air resistance is negligible. Take $g=-9.80 \mathrm{~ms}^{-2}$. The ball reaches the floor after $1.0 \mathrm{~s}$.
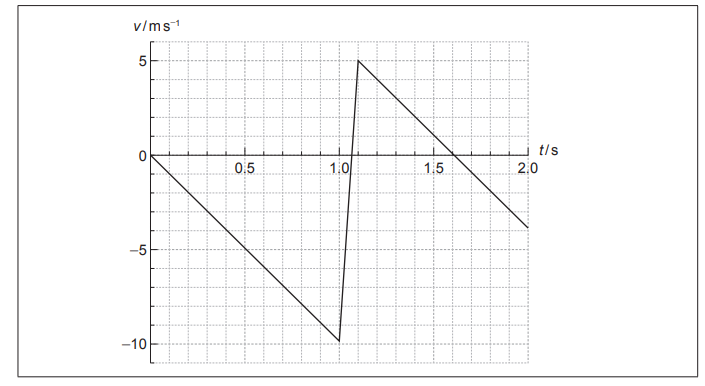
Calculate: $H$.
Answer/Explanation
Solution:
The formula $H=\frac{1}{2}gt^2$ gives the height $H$ from which an object is dropped in terms of the time $t$ it takes to reach the ground, assuming no air resistance.
$$\colorbox{yellow}{$H = \frac{1}{2}gt^2 = \frac{1}{2}(9.80)\cdot(1.0)^2 = 4.90 \mathrm{~m}$}$$
Q.1[(b) (i)].2021-Nov-Physics_paper_2__TZ2_HL
Topic: Motion
Label : the time and velocity graph, using the letter $M$, the point where the ball reaches the maximum rebound height.
Answer/Explanation
Solution:
$\colorbox{yellow}{$\mathrm{M}$ at $1.6 \mathrm{~s}$}$
Q.1[(b) (ii)].2021-Nov-Physics_paper_2__TZ2_HL
Topic: Motion
State: the acceleration of the ball at the maximum rebound height.
Answer/Explanation
Solution:
Q.1[(b) (iii)].2021-Nov-Physics_paper_2__TZ2_HL
Topic: Motion
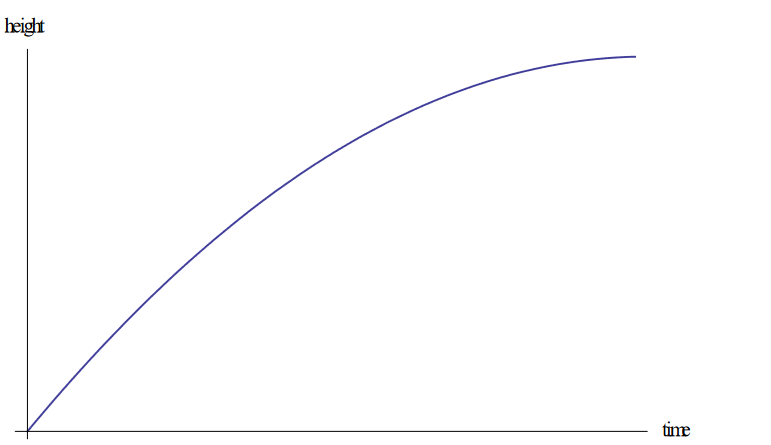
Draw: on the axes, a graph to show the variation with time of the height of the ball from the instant it rebounds from the floor until the instant it reaches the maximum rebound height. No numbers are required on the axes.

Answer/Explanation
Solution:
$H = \frac{1}{2}gt^2$
The graph is a parabolic curve, which is characteristic of objects in free-fall under the influence of gravity.
Q.1(c).2021-Nov-Physics_paper_2__TZ2_HL
Topic: Work, energy and power
Calculate: the loss in the mechanical energy of the ball as a result of the collision with the floor.
Answer/Explanation
Solution:
Using the formula for kinetic energy:
$KE = \frac{1}{2}mv^2$
where:
m = mass of the ball (0.25 kg)
v = final velocity of the ball (5 m/s)
The initial kinetic energy of the ball before it hits the ground is:
$KE_i = \frac{1}{2} \times 0.25 \times 9.8^2 = 12.005\ J$
The final kinetic energy of the ball just before it comes to rest is:
$KE_f = \frac{1}{2} \times 0.25 \times 5^2 = 3.125\ J$
The loss in mechanical energy during the collision is the difference between the initial and final kinetic energies:
Q.1[(d) (i)].2021-Nov-Physics_paper_2__TZ2_HL
Topic: Momentum and impulse
Determine: the average force exerted on the floor by the ball.
Answer/Explanation
Solution:
We can use the impulse-momentum theorem to calculate the average force exerted on the floor by the ball during the collision. The impulse-momentum theorem states that:
$F_{net} \Delta t = \Delta p$
where:
$F_{net}$ = net force exerted on the ball
$\Delta t$ = time interval during which the force is exerted
$\Delta p$ = change in momentum of the ball
We can use the value of velocity from part (c) to find $\Delta p$:
$\Delta p = 0.25 \times (9.8 + 5.0) = 3.7\ kg\ m/s$
The time interval during which the force is exerted is not given, so we will assume it to be 0.1 seconds (which is a reasonable estimate for the duration of a typical collision).
Substituting the values into the impulse-momentum theorem, we get:
$F_{net} \times 0.1 = 3.7$
$F_{net} = \frac{3.7}{0.1} = 37\ N$
This is the net force exerted on the ball by the floor during the collision. However, we are asked to find the average force exerted on the floor by the ball. We can use Newton’s third law of motion (the law of action and reaction) to conclude that the average force exerted on the floor by the ball is equal in magnitude to the net force exerted on the ball by the floor, which is 37 N. Therefore, the average force exerted on the floor by the ball during the collision is approximately 37 N.
Q.2(a).2021-Nov-Physics_paper_2__TZ2_HL
Topic: Travelling waves
A longitudinal wave travels in a medium with speed $340 \mathrm{~ms}^{-1}$. The graph shows the variation with time $t$ of the displacement $x$ of a particle $\mathrm{P}$ in the medium. Positive displacements on the graph correspond to displacements to the right for particle $P$.

Calculate: the wavelength of the wave.
Answer/Explanation
Solution:
Time period(to complete one oscillation) is \mathrm{4~ms} from the graph.
To find the wavelength, we can use the relationship between wavelength, period, and wave speed: $\lambda = vT$.
Given the wave speed $v=340 \mathrm{~ms^{-1}}$ and the period $T=4 \times 10^{-3} \mathrm{s}$, we have:
$$\colorbox{yellow}{$\lambda = vT = (340 \mathrm{~ms^{-1}})(4 \times 10^{-3} \mathrm{s}) = 1.36 \mathrm{~m}$}$$