2023-May-Physics_paper_1__TZ1_SL – All Questions with detailed solution
2023-May-Physics_paper_1__TZ1_SL
Topic: Uncertainties and errors
Discuss: possible wavelength of a visible light photon?
A. \(500 \mu \mathrm{m}\)
B. \(500 \mathrm{~nm}\)
C. \(50 \mu \mathrm{m}\)
D. \(50 \mathrm{~nm}\)
▶️Answer/Explanation
Ans:B
Visible light photons have wavelengths in the range of approximately 400 to 700 nanometers (nm). Different colors of visible light have different wavelengths within this range. So, a wavelength of \(500 \mathrm{~nm}\) falls within the visible light spectrum and is a possible wavelength for a visible light photon.
2023-May-Physics_paper_1__TZ1_SL
Topic: Uncertainties and errors
Given: Masses \(P\) and \(Q\), are measured to be \((30 \pm 1) \mathrm{g}\) and \((20 \pm 1) \mathrm{g}\) respectively.
Calculate:Expressions gives the least percentage uncertainty?
A. \(P+Q\)
B. \(P-Q\)
C. \(P \times Q\)
D. \(\frac{P}{Q}\)
▶️Answer/Explanation
Ans:A
To find the expression that gives the least percentage uncertainty, we need to calculate the percentage uncertainty for each expression and compare them.
1. For \(P + Q\):
The sum of the masses would have an uncertainty of \(1 \mathrm{g} + 1 \mathrm{g} = 2 \mathrm{g}\). The sum is \(30 \mathrm{g} + 20 \mathrm{g} = 50 \mathrm{g}\).
The percentage uncertainty for \(P + Q\) is \(\frac{2 \mathrm{g}}{50 \mathrm{g}} \times 100\% = 4\%.
2. For \(P – Q\):
The difference of the masses would also have an uncertainty of \(1 \mathrm{g} + 1 \mathrm{g} = 2 \mathrm{g}\). The difference is \(30 \mathrm{g} – 20 \mathrm{g} = 10 \mathrm{g}\).
The percentage uncertainty for \(P – Q\) is \(\frac{2 \mathrm{g}}{10 \mathrm{g}} \times 100\% = 20\%.
3. For \(P \times Q\):
The product of the masses would have a percentage uncertainty of \(\sqrt{(\frac{1 \mathrm{g}}{30 \mathrm{g}})^2 + (\frac{1 \mathrm{g}}{20 \mathrm{g}})^2} \times 100\% \approx 7.88\%.
4. For \(\frac{P}{Q}\):
The ratio of the masses would have a percentage uncertainty of \(\sqrt{(\frac{1 \mathrm{g}}{30 \mathrm{g}})^2 + (\frac{1 \mathrm{g}}{20 \mathrm{g}})^2} \times 100\% \approx 7.88\%.
The least percentage uncertainty is in options A and B, which are \(P + Q\) and \(P – Q\) with 4% and 20%, respectively.
Therefore, the answer is A. \(P + Q\) with the least percentage uncertainty.
2023-May-Physics_paper_1__TZ1_SL
Topic: Motion
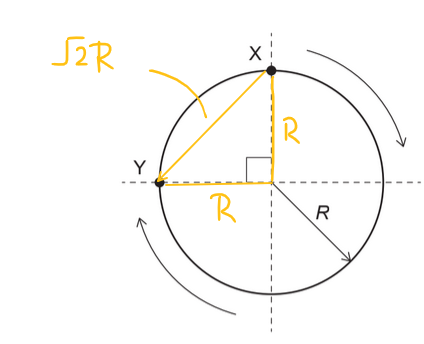
Given: A car travels clockwise around a circular track of radius R.
Calculate: magnitude of displacement from X to Y?
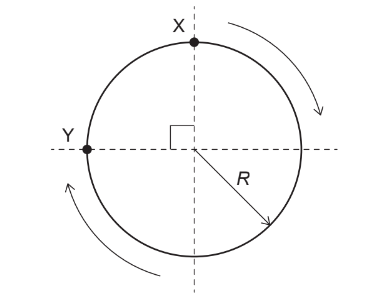
A. \( R \frac{3 \pi}{2}\)
B. \(R \frac{\pi}{2}\)
C. \(R \sqrt{2}\)
D. \(R\)
▶️Answer/Explanation
Ans:C
The displacement from point X to point Y is a chord of the circle and can be represented by the line connecting points X and Y.
2023-May-Physics_paper_1__TZ1_SL
Topic: Motion
Given: A car accelerates uniformly. The car passes point \(X\) at time \(t_1\) with velocity \(v_1\) and point \(Y\) at time \(t_2\) with velocity \(v_2\). The distance \(X Y\) is \(s\).
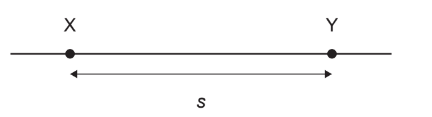
Discuss:expressions are proposed for the magnitude of its acceleration a:
I. \(a=\frac{2 s}{\left(t_2-t_1\right)^2}\)
II. \(a=\frac{v_2^2-v_1^2}{2 s}\)
III. \(a=\frac{v_2-v_1}{t_2-t_1}\)
Which is correct?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Ans:C
To determine which expressions for the magnitude of acceleration (\(a\)) are correct, we can analyze each of the proposed expressions one by one:
I. \(a = \frac{2s}{(t_2 – t_1)^2}\)
Expression I is incorrect because it assumes that the initial velocity \(\left(v_1\right)\) is zero, which may not be the case for the uniformly accelerating car.
II. \(a = \frac{v_2^2 – v_1^2}{2s}\)
This expression is also correct. It’s derived from the kinematic equation for uniformly accelerated motion: \(v^2 = u^2 + 2as\), where \(v_2\) is the final velocity, \(v_1\) is the initial velocity, \(s\) is the displacement, and \(a\) is the acceleration. Solving for \(a\) results in this expression.
III. \(a = \frac{v_2 – v_1}{t_2 – t_1}\)
This expression is also correct and is derived from the definition of acceleration as the rate of change of velocity over time.
So, expressions (II, and III) are correct.
2023-May-Physics_paper_1__TZ1_SL
Topic: Projectile Motion
Given: A ball is projected at an angle to the horizontal on Earth reaching a maximum height H and a maximum range R. The same ball is projected at the same angle and speed on a planet where the acceleration due to gravity is three times that on Earth. Resistance effects are negligible.
Calculate:maximum range and the maximum height reached on that planet?
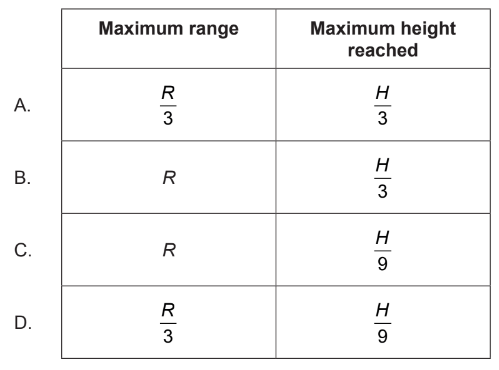
▶️Answer/Explanation
Ans:A
Let’s denote the following variables:
- \(H_e\): The maximum height reached on Earth.
- \(R_e\): The maximum range on Earth.
- \(H_p\): The maximum height reached on the planet with 3 times Earth’s gravity.
- \(R_p\): The maximum range on the planet with 3 times Earth’s gravity.
- \(g_e\): The acceleration due to gravity on Earth.
- \(g_p\): The acceleration due to gravity on the planet.
The maximum range \(R\) for a projectile launched at an angle \(\theta\) with an initial velocity \(V\) on a level surface can be calculated as:
\[R = \frac{V^2 \sin(2\theta)}{g}\]
where \(g\) is the acceleration due to gravity.
On Earth, we have \(g_e\) and \(R_e\), so for the Earth:
\[R_e = \frac{V^2 \sin(2\theta)}{g_e}\]
The maximum height \(H\) can be calculated as:
\[H = \frac{V^2 \sin^2(\theta)}{2g}\]
Now, on the planet with 3 times Earth’s gravity, the acceleration due to gravity is \(g_p = 3g_e\).
We know that the initial velocity and launch angle are the same on both Earth and the planet, so \(V\) and \(\theta\) are constant. We need to calculate \(R_p\) and \(H_p\).
For the planet:
Maximum range on the planet, \(R_p\):
\[R_p = \frac{V^2 \sin(2\theta)}{g_p} = \frac{V^2 \sin(2\theta)}{3g_e} = \frac{1}{3} \left(\frac{V^2 \sin(2\theta)}{g_e}\right) = \frac{1}{3} R_e\]
So, the maximum range on the planet is one-third of the maximum range on Earth.
Maximum height on the planet, \(H_p\):
\[H_p = \frac{V^2 \sin^2(\theta)}{2g_p} = \frac{V^2 \sin^2(\theta)}{2 \cdot 3g_e} = \frac{1}{3} \left(\frac{V^2 \sin^2(\theta)}{2g_e}\right) = \frac{1}{3} H_e\]
The maximum height on the planet is one-sixth of the maximum height on Earth.
So, on the planet with three times the acceleration due to gravity, the maximum range is one-third of the maximum range on Earth, and the maximum height is also one-third of the maximum height on Earth.
