2023-May-Physics_paper_2__TZ1_HL – All Questions with detailed solution
Question
A ball of mass 0.800kg is attached to a string. The distance to the centre of the mass of the ball from the point of support is 95.0cm. The ball is released from rest when the string is horizontal. When the string becomes vertical the ball collides with a block of mass 2.40kg that is at rest on a horizontal surface.
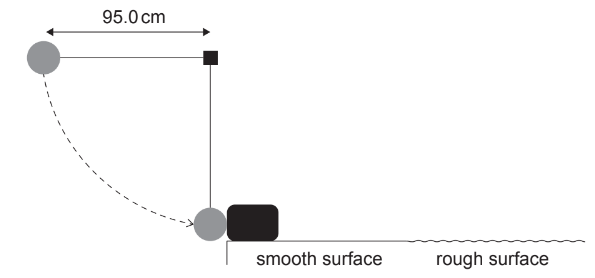
(a) Just before the collision of the ball with the block,
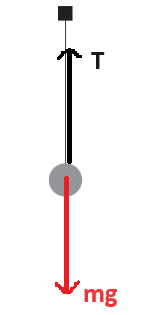
(i) draw a free-body diagram for the ball. [2]
▶️Answer/Explanation
Ans:
(ii) show that the speed of the ball is about \(4.3 \mathrm{~ms}^{-1}\). [1]
▶️Answer/Explanation
Ans:
\[
P E_{\text {initial }}=m g h
\]
where:
\(m=0.800 \mathrm{~kg}\) (mass of the ball)
\(g=9.81 \mathrm{~m} / \mathrm{s}^2\) (acceleration due to gravity)
\(h=0.95 \mathrm{~m}\) (height of the ball from the point of support)
\[
\begin{aligned}
& P E_{\text {initial }}=(0.800 \mathrm{~kg}) \times\left(9.81 \mathrm{~m} / \mathrm{s}^2\right) \times(0.95 \mathrm{~m}) \\
& P E_{\text {initial }}=7.40 \mathrm{~J}
\end{aligned}
\]
At the lowest point, all of the potential energy is converted into kinetic energy.
\[
K E_{\text {final }}=P E_{\text {initial }}
\]
using the kinetic energy to find the speed of the ball:
\[
v=\sqrt{\frac{2 \times K E_{\text {final }}}{m}}
\]
\[
\begin{aligned}
& v=\sqrt{\frac{2 \times 7.40 \mathrm{~J}}{0.800 \mathrm{~kg}}} \\
& v \approx 4.294 \mathrm{~m} / \mathrm{s}
\end{aligned}
\]
(iii) determine the tension in the string. [2]
▶️Answer/Explanation
Ans:
At the lowest point, when the string is vertical and the ball is just about to collide with the block, the forces acting on the ball are its weight (mg) acting downwards and the tension (T) acting upwards. The net force towards the center of the circular path (centripetal force) is provided by the tension in the string.
Using Newton’s second law in the vertical direction:
\[ T – mg = \frac{mv^2}{r} \]
where:
\( T \) is the tension in the string,
\( m \) is the mass of the ball (0.800 kg),
\( g \) is the acceleration due to gravity (9.81 m/s\(^2\)),
\( v \) is the speed of the ball just before the collision (4.3 m/s),
\( r \) is the radius of the circular path (0.95 m).
\[ T – (0.800 \, \text{kg} \times 9.81 \, \text{m/s}^2) = \frac{(0.800 \, \text{kg} \times (4.3 \, \text{m/s})^2)}{0.95 \, \text{m}} \]
\[ T – 7.848 \, \text{N} = \frac{0.800 \times 18.49}{0.95} \, \text{N} \]
\[ T – 7.848 \, \text{N} = 15.44 \, \text{N} \]
\[ T = 15.44 \, \text{N} + 7.848 \, \text{N} \]
\[ T \approx 23.29 \, \text{N} \]
Question
(b) After the collision, the ball rebounds and the block moves with speed 2.16m/s.
(i) Show that the collision is elastic. [4]
▶️Answer/Explanation
Ans:
Given:
Mass of the ball (\(m_{\text{ball}}\)) = 0.800 kg
Initial speed of the ball (\(v_{\text{initial}}\)) = 4.317 m/s
Final speed of the block (\(v_{\text{block}}’\)) = 2.16 m/s
Mass of the block (\(m_{\text{block}}\)) = 2.40 kg
1. Conservation of Momentum:
Before the collision, the total momentum of the system is given by the momentum of the ball:
\[ p_{\text{initial}} = m_{\text{ball}} \times v_{\text{initial}} \]
\[ p_{\text{initial}} = 0.800 \, \text{kg} \times 4.317 \, \text{m/s} \]
\[ p_{\text{initial}} = 3.4536 \, \text{kg·m/s} \]
After the collision, the total momentum of the system is given by the sum of the momenta of the ball and the block:
\[ p_{\text{final}} = m_{\text{ball}} \times v_{\text{ball}}’ + m_{\text{block}} \times v_{\text{block}}’ \]
\[ p_{\text{final}} = 0.800 \, \text{kg} \times v_{\text{ball}}’ + 2.40 \, \text{kg} \times 2.16 \, \text{m/s} \]
\[ p_{\text{final}} = 0.800 \, \text{kg} \times (-2.163) \, \text{m/s} + 5.184 \, \text{kg·m/s} \]
\[ p_{\text{final}} = -1.7304 \, \text{kg·m/s} + 5.184 \, \text{kg·m/s} \]
\[ p_{\text{final}} = 3.4536 \, \text{kg·m/s} \]
The conservation of momentum is satisfied as \( p_{\text{initial}} = p_{\text{final}} \).
2. Conservation of Kinetic Energy:
The initial kinetic energy (\( KE_{\text{initial}} \)) is given by:
\[ KE_{\text{initial}} = \frac{1}{2} \times m_{\text{ball}} \times v_{\text{initial}}^2 \]
\[ KE_{\text{initial}} = \frac{1}{2} \times 0.800 \, \text{kg} \times (4.317 \, \text{m/s})^2 \]
\[ KE_{\text{initial}} = \frac{1}{2} \times 0.800 \, \text{kg} \times 18.6039 \, \text{m}^2/\text{s}^2 \]
\[ KE_{\text{initial}} = 7.44156 \, \text{J} \]
The final kinetic energy (\( KE_{\text{final}} \)) is given by the sum of the kinetic energies of the ball and the block:
\[ KE_{\text{final}} = \frac{1}{2} \times m_{\text{ball}} \times v_{\text{ball}}’^2 + \frac{1}{2} \times m_{\text{block}} \times v_{\text{block}}’^2 \]
\[ KE_{\text{final}} = \frac{1}{2} \times 0.800 \, \text{kg} \times (2.163 \, \text{m/s})^2 + \frac{1}{2} \times 2.40 \, \text{kg} \times (2.16 \, \text{m/s})^2 \]
\[ KE_{\text{final}} = \frac{1}{2} \times 0.800 \, \text{kg} \times 4.677 \, \text{m}^2/\text{s}^2 + \frac{1}{2} \times 2.40 \, \text{kg} \times 4.6656 \, \text{m}^2/\text{s}^2 \]
\[ KE_{\text{final}} = 7.4406 \, \text{J} \]
The conservation of kinetic energy is satisfied as \( KE_{\text{initial}} = KE_{\text{final}} \).
Since both momentum and kinetic energy are conserved, we can conclude that the collision is elastic.
(ii) Calculate the maximum height risen by the centre of the ball. [2]
▶️Answer/Explanation
Ans:
To calculate the maximum height risen by the center of the ball after the collision, we can use the principle of conservation of mechanical energy.
At the maximum height, all of the kinetic energy of the ball has been converted into gravitational potential energy.
Given:
Mass of the ball (\(m_{\text{ball}}\)) = 0.800 kg
Final speed of the ball (\(v_{\text{ball}}’\)) = 2.16 m/s
Acceleration due to gravity (\(g\)) = 9.8 m/s\(^2\)
Using the conservation of mechanical energy:
\[ \text{Kinetic energy at the lowest point} = \text{Potential energy at the maximum height} \]
\[ \frac{1}{2} \times m_{\text{ball}} \times v_{\text{ball}}’^2 = m_{\text{ball}} \times g \times h \]
\[ \frac{1}{2} \times 0.800 \times (2.16)^2 = 0.800 \times 9.8 \times h \]
\[ h = \frac{\frac{1}{2} \times 0.800 \times (2.16)^2}{0.800 \times 9.8} \]
\[ h = \frac{0.5 \times 0.800 \times 4.6656}{0.800 \times 9.8} \]
\[ h = \frac{1.86528}{9.8} \]
\[ h \approx 0.238 \, \text{m} \]
So, the maximum height risen by the center of the ball after the collision is approximately \(0.238 \, \text{m}\).
(c) The coefficient of dynamic friction between the block and the rough surface is 0.400.
Estimate the distance travelled by the block on the rough surface until it stops. [3]
▶️Answer/Explanation
Ans:
To estimate the distance traveled by the block on the rough surface until it stops, we can use the work-energy principle. The work done by the friction force (opposing the motion) will decrease the kinetic energy of the block until it comes to a stop.
Given:
Coefficient of dynamic friction (\(\mu\)) = 0.400
Mass of the block (\(m_{\text{block}}\)) = 2.40 kg
Initial speed of the block (\(v_{\text{block}}’\)) = 2.16 m/s
Acceleration due to gravity (\(g\)) = 9.8 m/s\(^2\)
The work done by the friction force is given by:
\[ W_{\text{friction}} = \mu \cdot m_{\text{block}} \cdot g \cdot d \]
where:
\( W_{\text{friction}} \) is the work done by the friction force,
\( d \) is the distance traveled by the block.
The work done by the friction force decreases the kinetic energy of the block, given by:
\[ KE = \frac{1}{2} \cdot m_{\text{block}} \cdot v_{\text{block}}’^2 \]
At the point where the block stops, all of its kinetic energy has been converted into work done by the friction force. Therefore, we can equate the work done by the friction force to the initial kinetic energy of the block.
\[ \mu \cdot m_{\text{block}} \cdot g \cdot d = \frac{1}{2} \cdot m_{\text{block}} \cdot v_{\text{block}}’^2 \]
\[ \mu \cdot g \cdot d = \frac{1}{2} \cdot v_{\text{block}}’^2 \]
\[ d = \frac{\frac{1}{2} \cdot v_{\text{block}}’^2}{\mu \cdot g} \]
Plugging in the given values:
\[ d = \frac{\frac{1}{2} \cdot (2.16)^2}{0.400 \cdot 9.8} \]
\[ d = \frac{\frac{1}{2} \cdot 4.6656}{3.92} \]
\[ d \approx \frac{2.3328}{3.92} \]
\[ d \approx 0.596 \, \text{m} \]
So, the estimated distance traveled by the block on the rough surface until it stops is approximately \(0.596 \, \text{m}\).
Question
A solid piece of chocolate of mass \(82 \mathrm{~g}\) is placed in a pan over fire. Thermal energy is transferred to the chocolate at a constant rate. The graph shows the variation with time \(t\), of the temperature \(T\) of the chocolate. At 6.0 minutes all the chocolate has melted.
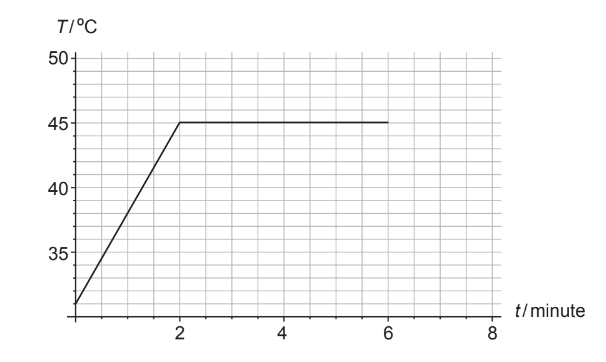
The specific heat capacity of solid chocolate is \(1.6 \times 10^3 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\).
(a) Show that the average rate at which thermal energy is transferred into the chocolate is about \(15 \mathrm{~W}\).[3]
▶️Answer/Explanation
Ans:
Given:
Mass of the chocolate (\(m\)) = \(82 \, \text{g} = 0.082 \, \text{kg}\)
Specific heat capacity of solid chocolate (\(c\)) = \(1.6 \times 10^3 \, \text{J/kg/K}\)
Change in temperature \(\Delta T=45^{\circ} \mathrm{C}-31^{\circ} \mathrm{C}=14^{\circ} \mathrm{C}\)
Time taken for the chocolate to melt (\(t_{\text{melt}}\)) = \(2.0 \, \text{minutes} = 120 \, \text{seconds}\)
The thermal energy transferred into the chocolate is given by:
\[ Q = mc \Delta T \]
\[ Q = (0.082 \, \text{kg}) \times (1.6 \times 10^3 \, \text{J/kg/K}) \times (14 \, \text{K}) \]
\[ Q = 1.84 \times 10^3 \, \text{J} \]
The average rate at which thermal energy is transferred into the chocolate (\( P_{\text{avg}} \)) is given by:
\[ P_{\text{avg}} = \frac{Q}{t_{\text{melt}}} \]
\[ P_{\text{avg}} = \frac{1.84 \times 10^3 \, \text{J}}{120 \, \text{s}} \]
\[ P_{\text{avg}} \approx 15.3 \, \text{W} \]
Rounded to one decimal place, the average rate at which thermal energy is transferred into the chocolate is approximately \(15 \, \text{W}\).
