2023-May-Physics_paper_2__TZ2_SL – All Questions with detailed solution
Question
A toy rocket is made from a plastic bottle that contains some water. Air is pumped into the vertical bottle until the pressure inside forces water and air out of the bottle. The bottle then travels vertically upwards.
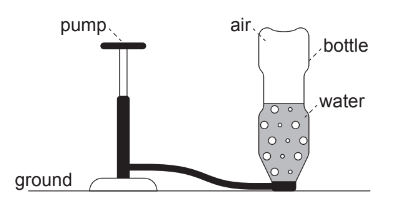
The air–water mixture is called the propellant. The variation with time of the vertical velocity of the bottle is shown.
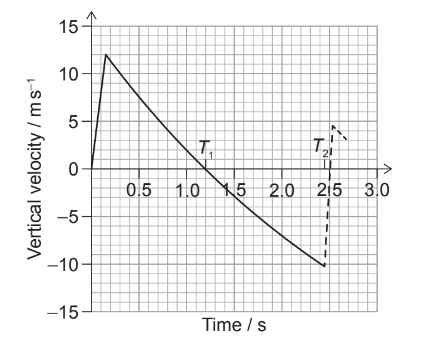
The bottle reaches its highest point at time \(T_1\) on the graph and returns to the ground at time \(T_2\). The bottle then bounces. The motion of the bottle after the bounce is shown as a dashed line.
(a) Estimate, using the graph, the maximum height of the bottle.[3]
▶️Answer/Explanation
Ans:
Area under v-t graph will give maximum height .
\( \begin{gathered}\frac{1}{2} \times 12 \mathrm{~m/s} \times 1.2~ \mathrm{sec} \\ =7.2 \mathrm{~m}\end{gathered} \)
Question
(b) Estimate the acceleration of the bottle when it is at its maximum height. [2]
▶️Answer/Explanation
Ans:
acceleration will be here g which is equal to 9.8 m/s2
Question
(c) The bottle bounces when it returns to the ground.
(i) Calculate the fraction of the kinetic energy of the bottle that remains after the bounce.
▶️Answer/Explanation
Ans:
(KE) ratio using the formula:
\[
\left(\frac{v_{\text {final }}}{v_{\text {Initial }}}\right)^2
\]
Given that \(v_{\text {initial }}=10 \mathrm{~m} / \mathrm{s}\) and \(v_{\text {final }}=4.5 \mathrm{~m} / \mathrm{s}\),
\[
\left(\frac{4.5}{10}\right)^2=\left(\frac{9}{20}\right)^2
\]
Now, let’s simplify this expression:
\[
\left(\frac{9}{20}\right)^2=\frac{81}{400}
\]
This can also be expressed as a decimal:
\[
\frac{81}{400}=0.2025
\]
Or as a percentage:
\[
0.2025 \times 100 \%=20.25 \%
\]
Therefore, the kinetic energy ratio is approximately \(20.25 \%\) or \(\frac{81}{400}\) or \(\frac{1}{5}\). Each of these expressions represents the ratio of the final kinetic energy to the initial kinetic energy.
Question
(ii) The mass of the bottle is 27g and it is in contact with the ground for 85ms. Determine the average force exerted by the ground on the bottle. Give your answer to an appropriate number of significant figures. [3]
▶️Answer/Explanation
Ans:
To determine the average force exerted by the ground on the bottle, we can use Newton’s second law of motion, which states:
\[ F = \frac{\Delta p}{\Delta t} \]
First, let’s calculate the change in momentum \( \Delta p \):
\[ \Delta p = p_{\text{final}} – p_{\text{initial}} \]
Given that the mass of the bottle is \( 27 \, \text{g} \), we need to convert it to kilograms:
\[ \text{Mass} = 27 \, \text{g} = 0.027 \, \text{kg} \]
Now, we can calculate the initial momentum \( p_{\text{initial}} \) and the final momentum \( p_{\text{final}} \):
\[ p_{\text{initial}} = m \times v_{\text{initial}} = 0.027 \, \text{kg} \times (-10 \, \text{m/s}) \]
\[ p_{\text{final}} = m \times v_{\text{final}} = 0.027 \, \text{kg} \times (4.5 \, \text{m/s}) \]
Next, let’s calculate the change in time \( \Delta t \):
\[ \Delta t = 85 \, \text{ms} = 0.085 \, \text{s} \]
Now, we can substitute these values into the formula for average force:
\[ F = \frac{p_{\text{final}} – p_{\text{initial}}}{\Delta t} \]
\[ F = \frac{0.027 \times 4.5 – 0.027 \times (-10)}{0.085} \]
\[ F = \frac{0.1215 + 0.270}{0.085} \]
\[ F = \frac{0.3915}{0.085} \]
\[ F \approx 4.61 \, \text{N} \]
Therefore, the average force exerted by the ground on the bottle is approximately \( 4.61 \, \text{N} \).
Question
(d) After a second bounce, the bottle rotates about its centre of mass. The bottle rotates at 0.35 revolutions per second.
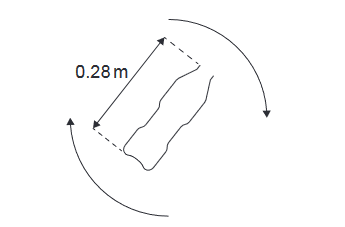
The centre of mass of the bottle is halfway between the base and the top of the bottle. Assume that the velocity of the centre of mass is zero.
Calculate the linear speed of the top of the bottle.
▶️Answer/Explanation
Ans:
To calculate the linear speed of the top of the bottle, we can use the relationship between linear speed and angular speed:
\[
v = r \cdot \omega
\]
Given that the bottle rotates at \( 0.35 \) revolutions per second, we first need to convert this angular speed to radians per second since \( 1 \) revolution is equal to \( 2\pi \) radians. Thus:
\[
\omega = 0.35 \text{ revolutions per second} \times 2\pi \text{ radians per revolution}
\]
\[
\omega = 0.35 \times 2\pi \text{ rad/s}
\]
\[
\omega = 0.35 \times 2\pi \text{ rad/s} \approx 2.199 \text{ rad/s}
\]
Now, we can calculate the linear speed of the top of the bottle using the given radius \( r = 0.14 \) m:
\[
v = 0.14 \text{ m} \times 2.199 \text{ rad/s}
\]
\[
v \approx 0.14 \times 2.199 \text{ m/s}
\]
\[
v \approx 0.30786 \text{ m/s}
\]
So, the linear speed of the top of the bottle is approximately \( 0.30786 \) m/s.
Question
(e) The maximum height reached by the bottle is greater with an air–water mixture than with only high-pressure air in the bottle.
Assume that the speed at which the propellant leaves the bottle is the same in both cases Explain why the bottle reaches a greater maximum height with an air–water mixture. [2]
▶️Answer/Explanation
Ans:
The bottle reaches a greater maximum height with an air-water mixture compared to only high-pressure air in the bottle due to the difference in the impulse experienced by the bottle in each scenario.
Impulse is defined as the change in momentum of an object, and it is equal to the force applied to the object multiplied by the time over which the force is applied. In this case, the force is exerted by the expanding gas (propellant) as it pushes against the inside of the bottle, and the time over which this force is applied is the duration of the propellant’s expulsion from the bottle.
Given that the speed at which the propellant leaves the bottle is the same in both cases, the impulse experienced by the bottle is the same. However, the mass of the air-water mixture is greater than the mass of only high-pressure air in the bottle, due to the added mass of the water.
According to the impulse-momentum theorem, which states that the impulse experienced by an object is equal to the change in momentum of the object, the change in momentum of the bottle will be greater when it is filled with the air-water mixture compared to only high-pressure air. This greater change in momentum results in a greater upward force exerted on the bottle during its expulsion, leading to a higher launch velocity and consequently a greater maximum height reached by the bottle when filled with an air-water mixture.
