SAT Math: Practice Questions-Additional topics in math-Volume word problems

SAT MathsSAT EnglishSAT Practice Tests -(Full -Length)

SAT Math Practice Questions-All Topics

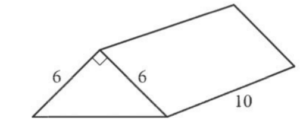
Question

What is the volume, in cubic units, of the right triangular prism shown?

  1. 22
  2. 60
  3. 180
  4. 360
Answer/Explanation

Ans: C

Question

The mass of a piece of wood is 10.0 grams. The volume of the wood is 12.5 cubic centimeters. What is the density, in grams per cubic centimeter, of the piece of wood? (Density equals mass divided by volume.)

  1. 0.80
  2. 1.25
  3. 2.50
  4. 22.5
Answer/Explanation

Ans: A

Question

The volume of a neodymium magnet is 2.50 cubic centimeters, and its mass is 18.5 grams. What is the density, in grams per cubic centimeter, of the magnet?

  1. 0.140
  2. 7.40
  3. 16.0
  4. 46.3
Answer/Explanation

Ans: B

Question

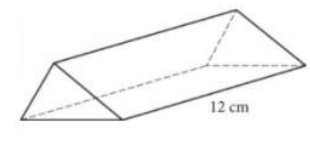
The volume of the right triangular prism shown is 96 cubic centimeters (cm3). What is the area, in cm2, of one of the triangular bases of the prism?

  1. 4
  2. 8
  3. 16
  4. 42
Answer/Explanation

Ans: B

Question

For a certain type of aircraft, the ratio of thrust, in newtons, to weight, in newtons, is 27 to 100. If an aircraft has a weight of3,730,000 newtons, which of the following is closest to the thrust, in newtons, of the aircraft? 

  1. 1,010,000
  2. 13,800,000
  3. 101,000,000
  4. 373,000,000
Answer/Explanation

Ans: A

Question

A liquid mixture is composed of four components, and the table shows the percentage, by volume, of each component. The volume of each component prior to mixing is the same as the volume of that component in the mixture. A procedure can be used to extract the individual components that were combined to form the liquid mixture. When the procedure is applied to extract the components in the mixture, a portion of the volume of the components may be lost.

The procedure was applied to a new sample of 9.00 milliliters of the liquid mixture to extract component C. Due to the loss of volume from the procedure, the extracted volume of component C was only 90.0% of the original volume of this component. What was the extracted volume of component C, in milliliters? 

Answer/Explanation

Ans: 1.62

More SAT Math Practice Questions.............
Scroll to Top