SAT Math: Practice Questions-Problem solving and data analysis-Percents

SAT MathsSAT EnglishSAT Practice Tests -(Full -Length)

SAT Math Practice Questions-All Topics

Question

In 480 BC, the population of the Persian Empire was approximately 49.4 million. The population of the Persian Empire was 44% of the world population at that time. Which of the following is the best estimate of the world population in 480 BC? 

  1. 21.7 million
  2. 89.1 million
  3. 93.4 million
  4. 112.3 million
Answer/Explanation

Ans: D

Question

A quantity is decreased by 45 % of its value. The resulting value is \(x\). Which expression gives the value of the original quantity in terms of \(x\)?

  1. \(\frac{x}{0.45}\)
  2. \(\frac{x}{0.55}\)
  3. \(\frac{x}{1.45}\)
  4. \(\frac{x}{1.55}\)
Answer/Explanation

Ans: B

Question

There are a total of 1000 four-digit numbers from 1000 to 1999. If one of these numbers is selected at random, what is the probability that the number is greater than 1499?

Answer/Explanation

Ans: .5, 1/2

Question

The table gives the age groups of the total population of women and the number of registered women voters in the United States in 2012, rounded to the nearest million.

Total population of women (in millions) Registered women voters(in millions)

18 to 24 years old                       15                                                                 8

25 to 44 years old                       41                                                               25

45 to 64 years old                       42                                                               30

65 to 74 years old                        13                                                               10

75 years old and over                 11                                                                8

Total                                                    122                                                               81

In 2012, the number of registered women voters was \(p\)% of the total population of women. What is the value of \(p\), to the nearest whole number?

Answer/Explanation

Ans: 66

Question

If a woman is selected at random from the total population of women ages 45 to 64 years old, what is the probability of selecting a registered woman voter, rounded to the nearest hundredth? (Express your answer as a decimal, not as a percent.)

Answer/Explanation

Ans: .71, 71/100

Question

The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?

  1. 0.4
  2. 0.5
  3. 0.6
  4. 1
Answer/Explanation

Ans: C

Question

A local restaurant gives teachers a 20% discount on all their meals. If a teacher pays \($\)14.00 for a meal after the discount was applied, what was the price of the meal before the discount?

  1. \($\)16.80
  2. \($\)17.50
  3. \($\)20.00
  4. \($\)25.20
Answer/Explanation

Ans: B

Question

An advertising agency guarantees that its services will increase website traffic by 3.5% compared to each previous week. Which type of function best models the weekly guaranteed website traffic as the number of weeks increases?

  1. Increasing exponential
  2. Decreasing exponential
  3. Increasing linear
  4. Decreasing linear
Answer/Explanation

Ans: A

Question

Each year the value of an investment increases by 2.5% of the previous year’s value. The initial value of the investment was $500. Which equation gives the value of the investment \(y\), in dollars, \(x\) years after the initial investment was made?

A) \(y\) = 500(0.25)\(x\)
B) \(y\) = 500(1.025)\(x\)
C) \(y\) = 500(1.25)\(x\)
D) \(y\) = 500(2.5)\(x\)

Answer/Explanation

Ans: B

Question

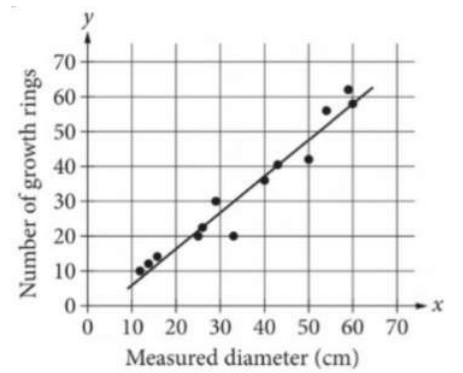
For a sample of 13 red alder trees, an arborist measured each tree’s diameter, in centimeters (cm), at a height of 1.4 meters. The arborist then counted the number of growth rings at this height. Each point in the scatterplot represents the diameter and number of rings for each tree. A line of best fit for these data is also shown.

A red alder tree will be selected at random from the sample. What is the probability that the selected tree will have a measured diameter that is greater than 30 cm?

  1. 1/7
  2. 6/13
  3. 7/13
  4. 6/7
Answer/Explanation

Ans: C

Question

For how many of the trees in the sample is the number of growth rings greater than the number predicted by the line of best fit?

  1. 3
  2. 4
  3. 6
  4. 10
Answer/Explanation

Ans: C

More SAT Math Practice Questions.............
Scroll to Top