Question
The ratio of students to teachers in a high school is 18 to 1. If the school has 105 teachers, how many students does it have?
Answer/Explanation
Ans: 1890
Question
Two beach balls are each in the shape of a sphere. The larger beach ball has a diameter of 3\(x\), and the smaller beach ball has a diameter of \(x\). What is the ratio of the volume of the larger beach ball to the volume of the smaller beach ball?
- 3 to 1
- 6 to 1
- 9 to 1
- 27 to 1
Answer/Explanation
Ans: D
Question
In 2015, the city of Miami had a population of 441,000 people and an area of 36 square miles. What was the population density of Miami, in people per square mile, in 2015?
- 10,750
- 12,250
- 14,250
- 16,750
Answer/Explanation
Ans: B
Question
The combustion of glucose releases energy. The ratio of grams of glucose combusted to kilocalories of energy released is 12.0 to 45.0. How many grams of glucose must be combusted to provide 85.5 kilocalories of energy?
- 5.7
- 9.9
- 22.8
- 320.6
Answer/Explanation
Ans: C
Question
What percentage of 40 is 15?
- 62.5%
- 37.5%
- 32.5%
- 2.70%
Answer/Explanation
Ans: B
Question
Object A has a mass of \(x\) kilograms (kg). Object B has a mass of 1.1\(x\) kg. What is the ratio of the mass of object A to the mass of object B?
- 1 to 1
- 1 to 11
- 10 to 1
- 10 to 11
Answer/Explanation
Ans: D
Question
As of 2016, there were 118 known elements. These elements can be described with 10 classifications as summarized in the given table.
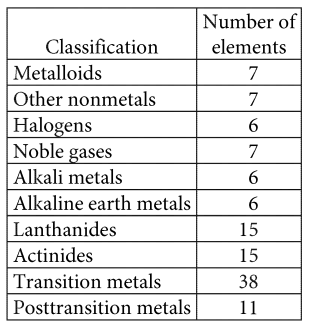
An element is a nonmetal if it is classified as a halogen, noble gas, or other nonmetal. The ratio of all nonmetals to all elements is 10 to \(k\). What is the value of \(k\)?
Answer/Explanation
Ans: 59
