Question 1
Given
- Three cities Lucknow (L), Jaipur (J) and Delhi (D), are represented on below triangle.
- Lucknow lies 500km directly east of Jaipur, and \(\hat{JLD}\) = 25°
- The bearing of D from J is 34°.
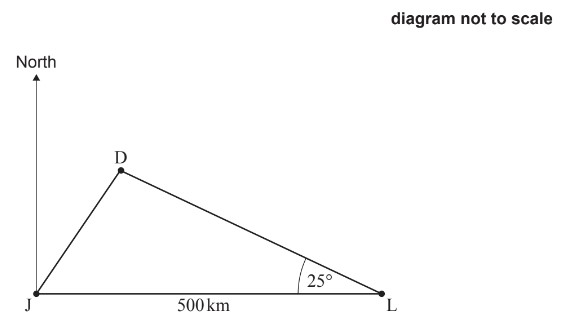
Find
- Find \(\hat{JDL}\)
- distance between Lucknow and Delhi
▶️Answer/Explanation
Answer:
(a) Let N be North
\(\hat{NJD} = 34^0 \) OR \(\hat{DJL} = 56^0\) (must be labelled or indicated in diagram):
\(\hat{JDL} = 99(^0)\)
Let N be North
Given the bearing of D from J \(\hat{NJD} = 34^0 \)
\(\hat{DJL}=\hat{NJL}-\hat{NJD} \Rightarrow 90^0-34^0=56^0\)
To find \(\hat{JDL}\),we can use the fact that the sum of angles in any triangle is \(180^0\). Therefore:
\(\hat{JDL}=180^0-\hat{NJD}-\hat{DJL} \Rightarrow 180^0-34^0-56^0=90^0\)
\(\hat{JDL}=90^0\)
(b) attempt to apply the sine rule
\(\frac{DL}{sin 56^0} = \frac{500}{sin 99^0}\) OR \(\frac{DL}{sin 0.977384…} = \frac{500}{sin 1.72787…}\)
419.685
DL = 420 (km)
\(\hat{DJL} = 56^0 \) —-part (a)
The distance between Jaipur and Lucknow (JL) is 500 km.
Using the sine rule:
\(\frac{DL}{sin\hat{DJL}}=\frac{JL}{sin\hat{JDL}}\)
Substitute the given values:
\(\frac{DL}{sin 56^0 }=\frac{500}{sin 90^0}\)
Now, calculate:
\(DL=500\times \frac{sin 56^0}{sin 90^0}\)
DL≈419.685
So, the distance DL between Lucknow and Delhi is approximately 419.685 km, which rounds to 420 km.
Question 2
Given
- The car value is given by the function C = \(40 000(0.91)^t\), where t is in years since January 1, 2023, and C is in USD.
Find
- Find the annual rate of depreciation for the car
- Car value as of January 1, 2028
- Aayush wants to buy this car. On January 1, 2023, he invested $15, 000 in an account that earns 3% annual interest compounded annually. He makes no further deposits to or withdrawals from the account. Aayush wishes to buy this car for its value on January 1, 2028. In addition to the money in his account, he will need an extra $M. Find Value of M
▶️Answer/Explanation
Answer:
(a) 9% (accept 0.09)
The annual rate of depreciation can be determined by examining the decay factor in the exponential function. In the given function,
The formula for the decay factor is \(A = P(1-r)^{t}\)
where
- is the final amount.
- P is the initial amount.
- r is the decay factor.
- is the time in years.
Comparing this to the given function,\(r=1-0.91\Rightarrow 0.09\)
The annual rate of depreciation is 0.09, or 9%. Therefore, the car depreciates by 9 each year.
(b) t = 5 (seen anywhere)
24961.28…
25000 (dollars)
To find the car value as of January 1, 2028, you can substitute t= into the given function C = \(40 000(0.91)^t\)
C = \(40 000(0.91)^5\)
Now, calculate:
Therefore, the car value as of January 1, 2028, is approximately $24,961.28 (≈$25000).
(c) EITHER
n = 5
1% = 3
PV 15000 = (\(\pm \)) 15000
P/Y = 1
C/Y = 1
(\(\Rightarrow \) = (\(\pm \)) FV 17389.11…)
OR
15 000\((1 + \frac{3}{100})^5 \) (=17389.11…)
THEN
subtracting their value from their answer to part (b)
7572.17 …
7570 (dollars)
To find the extra amount (M) that Aayush needs in addition to the money in his account to buy the car, we can use the compound interest formula.
The formula for compound interest is given by: \(A=P\left (1+\frac{r}{n} \right )^{nt}\)
where:
- A is the amount after years.
- P is the principal amount (initial investment).
- r is the annual interest rate (in decimal form),
- n is the number of times interest is compounded per year, and
In this case,
- P = $15,000,
- n = 1 (compounded yearly), and
Let’s calculate the future value of Aayush’s investment after 5 years:
\(A=15000\left (1+\frac{0.03}{1} \right )^{1\times 5}\)
\(A=15000\left (1+0.03 \right )^{5}\)
Now, to find the extra amount,
, subtract the future value of the investment from the car value:
Therefore, Aayush needs an extra amount of approximately $7,572.17 to buy the car on January 1, 2028.