Question
The following diagram shows two buildings situated on level ground.
From point P on the ground directly between the two buildings, the angle of elevation to the top of each building is θ.
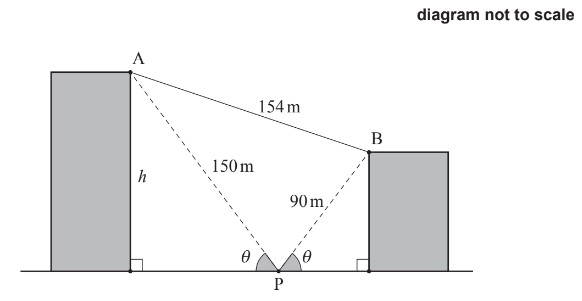
The distance from point P to point A at the top of the taller building is 150 metres.
The distance from point P to point B at the top of the shorter building is 90 metres.
The distance between A and B is 154 metres.
(a) Find the measure of \(\hat{APB}\).
(b) Find the height, h, of the taller building.
▶️Answer/Explanation
Answer:
(a) attempt to substitute into cosine rule
\(154^2 = 150^2 + 90^2 – 2(150)(90)cos \hat{APB}\) OR \(cos \hat{APB}=\frac{150^2+90^2-154^2}{2(150)(90)}\)
\(\hat{APB} = 75.2286…^0\) OR 1.31298… radians
\(\hat{APB}=75.2^0\) OR 1.31 radians
(b) valid approach to find θ
\(θ= \frac{180^0 – \hat{APB}}{2}\) OR \(θ=\frac{180^0-75.2286…^0}{2}\) (=52.3856…) OR
\(θ=\frac{\pi – 1.31298…}{2}\) (=0.914302…)
valid approach to express h in terms of θ
\(sin θ = \frac{h}{150}\) OR h = 150sin52.3856…\(^0\)
h = 118.820…
h = 119 (m)
Question 7. [Maximum mark: 13]
The six blades of a windmill rotate around a centre point C. Points A and B and the base of
the windmill are on level ground, as shown in the following diagram
From point A the angle of elevation of point C is 0.6 radians.
(a) Given that point A is 12 metres from the base of the windmill, find the height of point C above the ground. [2]
An observer walks 7 metres from point A to point B.
(b) Find the angle of elevation of point C from point B. [2]
The observer keeps walking until he is standing directly under point C. The observer has a height of 1.8 metres, and as the blades of the windmill rotate, the end of each blade passes 2.5 metres over his head.
(c) Find the length of each blade of the windmill. [2]
One of the blades is painted a different colour than the others. The end of this blade is labelled point D. The height h , in metres, of point D above the ground can be modelled by the function \(h\left ( t \right )=p\cos \left ( \frac{3\pi }{10}t \right )=q\) , where t is in seconds and \(p,q\epsilon R\) When t = 0, point D is at its maximum height.
(d) Find the value of p and the value of q. [4]
If the observer stands directly under point C for one minute, point D will pass over his
head n times.
(e) Find the value of n .
Answer/Explanation
(a) \(\tan 0.6=\frac{h}{12}\)
8.20964…
8.21(m)
(b)
\(\tan B=\frac{8.2096..}{5}\) OR \(\tan ^{-1}1.6419\)
1.02375
1.02(radians) ( accept \(58.7^{\circ}\)
(c)\( x+1.8+2.5=8.20964….\) ( or equivalent )
3.90964..
3.91(m)
(d) METHOD 1
recognition that blade length =amplitude , \(p=\frac{max-min}{2}\) p=3.91
centre of windmill =vertical shift ,\(q=\frac{max+min}{2}\)
q=8.21
METHOD 2
attempting to form two equations in terms of p and q
\(12.1192…=p\cos \left ( \frac{3\pi }{10} .0\right )+q\), \(4.3000…=p\cos \left ( \frac{3\pi }{10} .\frac{10}{3}\right )+q\)
(e) appropriate working towards finding the period
period =\(\frac{2\pi }{\frac{3\pi }{10}}\) (=6.6666…)
rotations per minute =\(\frac{60}{their period }\)
n=9(must be an integer )(accept n=10,n=18,n=19)
