Question
What is the enthalpy change of the reaction, in kJ?
2C (graphite) +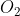 
(g) → 2CO (g)
Substance | ∆ |
C (graphite) | –394 |
CO (g) | –283 |
A –394 – 283
B 2 (–394) + 2 (–283)
C –394 + 283
D 2 (–394) + 2 (283)
▶️Answer/Explanation
Ans: D
C(graphite) + O2(g) → CO2(g) ΔH1 = -394 kJ/mol …(Eqn 1)
CO(g) + 1/2O2(g) → CO2(g) ΔH2 = -283 kJ/mol ….(Eqn 2)
Multiplying Eqn 1 and Eqn 2 with 2, and then subtracting Eqn 2 from it, we get,
2C (graphite) + 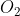(g) → 2CO (g) ….. (Eqn 3)
(Eqn)3 = 2(Eqn1) – 2(Eqn2)
ΔH3 = 2(ΔH1)-2(ΔH2)
ΔH3 = 2 (–394) + 2 (283)
Question
Consider the equations below.
\[\begin{array}{*{20}{l}} {{\text{C}}{{\text{H}}_{\text{4}}}{\text{(g)}} + {{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{HCHO(l)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}}}&{\Delta {H^\Theta } = x} \\ {{\text{HCHO(l)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {\text{HCOOH(l)}}}&{\Delta {H^\Theta } = y} \\ {2{\text{HCOOH(l)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {{{\text{(COOH)}}}_2}({\text{s)}} + {{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = z} \end{array}\]
What is the enthalpy change of the reaction below?
\[2{\text{C}}{{\text{H}}_4}{\text{(g)}} + {\text{3}}\frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {{\text{(COOH)}}_2}{\text{(s)}} + 3{{\text{H}}_2}{\text{O(l)}}\]
A. \(x + y + z\)
B. \(2x + y + z\)
C. \(2x + 2y + z\)
D. \(2x + 2y + 2z\)
▶️Answer/Explanation
C
The enthalpy change of a reaction that is the sum of two or three reactions with known enthalpy changes. In this question three reactions were given with corresponding enthalpy change values of x, y and z. Hence, by multiplying given equations 1 and 2 with 2 and adding them to the third equation, we obtain the reaction for which enthalpy change is to be calculated. Hence, the final enthalpy change of the required reaction could be determined as \(C = 2x + 2y + z\).
Question
Given the enthalpy change for the reaction below:
\[\begin{array}{*{20}{l}} {{\text{2}}{{\text{H}}_{\text{2}}}{\text{(g)}} + {{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{2}}{{\text{H}}_{\text{2}}}{\text{O(l)}}}&{\Delta {H^\Theta } = – 572{\text{ kJ}}} \end{array}\]
which statement is correct?
A. The standard enthalpy change of combustion of \({{\text{H}}_2}{\text{(g)}}\) is \( – 286{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
B. The standard enthalpy change of combustion of \({{\text{H}}_2}{\text{(g)}}\) is \( + 286{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
C. The standard enthalpy change of formation of \({{\text{H}}_2}{\text{O(l)}}\) is \( – 572{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
D. The standard enthalpy change of formation of \({{\text{H}}_2}{\text{O(l)}}\) is \( + 572{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
▶️Answer/Explanation
A
Standard enthalpy of combustion is defined as the enthalpy change when one mole of a compound is completely burnt in oxygen with all the reactants and products in their standard state under standard conditions (298K and 1 bar pressure).
Here, 2 moles of H2 undergo combustion and enthalpy change is given as -572.
So, for combustion of 1 mole of H2, the standard enthalpy change of combustion of \({{\text{H}}_2}{\text{(g)}}\) would be \( – 286{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
Question
Consider the two reactions involving iron and oxygen.
\[\begin{array}{*{20}{l}} {{\text{2Fe(s)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2FeO(s)}}}&{\Delta {H^\Theta } = – 544{\text{ kJ}}} \\ {{\text{4Fe(s)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{2F}}{{\text{e}}_2}{{\text{O}}_3}{\text{(s)}}}&{\Delta {H^\Theta } = – 1648{\text{ kJ}}} \end{array}\]
What is the enthalpy change, in kJ, for the reaction below?
\[{\text{4FeO(s)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2F}}{{\text{e}}_2}{{\text{O}}_3}{\text{(s)}}\]
A. \( – 1648 – 2( – 544)\)
B. \( – 544 – ( – 1648)\)
C. \( – 1648 – 544\)
D. \( – 1648 – 2(544)\)
▶️Answer/Explanation
A
The required equation can be obtained by multiplying the first equation with 2 and then subtracting it from the second equation.
Required equation = (Second Equation) -2(First equation)
Hence, enthalpy change of Required equation = -1648 – 2(-544)
Question
Enthalpy changes of reaction are provided for the following reactions.
\[\begin{array}{*{20}{l}} {{\text{2C(s)}} + {\text{2}}{{\text{H}}_2}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_4}{\text{(g)}}}&{\Delta {H^\Theta } = + {\text{52 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \\ {{\text{2C(s)}} + {\text{3}}{{\text{H}}_2}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_6}{\text{(g)}}}&{\Delta {H^\Theta } = – {\text{85 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \end{array}\]
What is the enthalpy change, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), for the reaction between ethene and hydrogen?
\[{{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {{\text{H}}_2}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_6}{\text{(g)}}\]
A. –137
B. –33
C. +33
D. +137
▶️Answer/Explanation
A
Here, required equation can be obtained by subtracting equation 1 from equation 2.
Enthalpy change for the required equation = -85 – (+52) = -137