Question
Ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}\), is a base according to both the Brønsted–Lowry and the Lewis theories of acids and bases.
The equation for the reaction between sodium hydroxide, NaOH, and nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}\), is shown below.
\[\begin{array}{*{20}{l}} {{\text{NaOH(aq)}} + {\text{HN}}{{\text{O}}_3}{\text{(aq)}} \to {\text{NaN}}{{\text{O}}_3}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}}}&{{\text{ }}\Delta H = – 57.6{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \end{array}\]
Distinguish between the terms strong base and weak base, and state one example of each.
State the equation for the reaction of ammonia with water.
Explain why ammonia can act as a Brønsted–Lowry base.
Explain why ammonia can also act as a Lewis base.
(i) When ammonium chloride, \({\text{N}}{{\text{H}}_{\text{4}}}{\text{Cl(aq)}}\), is added to excess solid sodium carbonate, \({\text{N}}{{\text{a}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}{\text{(s)}}\), an acid–base reaction occurs. Bubbles of gas are produced and the solid sodium carbonate decreases in mass. State one difference which would be observed if nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), was used instead of ammonium chloride.
(ii) Deduce the Lewis structures of the ammonium ion, \({\text{NH}}_4^ + \), and the carbonate ion, \({\text{CO}}_3^{2 – }\).
Ammonium ion\(\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \)Carbonate ion
(iii) Predict the shapes of \({\text{NH}}_4^ + \) and \({\text{CO}}_3^{2 – }\).
\({\text{NH}}_4^ + \):
\({\text{CO}}_3^{2 – }\):
(i) Sketch and label an enthalpy level diagram for this reaction.
(ii) Deduce whether the reactants or the products are more energetically stable, stating your reasoning.
(iii) Calculate the change in heat energy, in kJ, when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{2.50 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) sodium hydroxide solution is added to excess nitric acid.
When 5.35 g ammonium chloride, \({\text{N}}{{\text{H}}_{\text{4}}}{\text{Cl(s)}}\), is added to \({\text{100.0 c}}{{\text{m}}^{\text{3}}}\) of water, the temperature of the water decreases from 19.30 °C to 15.80 °C. Determine the enthalpy change, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), for the dissolving of ammonium chloride in water.
Answer/Explanation
Markscheme
a strong base: base/electrolyte (assumed to be almost) completely/100% dissociated/ionized (in solution/water) / OWTTE and a weak base: base/electrolyte partially dissociated/ionized (in solution/water) / OWTTE;
example of a strong base: any group I hydroxide / \({\text{Ba(OH}}{{\text{)}}_2}\);
example of a weak base: \({\text{N}}{{\text{H}}_3}\) / \({\text{C}}{{\text{H}}_3}{\text{N}}{{\text{H}}_2}\) / any reasonable answer;
\({\text{N}}{{\text{H}}_3} + {{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{NH}}_4^ + + {\text{O}}{{\text{H}}^ – }\);
accepts a proton/\({{\text{H}}^ + }\) / OWTTE;
donates an electron pair;
(i) more vigorous reaction / more gas bubbles / OWTTE;
more heat released;
solid decreases more quickly;
(ii) 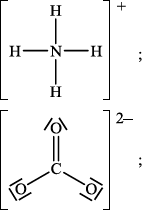
Accept any combination of lines, dots or crosses to represent electron pairs.
(iii) NH4+:
tetrahedral;
CO32–:
trigonal/triangular planar;
(i) enthalpy on y-axis;
Do not accept energy.
reactants higher than products;
\(\Delta H\) labelled;
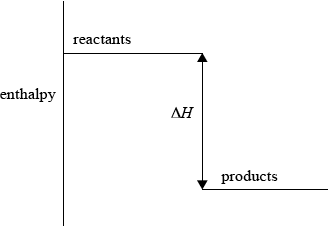
Accept appropriate formulas for reactants and products.
Arrow heads not needed.
57.6 is acceptable as an alternative to \(\Delta H\).
(ii) products are more stable as they are at a lower enthalpy level / energy has been given off by the reactants / reaction is exothermic / OWTTE;
(iii) \(n{\text{(NaOH)}} = 0.125{\text{ mol}}\);
change in heat energy \( = ( – 57.6 \times 0.125) = – 7.20{\text{ (kJ)}}\) / heat released \( = (57.6 \times 0.125) = 7.20{\text{ (kJ)}}\);
\(q = (mc\Delta T = ){\text{ }}100.0 \times 4.18 \times 3.50/1463{\text{ J}}/1460{\text{ J}}\);
\(n{\text{(N}}{{\text{H}}_{\text{4}}}{\text{Cl)}} = \frac{{5.35}}{{53.5}}/0.100{\text{ mol}}\);
\(\Delta H = + 14.6/14.6{\text{ (kJ mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Accept q = 105.35 \( \times \) 4.18 \( \times \) 3.50 / 1541 J.
Accept \(\Delta H\) = +15.4 / 15.4 (kJ\(\,\)mol–1)
Examiners report
Part (a) was answered well although some mentioned “dissolving” instead of “dissociating”.
In (b), the equation was well done.
In (b), the equation was well done as was (ii).
Inevitably, many omitted “pair” in (iii).
Part (c)(i) was generally correct. In (c)(ii) the carbonate ion was legitimately examined under AS 4.2.7; it was not well known – there were too many carbons with expanded octets and oxygens where the lone pairs had been missed. (In the HL specification, the carbonate ion‘s delocalization is considered.) In (iii), however, the shapes were well known.
If there was to be an error made in (d)(i), it was to omit “enthalpy” from the y-axis and some unaccountably put the correct chemicals on the line and then reversed the names products and reactants. The calculations in (d)(iii) inevitably depended on an ability to calculate and think logically.
The calculations in (e) inevitably depended on an ability to calculate and think logically.
Question
To determine the enthalpy change of combustion of methanol, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{OH}}\), 0.230 g of methanol was combusted in a spirit burner. The heat released increased the temperature of \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of water from 24.5 °C to 45.8 °C.
The manufacture of gaseous methanol from CO and \({{\text{H}}_{\text{2}}}\) involves an equilibrium reaction.
\[{\text{CO(g)}} + {\text{2}}{{\text{H}}_2}{\text{(g)}} \rightleftharpoons {\text{C}}{{\text{H}}_3}{\text{OH(g)}}\,\,\,\,\,\Delta {H^\Theta } < 0\]
State and explain the effect of the following changes on the equilibrium position of the reaction in part (c).
Calculate the enthalpy change of combustion of methanol.
Using the theoretical value in Table 12 of the Data Booklet, discuss the experimental results, including one improvement that could be made.
Methanol can be produced according to the following equation.
\[{\text{CO(g)}} + {\text{2}}{{\text{H}}_2}{\text{(g)}} \to {\text{C}}{{\text{H}}_3}{\text{OH(l)}}\]
Calculate the standard enthalpy change of this reaction using the following data:
\[\begin{array}{*{20}{l}} {{\text{I: 2C}}{{\text{H}}_3}{\text{OH(l)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{4}}{{\text{H}}_{\text{2}}}{\text{O(l)}}}&{\Delta {H^\Theta } = – 1452{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \\ {{\text{II: 2CO(g)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}}}&{\Delta {H^\Theta } = – 566{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \\ {{\text{III: 2}}{{\text{H}}_2}{\text{(g)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = – 572{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \end{array}\]
Outline the characteristics of a chemical equilibrium.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for this reaction.
Increase in temperature.
Increase in pressure.
Addition of a catalyst.
Answer/Explanation
Markscheme
\((q = mc\Delta T = ){\text{ }}0.0500 \times 4.18 \times 21.3 = 4.45{\text{ (kJ)}}\);
Do not accept m = 0.05023 kg.
\({\text{(}}n{\text{ }}methanol = {\text{) }}\frac{{0.230}}{{{\text{32.05}}}} = 7.18 \times {10^{ – 3}}{\text{ (mol)}}\);
\(\Delta H = \frac{{4.45}}{{7.18 \times {{10}^{ – 3}}}}\);
\(\Delta H = – 6.20 \times {10^2}{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\);
Accept integer values of molar mass.
Final answer must have negative sign and correct units.
Award [4] for correct final answer with correct units.
less heat is liberated than theoretically/\( – 726{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\);
probably due to heat loss/incomplete combustion;
determine heat capacity of calorimeter and take heat absorbed by calorimeter into account / any suitable insulation method / measure temperature with time and extrapolation of graph to compensate heat loss / OWTTE;
If the value calculated in (a) (i) is more exothermic than theoretically, allow ECF for M1 and for improvement if consistent.
\(\Delta {H^\Theta } = \frac{1}{2}{\text{II}} + {\text{III}} – \frac{1}{2}{\text{I}}\) / correct diagram/energy cycle;
\( – 283 – 572 – ( – 726)\);
\( – 129{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [3] for correct final answer.
rate of forward reaction equals rate of backward reaction;
concentrations of reactants and products do not change / constant macroscopic properties;
\({K_{\text{c}}} = \frac{{{\text{[C}}{{\text{H}}_3}{\text{OH]}}}}{{{\text{[CO][}}{{\text{H}}_2}{{\text{]}}^2}}}\);
Do not award mark if incorrect brackets are used or brackets omitted.
shifts to left/reactants;
to endothermic side / (forward) reaction is exothermic;
shifts to the right/products;
to the side with fewer gas molecules/moles of gas;
no effect on equilibrium;
rate of forward and backward reaction increase equally / activation energy of forward and backward reaction lowered equally;
Examiners report
Many candidates used the mass of methanol in their calculation and most did not convert the mass of methanol to moles.
Students did not make a comparison between their calculated value and the theoretical value, often just stating the numbers. Most candidates were aware that heat was lost but improvements were generally simplistic.
The energy cycle was fairly well done, though working out could be shown better.
Many students had no problem with the characteristics of a chemical equilibrium.
The expression for\({K_{\text{c}}}\) was done quite well.
The effect of changes on the equilibrium position was answered quite well, though candidates had difficulty in explaining the rationale, omitting often gas molecules (ii) and increasing equally in (iii).
The effect of changes on the equilibrium position was answered quite well, though candidates had difficulty in explaining the rationale, omitting often gas molecules (ii) and increasing equally in (iii).
The effect of changes on the equilibrium position was answered quite well, though candidates had difficulty in explaining the rationale, omitting often gas molecules (ii) and increasing equally in (iii).
