Question
Nitrogen monoxide reacts at 1280 °C with hydrogen to form nitrogen and water. All reactants and products are in the gaseous phase.
The gas-phase decomposition of dinitrogen monoxide is considered to occur in two steps.
\[\begin{array}{*{20}{l}} {{\text{Step 1:}}}&{{{\text{N}}_2}{\text{O(g)}}\xrightarrow{{{k_1}}}{{\text{N}}_2}({\text{g)}} + {\text{O(g)}}} \\ {{\text{Step 2:}}}&{{{\text{N}}_2}{\text{O(g)}} + {\text{O(g)}}\xrightarrow{{{k_2}}}{{\text{N}}_2}({\text{g)}} + {{\text{O}}_2}{\text{(g)}}} \end{array}\]
The experimental rate expression for this reaction is rate \( = k{\text{[}}{{\text{N}}_2}{\text{O]}}\).
The conversion of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{NC}}\) into \({\text{C}}{{\text{H}}_{\text{3}}}{\text{CN}}\) is an exothermic reaction which can be represented as follows.
\({\text{C}}{{\text{H}}_{\text{3}}}–{\text{N}}\)\( \equiv \)\({\text{C}} \to {\text{transition state}} \to {\text{C}}{{\text{H}}_{\text{3}}}–{\text{C}}\)\( \equiv \)\({\text{N}}\)
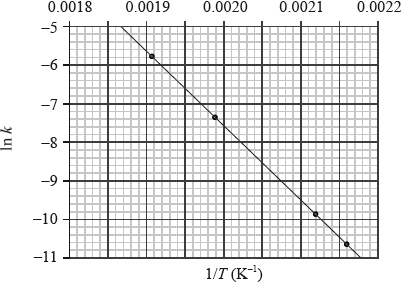
This reaction was carried out at different temperatures and a value of the rate constant, \(k\), was obtained for each temperature. A graph of \(\ln k\) against \(1/T\) is shown below.
Define the term rate of reaction.[1]
State an equation for the reaction of magnesium carbonate with dilute hydrochloric acid.[1]
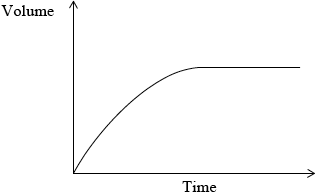
The rate of this reaction in (a) (ii), can be studied by measuring the volume of gas collected over a period of time. Sketch a graph which shows how the volume of gas collected changes with time.[1]
The experiment is repeated using a sample of hydrochloric acid with double the volume, but half the concentration of the original acid. Draw a second line on the graph you sketched in part (a) (iii) to show the results in this experiment. Explain why this line is different from the original line.[4]
The kinetics of the reaction were studied at this temperature. The table shows the initial rate of reaction for different concentrations of each reactant.
Deduce the order of the reaction with respect to NO and \({{\text{H}}_2}\), and explain your reasoning.[4]
Deduce the rate expression for the reaction.[1]
Determine the value of the rate constant for the reaction from Experiment 3 and state its units.[2]
Identify the rate-determining step.[1]
Identify the intermediate involved in the reaction.[1]
Define the term activation energy, \({E_{\text{a}}}\).[1]
Construct the enthalpy level diagram and label the activation energy, \({E_{\text{a}}}\), the enthalpy change, \(\Delta H\), and the position of the transition state.[3]
Describe qualitatively the relationship between the rate constant, \(k\), and the temperature, \(T\).[1]
Calculate the activation energy, \({E_{\text{a}}}\), for the reaction, using Table 1 of the Data Booklet.[4]
Answer/Explanation
Markscheme
decrease in concentration/mass/amount/volume of reactant with time / increase in concentration/mass/amount/volume of product with time / change in concentration/mass/amount/volume of reactant/product with time;
\({\text{MgC}}{{\text{O}}_3}{\text{(s)}} + {\text{2HCl(aq)}} \to {\text{MgC}}{{\text{l}}_2}{\text{(aq)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}}\);
Ignore state symbols.
 ;
;
Plot starts at the origin and levels off.
No mark awarded if axes are not labelled.
new curve reaches same height as original curve;
new curve less steep than original curve;
volume of gas produced is the same because the same amount of acid is used;
reaction is slower because concentration is decreased;
(from experiments 1 and 2 at constant \({\text{[}}{{\text{H}}_2}{\text{]}}\)), [NO] doubles, rate quadruples;
hence, second order with respect to NO;
(from experiments 2 and 3 at constant [NO]), \({\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\)doubles, rate doubles;
first order with respect to \({{\text{H}}_2}\);
Allow alternative mathematical deductions also.
\({\text{rate}} = k{{\text{[NO]}}^{\text{2}}}{\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\);
\(k\left( { = (10.00 \times {{10}^{ – 5}})/{{(10.00 \times {{10}^{ – 3}})}^2}(4.00 \times {{10}^{ – 3}})} \right) = 2.50 \times {10^2}\);
Do not penalize if Experiments 1 or 2 are used to determine k.
\({\text{mo}}{{\text{l}}^{ – 2}}{\text{d}}{{\text{m}}^6}{{\text{s}}^{ – 1}}\);
step 1 / equation showing step 1;
O (atom) / oxygen atom;
Do not allow oxygen or O2.
(minimum) energy needed for a reaction to occur / difference in energy between the reactants and transition state;
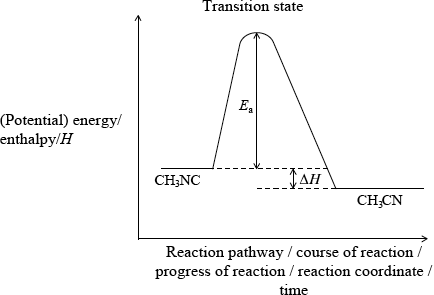
correct position of activation energy;
correct position of \(\Delta H\) and \(H{\text{(C}}{{\text{H}}_3}{\text{NC)}}\)/reactant line above \(H{\text{(C}}{{\text{H}}_3}{\text{CN)}}\) product line;
Accept \(\Delta E\) instead of \(\Delta H\) on diagram if y-axis is labelled as energy.
Do not penalize if CH3NC and CH3CN are not labelled on diagram.
correct position of transition state;
Allow [2 max] if axes are not labelled on diagram.
as temperature/\(T\) increases rate constant/k increases (exponentially);
from graph gradient \(m = – \frac{{{E_{\text{a}}}}}{R}\);
measurement of gradient from chosen points on graph;
Units of m are K. Do not penalize if not given, but do not award mark for incorrect units.
Value of m is based on any two suitable points well separated on the plot.
correct answer for \({E_{\text{a}}}\);
correct units corresponding to answer;
Note: A typical answer for Ea = 1.6 \( \times \) 102 kJ / kJ\(\,\)mol–1.
Examiners report
Surprisingly, the rate of reaction was only correctly defined by approximately 50% of candidates in (a) (i).
The equation for the reaction of magnesium carbonate with dilute hydrochloric acid was not well answered (part (ii)), and often candidates did not write correct formula or forgot to include water as a product.
Part (iii) was well answered by most candidates.
Part (iv) was well answered by most candidates, although the weaker candidates often only scored two or three marks.
Part (b) (i) was well answered and many candidates scored all four marks. Some candidates used a simple mathematical approach and those that followed this method typically were able to deduce the order correctly.
For (ii) most candidates were able to write the rate expression for the reaction.
In (iii), determining the value of the rate constant and its corresponding units was difficult for many candidates and only the better candidates scored both marks. Many mistakes were seen in the units.
Part (c) (i) was usually well answered.
A common mistake for (ii) involved candidates writing \({{\text{O}}_{\text{2}}}\) instead of O.
The definition of activation energy was well answered.
Part (ii) was a question where most candidates scored at least one/two marks although perfect answers were less common. Reasons leading to the loss of marks included: absence of axes, incomplete libelling of axes and the incorrect identification of the position of the transition state.
Parts (iii) and (iv) were very poorly answered for such a fundamental topic. All sorts of errors were evident, including incorrect gradients, inability to rearrange the Arrhenius Equation etc.
Even the better candidates struggled greatly with this question, even though this comes straight from AS 16.3.2.
Question
Consider the following reaction studied at 263 K.
\[{\text{2NO(g)}} + {\text{C}}{{\text{l}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2NOCl(g)}}\]
It was found that the forward reaction is first order with respect to \({\rm{C}}{{\rm{l}}_2}\) and second order with respect to NO. The reverse reaction is second order with respect to NOCl.
Consider the following equilibrium reaction.
\[\begin{array}{*{20}{c}} {{\text{C}}{{\text{l}}_2}({\text{g)}} + {\text{S}}{{\text{O}}_2}({\text{g)}} \rightleftharpoons {\text{S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}({\text{g)}}}&{\Delta {H^\Theta } = – 84.5{\text{ kJ}}} \end{array}\]
In a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) closed container, at 375 °C, \({\text{8.60}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol}}\) of \({\text{S}}{{\text{O}}_{\text{2}}}\) and \({\text{8.60}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol}}\) of \({\text{C}}{{\text{l}}_{\text{2}}}\) were introduced. At equilibrium, \({\text{7.65}} \times {\text{1}}{{\text{0}}^{ – 4}}{\text{ mol}}\) of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\) was formed.
State the rate expression for the forward reaction.[1]
Predict the effect on the rate of the forward reaction and on the rate constant if the concentration of NO is halved.[2]
1.0 mol of \({\rm{C}}{{\rm{l}}_2}\) and 1.0 mol of NO are mixed in a closed container at constant temperature. Sketch a graph to show how the concentration of NO and NOCl change with time until after equilibrium has been reached. Identify the point on the graph where equilibrium is established.[4]
Consider the following reaction.
\[{\text{N}}{{\text{O}}_2}{\text{(g)}} + {\text{CO(g)}} \to {\text{NO(g)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}}\]
Possible reaction mechanisms are:
\(\begin{array}{*{20}{l}} {{\text{Above 775 K:}}}&{{\text{N}}{{\text{O}}_2} + {\text{CO}} \to {\text{NO}} + {\text{C}}{{\text{O}}_{\text{2}}}}&{{\text{slow}}} \\ {{\text{Below 775 K:}}}&{{\text{2N}}{{\text{O}}_2} \to {\text{NO}} + {\text{N}}{{\text{O}}_{\text{3}}}}&{{\text{slow}}} \\ {}&{{\text{N}}{{\text{O}}_3} + {\text{CO}} \to {\text{N}}{{\text{O}}_2} + {\text{C}}{{\text{O}}_2}}&{{\text{fast}}} \end{array}\)
Based on the mechanisms, deduce the rate expressions above and below 775 K.[2]
State two situations when the rate of a chemical reaction is equal to the rate constant.[2]
Consider the following graph of \(\ln k\) against \(\frac{1}{T}\) for the first order decomposition of \({{\text{N}}_{\text{2}}}{{\text{O}}_{\text{4}}}\) into \({\text{N}}{{\text{O}}_{\text{2}}}\). Determine the activation energy in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\) for this reaction.
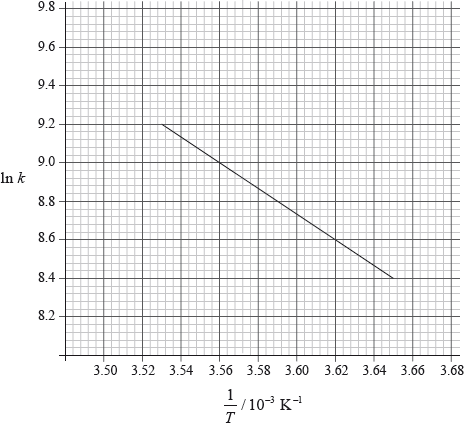 [2]
[2]
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.[1]
Determine the value of the equilibrium constant, \({K_{\text{c}}}\).[3]
If the temperature of the reaction is changed to 300 °C, predict, stating a reason in each case, whether the equilibrium concentration of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\) and the value of \({K_{\text{c}}}\) will increase or decrease.[3]
If the volume of the container is changed to \({\text{1.50 d}}{{\text{m}}^{\text{3}}}\), predict, stating a reason in each case, how this will affect the equilibrium concentration of \({\text{S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}\) and the value of \({K_{\text{c}}}\).[3]
Suggest, stating a reason, how the addition of a catalyst at constant pressure and temperature will affect the equilibrium concentration of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\).[2]
Answer/Explanation
Markscheme
\({\text{rate}} = k{{\text{[NO]}}^2}{\text{[C}}{{\text{l}}_{\text{2}}}{\text{]}}\);
rate of reaction will decrease by a factor of 4;
no effect on the rate constant;
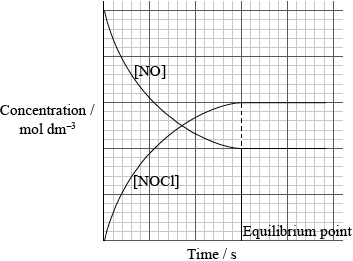
y axis labelled concentration/\({\text{mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) and x axis is labelled time/s;
gradient for [NO];
gradient for [NOCl] will be equal and opposite;
equilibrium point identified / two curves level off at same time;
Above 775 K: \({\text{rate}} = k{\text{[N}}{{\text{O}}_2}{\text{][CO]}}\);
Below 775 K: \({\text{rate}} = k{{\text{[N}}{{\text{O}}_2}{\text{]}}^2}\);
zero order reaction;
all concentrations are \({\text{1.0 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
\({\text{slope}} = \frac{{9.2 – 8.4}}{{(3.53 – 3.65) \times {{10}^{ – 3}}}} = – 6.67 \times {10^3}\);
\(({E_{\text{a}}} = 6.67 \times {10^3} \times 8.31)\)
\({\text{55.4 (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Accept in range 55.0 – 56.0
Award [1] if 55454 (J) stated
Award [2] for the correct final answer
\(({K_{\text{c}}}) = \frac{{{\text{[S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}{\text{]}}}}{{{\text{[C}}{{\text{l}}_2}{\text{][S}}{{\text{O}}_2}{\text{]}}}}\);
Ignore state symbols.
Square brackets [ ] required for the equilibrium expression.
\({\text{7.84}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol of S}}{{\text{O}}_2}\) and \({\text{7.84}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol of C}}{{\text{l}}_2}\);
\({\text{7.84}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{ of S}}{{\text{O}}_2}\), \({\text{7.84}} \times {\text{1}}{{\text{0}}^{ – 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{ of C}}{{\text{l}}_2}\) and
\({\text{7.65}} \times {\text{1}}{{\text{0}}^{ – 4}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{ of S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}\);
12.5;
Award [1] for 10.34
Award [3] for the correct final answer
value of \({K_{\text{c}}}\) increases;
\({\text{[S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}{\text{]}}\) increases;
decrease in temperature favours (forward) reaction which is exothermic;
Do not allow ECF.
no effect on the value of \({K_{\text{c}}}\) / depends only on temperature;
\({\text{[S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}{\text{]}}\) decreases;
increase in volume favours the reverse reaction which has more gaseous moles;
Do not allow ECF.
no effect;
catalyst increases the rate of forward and reverse reactions (equally) / catalyst decreases activation energies (equally);
Examiners report
In part (a) the rate expression was correctly stated although some confused this with an equilibrium constant expression.
Only the better candidates realized that the rate of reaction will decrease by a factor of four and there will be no effect on the rate constant.
Although most candidates were able to correctly sketch the concentration versus time graph many forgot to label the axes or include units.
Part (b) was well answered and candidates demonstrated a good understanding of rate expressions based on reaction mechanism.
The better candidates were able to figure out that the rate of a chemical reaction is equal to the rate constant when all concentrations are \({\text{1.0 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) or for a zero order reaction.
Most candidates had difficulty in calculating activation energy from the graph in part (d) and some gave the answer in \({\text{J}}\,{\text{mo}}{{\text{l}}^{ – 1}}\) instead of \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\) which showed that they missed this instruction in the question.
In part (e), the equilibrium constant expression was correctly stated by the majority but calculating the value of\({K_{\text{c}}}\) proved to be difficult.
A large number of candidates obtained the incorrect answer of 10.34 as a result of using the initial concentrations of the reactants instead of equilibrium concentrations.
[N/A]
The application of Le Chatelier’s principle was handled well by the majority with minor omissions such as not using the term gaseous particles in part (iv).
Some candidates stated that the addition of a catalyst does not affect the value of \({K_{\text{c}}}\) or the position of equilibrium, which did not answer the question and scored no marks because they had not commented on the concentration of \({\text{SOC}}{{\text{l}}_{\text{2}}}\). Some candidates correctly stated that a catalyst increases the rate of forward and reverse reactions equally.