Question
There has been significant growth in the use of carbon nanotubes, CNT.
a. Explain these properties of carbon nanotubes.

b(i)CNT can act as Type 2 superconductors. Outline why Type 2 superconductors are generally more useful than Type 1.
b(iiExplain the role of electrons in superconducting materials in terms of the Bardeen-Cooper-Schrieffer (BCS) theory.
c(i)Alloying metals changes their properties. Suggest one property of magnesium that could be improved by making a magnesium-CNT alloy.
c(ii). Pure magnesium needed for making alloys can be obtained by electrolysis of molten magnesium chloride.
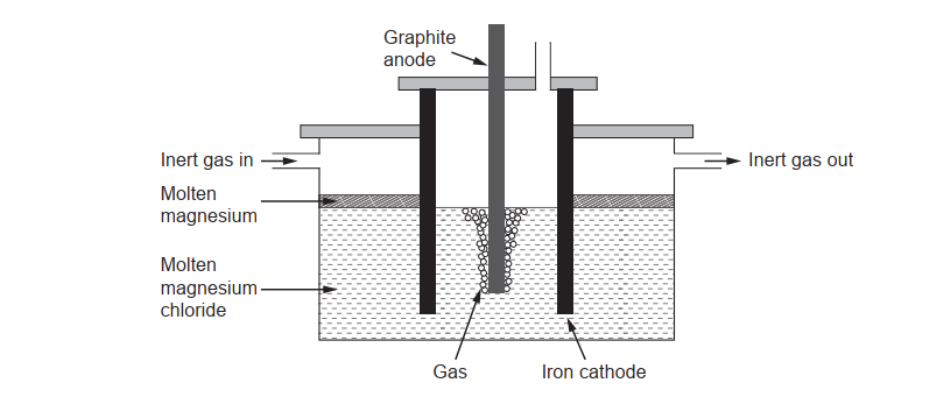
Calculate the theoretical mass of magnesium obtained if a current of $3.00 \mathrm{~A}$ is used for 10.0 hours. Use charge $:(Q)=c u r r e n t(l) \times$ time $(t)$ and section 2 of the data booklet.
c(iiiluggest a gas which should be continuously passed over the molten magnesium in the electrolytic cell.
d. Zeolites can be used as catalysts in the manufacture of CNT. Explain, with reference to their structure, the high selectivity of zeolites.
e. Experiments have been done to explore the nematic liquid crystal behaviour of CNT. Justify how CNT molecules could be classified as nematic.
▶️Answer/Explanation
Markscheme
a. Excellent strength: defect-free AND rigid/regular 2D/3D
Excellent conductivity: delocalized electrons
Accept “carbons/atoms are all covalently bonded to each other” for M1.
b(i)Any two of:
have higher critical temperatures $/ T_{\mathrm{c}}$ «than Type 1»
OR
can act at higher temperatures
have higher critical magnetic fields $/ B_c$ «than Type 1 »
less time needed to cool to operating temperature
less energy required to cool down/maintain low temperature
b(ii)Any three of:
passing electrons «slightly» deform lattice/displace positive ions/cations electrons couple/form Cooper pairs/condense with other electrons energy propagates along the lattice in wave-like manner/as phonons Cooper pair/electron condensate/pair of electrons moves through lattice freely OR phonons are «perfectly» elastic/cause no energy loss
c(i)Any of:
ductility
strength/resistance to deformation
malleability
hardness
resistance to corrosion/chemical resistance
range of working temperatures $\checkmark$
density
Do not accept “conductivity”.
$$
\begin{gathered}
\mathrm{c}(\mathrm{ii}) « Q=I \times t=3.00 \times 10.0 \times 3600=» 108000 \mathrm{C} \\
« \frac{Q}{F}=\frac{108000 \mathrm{C}}{96500 \mathrm{C} \mathrm{mol}^{-1}}=» 1.12\left\langle\mathrm{~mol} \mathrm{e}^{-} »\right. \\
« \frac{1.12 \mathrm{~mol}}{2}=0.560 \mathrm{~mol} \mathrm{Mg} » \\
« m=0.560 \mathrm{~mol} \times 24.31 \mathrm{~g} \mathrm{~mol}-1=» 13.6 \ll \mathrm{g} »
\end{gathered}
$$
Award [3] for correct final answer.
c(iii)Argon/Ar/helium/He
Accept any identified noble/inert gas.
Accept name OR formula.
Do not accept “nitrogen/ $\mathrm{N}_2$ “.
d. pores/cavities/channels/holes/cage-like structures
«only» reactants with appropriate/specific size/geometry/structure fit inside/go through/are activated/can react Accept “molecules/ions” for “reactants” in M2.
e. rod-shaped molecules
OR
«randomly distributed but» generally align
OR
no positional order AND have «some» directional order/pattern
Accept “linear” for “rod-shaped”.
Question
Vanadium forms a body centred cubic (BCC) crystal structure with an edge length of $303 \mathrm{pm}$, $\left(303 \times 10^{-12} \mathrm{~m}\right)$.
a.i. Deduce the number of atoms per unit cell in vanadium.
a.ii.Calculate the expected first order diffraction pattern angle, in degrees, if $x$-rays of wavelength $150 \mathrm{pm}$ are directed at a crystal of vanadium.
Assume the edge length of the crystal to be the same as separation of layers of vanadium atoms found by $x$-ray diffraction. Use section 1 of the data booklet.
a.iiiCalculate the average mass, in $\mathrm{g}$, of a vanadium atom by using sections 2 and 6 of the data booklet.
a.ivDetermine the volume, in $\mathrm{cm}^3$, of a vanadium unit cell.
a.v.Determine the density, in $\mathrm{g} \mathrm{cm}^{-3}$, of vanadium by using your answers to (a)(i), (a)(iii) and (a)(iv).
b.i.Vanadium and other transition metals can interfere with cell metabolism.
State and explain one process, other than by creating free radicals, by which transition metals interfere with cell metabolism.
b.ii.Vanadium(IV) ions can create free radicals by a Fenton reaction.
Deduce the equation for the reaction of $\mathrm{V}^{4+}$ with hydrogen peroxide.
▶️Answer/Explanation
Markscheme
a.i. 2
[1 mark]
a.ii $n \wedge=2 d \sin \theta$
OR
$\theta=\sin ^{-1}\left(\frac{\mathrm{n} \lambda}{2 \mathrm{~d}}\right)$
$\theta=« \sin ^{-1}\left(\frac{150}{2 \times 303}\right)=» 14.3$ « $^{\circ} »$
Award [2] for correct final answer.
[2 marks]
a.iiim $=\varkappa \frac{50.94}{6.02 \times 10^{23}}=» 8.46 \times 10^{-23} « \mathrm{~g} »$
[1 mark]
a.iv $303 \mathrm{pm}=303 \times 10^{-10} \mathrm{cm»}$
[1 mark]
a.v.« $8.46 \times 10^{-23} \mathrm{~g} \times 2=» 1.69 \times 10^{-22} « \mathrm{~g} »$
$$
d=« \frac{1.69 \times 10^{-22} \mathrm{~g}}{2.78 \times 10^{-23} \mathrm{~cm}^3}=» 6.08 \approx \mathrm{g} \mathrm{cm}^{-3} »
$$
Accept any value in the range $6.07-6.09 \mathrm{rg} \mathrm{cm}^{-3} \mathrm{»}$.
Award [2] for correct final answer.
[2 marks]
b.i. Any one of these alternatives:
ALTERNATIVE 1
disrupt enzyme binding sites
which can inhibit/over-stimulate enzymes
ALTERNATIVE 2
disrupt endocrine system
because they compete for active sites of enzymes/cellular receptors
ALTERNATIVE 3
form complexes/coordination compounds
which can bind to enzymes
ALTERNATIVE 4
act as oxidizing/reducing agents
OR
act as catalysts
which can initiate unwanted reactions
Accept “can undergo oxidation-reduction reactions” for M1 in Alternative 4.
[2 marks]
b.ii. $\mathrm{V}^{4+}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}_2(\mathrm{aq}) \rightarrow \mathrm{V}^{5+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})+\cdot \cdot \mathrm{OH}(\mathrm{aq})$
Do not accept • on $\mathrm{H}$.
Accept answer without $\cdot$
[1 mark]
Question
\text { A representation of the unit cell of gold is shown. }
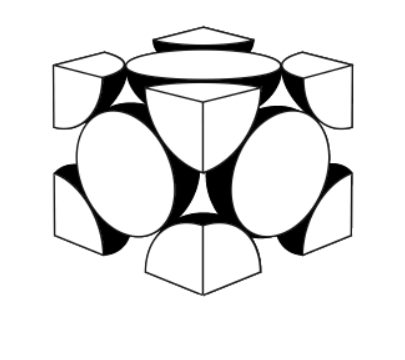
a.i. State the name of the crystal structure of gold.
a.ii.Calculate the number of atoms per unit cell of gold, showing your working.
b. The edge length of the gold unit cell is $4.08 \times 10^{-8} \mathrm{~cm}$.
Determine the density of gold in $\mathrm{g} \mathrm{cm}^{-3}$, using sections 2 and 6 of the data booklet.
▶️Answer/Explanation
Markscheme
a.i.face-centred cube/fcc
OR
cubic close packed/ccp
a.ii. $\frac{1}{2}$ «atom per face» $\times 6$ «faces per cube» $\times 3$ «atoms» $A N D \frac{1}{8}$ «atom per corner» $\times 8$ «corners per cube» $=1$ «atom» «atoms per unit cell $=3+1=» 4$
Award [1 max] for “4” without working shown.
b. «4 atoms per unit cell»
mass of 4 atoms $«=4 \times \frac{196.97 \mathrm{~g} \mathrm{~mol}^{-1}}{6.02 \times 10^{23} \mathrm{~mol}^{-1}}=» 1.31 \times 10^{-21} « \mathrm{~g} »$
volume of unit cell $«=\left(4.08 \times 10^{-8}\right)^3 \mathrm{~cm}^3 »=6.79 \times 10^{-23} « \mathrm{~cm}^3 »$
density $=$ « $\frac{1.31 \times 10^{-21} \mathrm{~g}}{6.79 \times 10^{-23} \mathrm{~cm}^3} »=1.93 \times 10^1 / 19.3$ “g cm$^{-3} »$
Award [3] for correct final answer.
Question
Lithium has many uses.
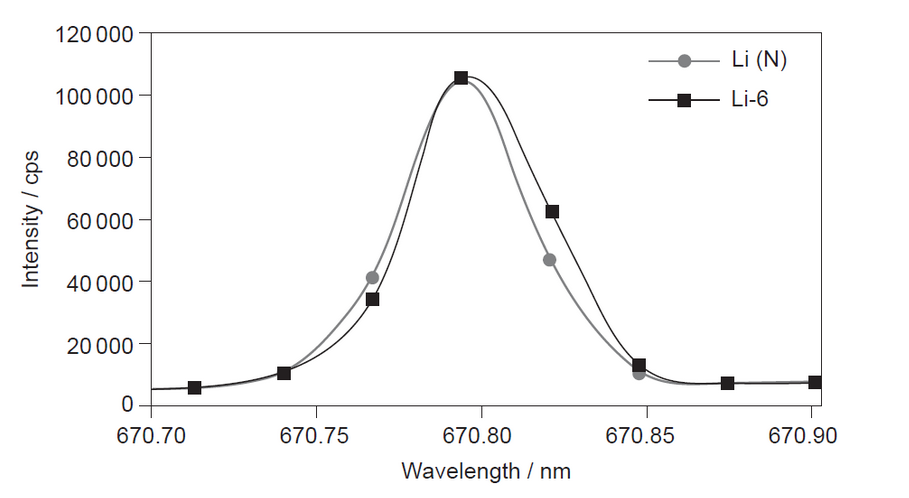
The emission spectra obtained by ICP-OES for a mixture containing the isotope ${ }^6 \mathrm{Li}(\mathrm{Li}-6)$ and naturally occurring lithium (Li (N)) is shown.
a. Identify the type of bonding in lithium hydride, using sections 8 and 29 of the data booklet.
b(i)ldentify the colour of the emission spectrum of lithium using section 17 of the data booklet.
b(ii) Suggest why ICP-OES does not give good quantitative results for distinguishing ${ }^6$ Li from naturally occurring lithium.
b(iii\$uggest a better method.
c. Lithium is obtained by electrolysis of molten lithium chloride. Calculate the time, in seconds, taken to deposit $0.694 \mathrm{~g} \mathrm{Li}$ using a current of $2.00 \mathrm{~A}$.
$$
Q(\text { charge })=I(\text { current }) \times t \text { (time })
$$
$\mathrm{d}(\mathrm{i})$ Lithium has shown some superconductive properties when doped into graphene or when under high pressure. Under high pressure, however, the
Meissner effect is absent.
Describe the Meissner effect.
d(ii)At very low temperatures, lithium atoms enhance the phonon binding of electrons in graphene suggesting the formation of Cooper pairs.
Explain how Cooper pairs are formed.
e. Lithium forms a crystalline lattice with the unit cell structure shown below.
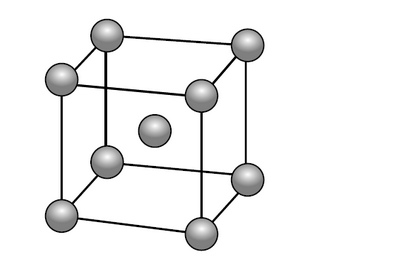
X-ray diffraction shows that the length of the edge of the unit cell is $3.51 \times 10^{-8} \mathrm{~cm}$.
Determine the density of lithium, in $\mathrm{g} \mathrm{cm}^{-3}$, using sections 2 and 6 of the data booklet.
▶️Answer/Explanation
Markscheme
a. ionic [
b(i)red [ $/]$
b(iiemission spectra of both « ${ }^6 \mathrm{Li}$ and natural Li» give same colour/produce same «range of» wavelengths
OR
they have same electron transitions/same nuclear charge $[\mathcal{~}]$
Note: Accept “the spectra are almost identical”.
b(iii)CP-MS [
Note: Accept “MS/mass spectrometry”.
$$
\begin{aligned}
& \text { « } \mathrm{t}=\frac{0.100 \mathrm{~mol} \times 96500 \mathrm{C} \mathrm{mol}^{-1}}{2.00 \mathrm{C} \mathrm{s}^{-1}} » \\
& 4830 \text { «s»[/]}
\end{aligned}
$$
$\mathrm{d}(\mathrm{i})$ creation of mirror image/opposing magnetic field of external field «below critical temperature/T of superconductor»
OR
expulsion of magnetic field from superconductor «below critical temperature/T» [ $[\boldsymbol{]}$
$\mathrm{d}(\mathrm{ii})$ Any three of:
positive ions/cations in lattice are attracted to passing electron [ [ ]
lattice is distorted «by this passing electron» $[\boldsymbol{\sim}]$
creates «local» regions of increased positive charge $\quad[\boldsymbol{}]$
second electron is attracted to deformation AND a coupling occurs $[\boldsymbol{L}$
e. mass of $\mathrm{Li}$ in unit cell $=« 2 \times \frac{6.94 \mathrm{~g} \mathrm{~mol}^{-1}}{6.02 \times 10^{23} \mathrm{~mol}^{-1}} » 2.31 \times 10^{-23} \mathrm{~g} \quad$ [ ]
volume of unit cell $=«\left(3.51 \times 10^{-8} \mathrm{~cm}\right)^3=» 4.32 \times 10^{-23} \mathrm{~cm}^3 \quad$ [/]
«density $=\frac{2.31 \times 10^{-23} \mathrm{~g}}{4.32 \times 10^{-23} \mathrm{~cm}^3}=0.535 \ll \mathrm{g} \mathrm{cm}^{-3} » \quad[/]$
Note: Award [3] for correct final answer.
Question
Superconductivity has many applications.
a. State what is meant by a superconductor.
b. Outline the difference in behaviour of Type 1 and Type 2 superconductors when the temperature is lowered.
▶️Answer/Explanation
Markscheme
a. «material with» no electrical resistance [ $\boldsymbol{D}$
b. Type 1 has sharper transition to superconductivity [ $\checkmark]$
Note: Accept annotated plot of electrical resistance against temperature.
Question
This question is about global warming.
a. Describe the effect of infrared (IR) radiation on carbon dioxide molecules.
b. Outline one approach to controlling industrial emissions of carbon dioxide.
▶️Answer/Explanation
Markscheme
a. bond length $/ \mathrm{C}=\mathrm{O}$ distance changes
OR
«asymmetric» stretching «of bonds»
OR
bond angle/OCO changes $[\boldsymbol{U}]$
polarity/dipole «moment» changes
OR
dipole «moment» created «when molecule absorbs $\mathbb{R}$ » $[\boldsymbol{V}]$
Note: Accept appropriate diagrams.
b. Any one of:
capture where produced «and store» $[\boldsymbol{}]$
use scrubbers to remove $[\boldsymbol{\sim}]$
use as feedstock for synthesising other chemicals $[\boldsymbol{\sim}]$
carbon credit/tax/economic incentive/fines/country specific action [ $\boldsymbol{\nu}$ ]
use alternative energy
OR
stop/reduce use of fossil fuels for producing energy $[\boldsymbol{} \boldsymbol{]}$
use carbon reduced fuels «such as methane» $[\boldsymbol{\sim}]$
increase efficiency and reduce energy use $[\boldsymbol{\sim}]$
Note: Do not accept “planting more trees”.
Accept specific correct examples.
Question
\text { Calcium has a face-centred cubic (cubic close packing) arrangement of atoms. }
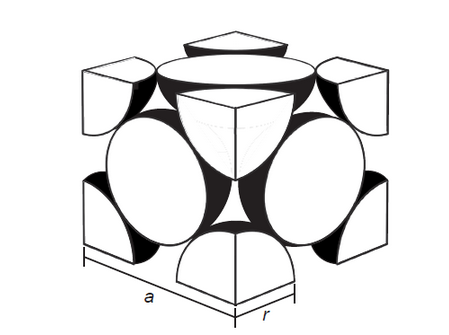
$a=$ unit cell dimension, $r=$ metallic radius
a. State the number of atoms in the unit cell.
b. Determine the density of calcium, in $\mathrm{g} \mathrm{cm}^{-3}$, using section 2 of the data booklet.
$\mathrm{Ar}=40.08 ;$ metallic radius $(\mathrm{r})=1.97 \times 10^{-10} \mathrm{~m}$
▶️Answer/Explanation
Markscheme
a. $« 8 \times \frac{1}{8}+6 \times \frac{1}{2}=» 4[\mathrm{~V}]$
b. $a=« \frac{4 \mathrm{r}}{\sqrt{2}}=\frac{4 \times 1.97 \times 10^{-10} \mathrm{~m}}{\sqrt{2}}=» 5.572 \times 10^{-10} « \mathrm{~m} »$
OR
volume of unit cell $=«\left(5.572 \times 10^{-10} \mathrm{~m}\right)^3 \times 10^6=» 1.73 \times 10^{-22} « \mathrm{~cm}^3 »[\boldsymbol{V}]$
mass of unit cell $=« \frac{40.08 \mathrm{~g} \mathrm{~mol}^{-1} \times 4}{6.02 \times 10^{23} \mathrm{~mol}^{-1}}=» 2.66 \times 10^{-22} « \mathrm{~g} »[\boldsymbol{V}]$
density = « $\frac{2.66 \times 10^{-22} \mathrm{~g}}{\left(5.572 \times 10^{-10}\right)^3 \times 10^6} » 1.54$ « cm$^{-3} »[\boldsymbol{V}]$
Note: Award [3] for correct final answer.
Question
Superconductors have no resistance below a critical temperature.
a(i)Outline how resistance to electric currents occurs in metals.
a(ii)Suggest why the resistance of metals increases with temperature.
b. State two differences between Type I and Type II superconductors.
▶️Answer/Explanation
Markscheme
a(i)electrons collide with cations/positive ions
a(ii)ncreased vibrations of «lattice» ions
increased «probability of» collisions «between electrons and cations»
NOTE: Accept “increases lattice vibrations” for M1.
b. Any two of:
Type I have sharper transitions to superconductivity «than Type II»
Type I have lower critical/operating temperatures «than Type Il»
Type I have lower critical magnetic field «strength than Type Il»
Type I carry lower currents «than Type Il»
Type I are «pure» metals/metalloids AND Type II are alloys/metal oxide ceramics/perovskites/metallic compounds
Type II exist in a mixed state/are partly permeable to the magnetic field AND Type I do not/are not
Question
\text { X-ray crystallography of a metal crystal produces a diffraction pattern of bright spots. }

Using X-rays of wavelength $1.54 \times 10^{-10} \mathrm{~m}$, the first bright spots were produced at an angle $\theta$ of $22.3^{\circ}$ from the centre.
Calculate the separation between planes of atoms in the lattice, in meters, using section 1 of the data booklet.
▶️Answer/Explanation
Markscheme
$$
« d=\frac{\mathrm{n} \lambda}{2 \sin \theta} »
$$
$$
d=« \frac{1 \times 1.54 \times 10^{-10} \mathrm{~m}}{2 \times \sin 22.3^{\circ}} \rrbracket 2.03 \times 10^{-10} « \mathrm{~m} »
$$
