Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .
Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
In a population of rabbits, \(1\%\) are known to have a particular disease. A test is developed for the disease that gives a positive result for a rabbit that does have the disease in \(99\%\) of cases. It is also known that the test gives a positive result for a rabbit that does not have the disease in \(0.1\%\) of cases. A rabbit is chosen at random from the population.
Find the probability that the rabbit tests positive for the disease.
Given that the rabbit tests positive for the disease, show that the probability that the rabbit does not have the disease is less than 10 %.
Answer/Explanation
Markscheme
R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
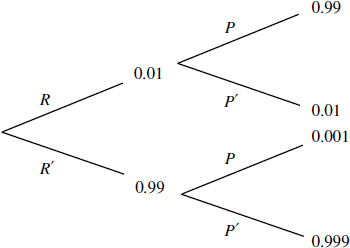
\({\text{P}}(P) = P(R \cap P) + P(R’ \cap P)\)
\( = 0.01 \times 0.99 + 0.99 \times 0.001\) M1
\( = 0.01089( = 0.0109)\) A1
Note: Award M1 for a correct tree diagram with correct probability values shown.
[2 marks]
R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
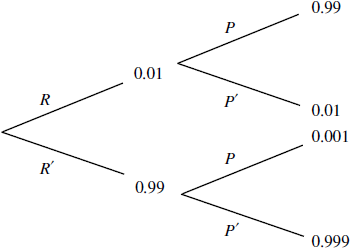
\(P(R’|P) = \frac{{0.001 \times 0.99}}{{0.001 \times 0.99 + 0.01 \times 0.99}}\left( { = \frac{{0.00099}}{{0.01089}}} \right)\) M1A1
\(\frac{{0.00099}}{{0.01089}} < \frac{{0.001}}{{0.01}} = 10\% \) (or other valid argument) R1
[3 marks]
Examiners report
There was a mixed performance in this question with some candidates showing good understanding of probability and scoring well and many others showing no understanding of conditional probability and difficulties in working with decimals. Very few candidates were able to provide a valid argument to justify their answer to part (b).
There was a mixed performance in this question with some candidates showing good understanding of probability and scoring well and many others showing no understanding of conditional probability and difficulties in working with decimals. Very few candidates were able to provide a valid argument to justify their answer to part (b).
Question
In a particular city 20 % of the inhabitants have been immunized against a certain disease. The probability of infection from the disease among those immunized is \(\frac{1}{{10}}\), and among those not immunized the probability is \(\frac{3}{4}\). If a person is chosen at random and found to be infected, find the probability that this person has been immunized.
Answer/Explanation
Markscheme
tree diagram (M1)
\({\text{P(I|D)}} = \frac{{{\text{P(D|I)}} \times {\text{P(I)}}}}{{{\text{P(D)}}}}\) (M1)
\( = \frac{{0.1 \times 0.2}}{{0.1 \times 0.2 + 0.8 \times 0.75}}\) A1A1A1
\(\left( { = \frac{{0.02}}{{0.62}}} \right) = \frac{1}{{31}}\) A1
Note: Alternative presentation of results: M1 for labelled tree; A1 for initial branching probabilities, 0.2 and 0.8; A1 for at least the relevant second branching probabilities, 0.1 and 0.75; A1 for the ‘infected’ end-point probabilities, 0.02 and 0.6; M1A1 for the final conditional probability calculation.
[6 marks]
Examiners report
Candidates who drew a tree diagram, the majority, usually found the correct answer.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
Draw a tree diagram to represent these events and their outcomes.
What is the probability that the “Tigers” soccer team wins?
Given that the “Tigers” soccer team won, what is the probability that it rained on that day?
Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”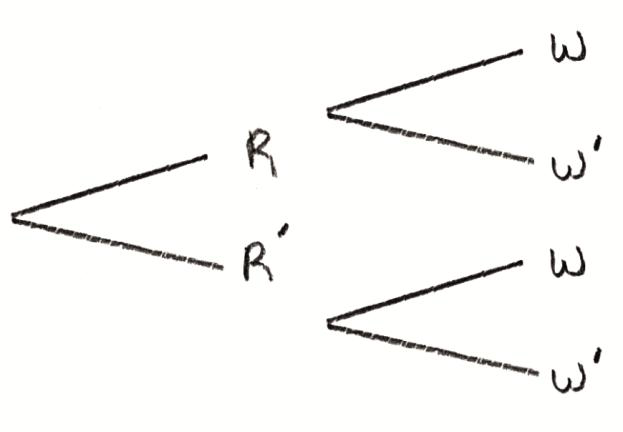 A1
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
Two events A and B are such that \({\text{P}}(A \cup B) = 0.7\) and \({\text{P}}(A|B’) = 0.6\).
Find \({\text{P}}(B)\).
Answer/Explanation
Markscheme
Note: Be aware that an unjustified assumption of independence will also lead to P(B) = 0.25, but is an invalid method.
METHOD 1
\({\text{P}}(A’|B’) = 1 – {\text{P}}(A|B’) = 1 – 0.6 = 0.4\) M1A1
\({\text{P}}(A’|B’) = \frac{{{\text{P}}(A’ \cap B’)}}{{{\text{P}}(B’)}}\)
\({\text{P}}(A’ \cap B’) = {\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
\(0.4 = \frac{{0.3}}{{{\text{P}}(B’)}} \Rightarrow {\text{P(}}B’) = 0.75\) (M1)A1
\({\text{P}}(B) = 0.25\) A1
(this method can be illustrated using a tree diagram)
[6 marks]
METHOD 2
\({\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
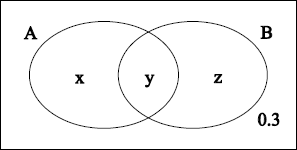
\({\text{P}}(A|B’) = \frac{x}{{x + 0.3}} = 0.6\) M1A1
\(x = 0.6x + 0.18\)
\(0.4x = 0.18\)
\(x = 0.45\) A1
\({\text{P}}(A \cup B) = x + y + z\)
\({\text{P}}(B) = y + z = 0.7 – 0.45\) (M1)
\( = 0.25\) A1
[6 marks]
METHOD 3
\(\frac{{{\text{P}}(A \cap B’)}}{{{\text{P}}(B’)}} = 0.6{\text{ (or P}}(A \cap B’) = 0.6{\text{P}}(B’)\) M1
\({\text{P}}(A \cap B’) = {\text{P}}(A \cup B) – {\text{P}}(B)\) M1A1
\({\text{P}}(B’) = 1 – {\text{P}}(B)\)
\(0.7 – {\text{P}}(B) = 0.6 – 0.6{\text{P}}(B)\) M1(A1)
\(0.1 = 0.4{\text{P}}(B)\)
\({\text{P}}(B) = \frac{1}{4}\) A1
[6 marks]
Examiners report
There is a great variety of ways to approach this question and there were plenty of very good solutions produced, all of which required an insight into the structure of conditional probability. A few candidates unfortunately assumed independence and so did not score well.
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = \frac{2}{5},{\text{ P}}(B) = \frac{{11}}{{20}}\) and \({\text{P}}(A|B) = \frac{2}{{11}}\).
(a) Find \({\text{P}}(A \cap B)\).
(b) Find \({\text{P}}(A \cup B)\).
(c) State with a reason whether or not events \(A\) and \(B\) are independent.
Answer/Explanation
Markscheme
(a) \({\text{P}}(A \cap B) = {\text{P}}(A|B) \times P(B)\)
\({\text{P}}(A \cap B) = \frac{2}{{11}} \times \frac{{11}}{{20}}\) (M1)
\( = \frac{1}{{10}}\) A1
[2 marks]
(b) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\({\text{P}}(A \cup B) = \frac{2}{5} + \frac{{11}}{{20}} – \frac{1}{{10}}\) (M1)
\( = \frac{{17}}{{20}}\) A1
[2 marks]
(c) No – events A and B are not independent A1
EITHER
\({\text{P}}(A|B) \ne {\text{P}}(A)\) R1
\(\left( {\frac{2}{{11}} \ne \frac{2}{5}} \right)\)
OR
\({\text{P}}(A) \times {\text{P}}(B) \ne {\text{P}}(A \cap B)\)
\(\frac{2}{5} \times \frac{{11}}{{20}} = \frac{{11}}{{50}} \ne \frac{1}{{10}}\) R1
Note: The numbers are required to gain R1 in the ‘OR’ method only.
Note: Do not award A1R0 in either method.
[2 marks]
Total [6 marks]
Examiners report
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.2\) and \({\text{P}}(B) = 0.5\).
Determine the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Determine the range of possible values of \({\text{P}}\left( {A|B} \right)\).
Answer/Explanation
Markscheme
(i) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5\)
\( = 0.7\) A1
(ii) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5 – 0.1\)
\( = 0.6\) A1
[4 marks]
\({\text{P}}\left( {A|B} \right) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
\({\text{P}}\left( {A|B} \right)\) is a maximum when \({\text{P}}(A \cap B) = {\text{P}}(A)\)
\({\text{P}}\left( {A|B} \right)\) is a minimum when \({\text{P}}(A \cap B) = 0\)
\(0 \le {\text{P}}\left( {A|B} \right) \le 0.4\) A1A1A1
Note: A1 for each endpoint and A1 for the correct inequalities.
[3 marks]
Total [7 marks]
Examiners report
This part was generally well done.
Disappointingly, many candidates did not seem to understand the meaning of the word ‘range’ in this context.
Question
Two events \(A\) and \(B\) are such that \({\text{P}}(A \cap B’) = 0.2\) and \({\text{P}}(A \cup B) = 0.9\).
On the Venn diagram shade the region \(A’ \cap B’\).
Find \({\text{P}}(A’|B’)\).
Answer/Explanation
Markscheme
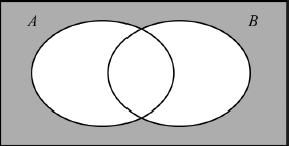 A1
A1
[1 mark]
\(P(A’|B’) = \frac{{P(A’ \cap B’)}}{{P(B’)}}\) (M1)
\(P(B’) = 0.1 + 0.2 = 0.3\) (A1)
\(P(A’ \cap B’) = 0.1\) (A1)
\(P(A’|B’) = \frac{{0.1}}{{0.3}} = \frac{1}{3}\) A1
[4 marks]
Examiners report
Part (a) was well done.
In part (b) some candidates were unable to write down the conditional probability formula. Some then failed to realise that part (a) was designed to help them work out \(P(A’ \cap B’)\) and instead incorrectly assumed independence.
Question
\(A\) and \(B\) are independent events such that \({\text{P}}(A) = {\text{P}}(B) = p,{\text{ }}p \ne 0\).
Show that \({\text{P}}(A \cup B) = 2p – {p^2}\).
Find \({\text{P}}(A|A \cup B)\) in simplest form.
Answer/Explanation
Markscheme
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = p + p – {p^2}\) A1
\( = 2p – {p^2}\) AG
[2 marks]
\({\text{P}}(A|A \cup B) = \frac{{{\text{P}}\left( {A \cap (A \cup B)} \right)}}{{{\text{P}}(A \cup B)}}\) (M1)
Note: Allow \({\text{P}}(A \cap A \cup B)\) if seen on the numerator.
\( = \frac{{{\text{P}}(A)}}{{{\text{P}}(A \cup B)}}\) (A1)
\( = \frac{p}{{2p – {p^2}}}\) A1
\( = \frac{1}{{2 – p}}\) A1
[4 marks]
Examiners report
Part (a) posed few problems. Part (b) was possibly a good discriminator for the 4/5 candidates. Some were aware of an alternative (useful) form for the conditional probability, but were unable to interpret \(P\left( {A \cap (A \cup B)} \right)\). Large numbers of fully correct answers were seen.
Part (a) posed few problems. Part (b) was possibly a good discriminator for the 4/5 candidates. Some were aware of an alternative (useful) form for the conditional probability, but were unable to interpret \(P\left( {A \cap (A \cup B)} \right)\). Large numbers of fully correct answers were seen.
Question
Consider two events \(A\) and \(A\) defined in the same sample space.
Given that \({\text{P}}(A \cup B) = \frac{4}{9},{\text{ P}}(B|A) = \frac{1}{3}\) and \({\text{P}}(B|A’) = \frac{1}{6}\),
Show that \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(A’ \cap B)\).
(i) show that \({\text{P}}(A) = \frac{1}{3}\);
(ii) hence find \({\text{P}}(B)\).
Answer/Explanation
Markscheme
METHOD 1
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) M1
\( = {\text{P}}(A) + {\text{P}}(A \cap B) + {\text{P}}(A’ \cap B) – {\text{P}}(A \cap B)\) M1A1
\( = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) AG
METHOD 2
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) M1
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A|B) \times {\text{P}}(B)\) M1
\( = {\text{P}}(A) + \left( {1 – {\text{P}}(A|B)} \right) \times {\text{P}}(B)\)
\( = {\text{P}}(A) + {\text{P}}(A’|B) \times {\text{P}}(B)\) A1
\( = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) AG
[3 marks]
(i) use \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) and \({\text{P}}(A’ \cap B) = {\text{P}}(B|A’){\text{P}}(A’)\) (M1)
\(\frac{4}{9} = {\text{P}}(A) + \frac{1}{6}\left( {1 – {\text{P}}(A)} \right)\) A1
\(8 = 18{\text{P}}(A) + 3\left( {1 – {\text{P}}(A)} \right)\) M1
\({\text{P}}(A) = \frac{1}{3}\) AG
(ii) METHOD 1
\({\text{P}}(B) = {\text{P}}(A \cap B) + {\text{P}}(A’ \cap B)\) M1
\( = {\text{P}}(B|A){\text{P}}(A) + {\text{P}}(B|A’){\text{P}}(A’)\) M1
\( = \frac{1}{3} \times \frac{1}{3} + \frac{1}{6} \times \frac{2}{3} = \frac{2}{9}\) A1
METHOD 2
\({\text{P}}(A \cap B) = {\text{P}}(B|A){\text{P}}(A) \Rightarrow {\text{P}}(A \cap B) = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}\) M1
\({\text{P}}(B) = {\text{P}}(A \cup B) + {\text{P}}(A \cap B) – {\text{P}}(A)\) M1
\({\text{P}}(B) = \frac{4}{9} + \frac{1}{9} – \frac{1}{3} = \frac{2}{9}\) A1
[6 marks]
Examiners report
[N/A]
[N/A]
Question
A bag contains three balls numbered 1, 2 and 3 respectively. Bill selects one of these balls at random and he notes the number on the selected ball. He then tosses that number of fair coins.
Calculate the probability that no head is obtained.
Given that no head is obtained, find the probability that he tossed two coins.
Answer/Explanation
Markscheme
P(no heads from n coins tossed) = \({0.5^n}\) (A1)
P(no head) = \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{8}\) M1
= \(\frac{7}{{24}}\) A1
[3 marks]
\({\text{P(2 | no heads)}} = \frac{{{\text{P(2 coins and no heads)}}}}{{{\text{P(no heads)}}}}\) M1
\( = \frac{{\frac{1}{{12}}}}{{\frac{7}{{24}}}}\) A1
\( = \frac{2}{7}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .
Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
On Saturday, Alfred and Beatrice play 6 different games against each other. In each game, one of the two wins. The probability that Alfred wins any one of these games is \(\frac{2}{3}\).
Show that the probability that Alfred wins exactly 4 of the games is \(\frac{{80}}{{243}}\).
(i) Explain why the total number of possible outcomes for the results of the 6 games is 64.
(ii) By expanding \({(1 + x)^6}\) and choosing a suitable value for x, prove
\[64 = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)\]
(iii) State the meaning of this equality in the context of the 6 games played.
The following day Alfred and Beatrice play the 6 games again. Assume that the probability that Alfred wins any one of these games is still \(\frac{2}{3}\).
(i) Find an expression for the probability Alfred wins 4 games on the first day and 2 on the second day. Give your answer in the form \({\left( {\begin{array}{*{20}{c}}
6 \\
r
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^s}{\left( {\frac{1}{3}} \right)^t}\) where the values of r, s and t are to be found.
(ii) Using your answer to (c) (i) and 6 similar expressions write down the probability that Alfred wins a total of 6 games over the two days as the sum of 7 probabilities.
(iii) Hence prove that \(\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right) = {\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2}\).
Alfred and Beatrice play n games. Let A denote the number of games Alfred wins. The expected value of A can be written as \({\text{E}}(A) = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{a^r}}}{{{b^n}}}\).
(i) Find the values of a and b.
(ii) By differentiating the expansion of \({(1 + x)^n}\), prove that the expected number of games Alfred wins is \(\frac{{2n}}{3}\).
Answer/Explanation
Markscheme
\(B\left( {6,\frac{2}{3}} \right)\) (M1)
\(p(4) = \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right){\left( {\frac{2}{3}} \right)^4}{\left( {\frac{1}{3}} \right)^2}\) A1
\(\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) = 15\) A1
\( = 15 \times \frac{{{2^4}}}{{{3^6}}} = \frac{{80}}{{243}}\) AG
[3 marks]
(i) 2 outcomes for each of the 6 games or \({2^6} = 64\) R1
(ii) \({(1 + x)^6} = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)x + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right){x^2} + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right){x^3} + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right){x^4} + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right){x^5} + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right){x^6}\) A1
Note: Accept \(^n{C_r}\) notation or \(1 + 6x + 15{x^2} + 20{x^3} + 15{x^4} + 6{x^5} + {x^6}\)
setting x = 1 in both sides of the expression R1
Note: Do not award R1 if the right hand side is not in the correct form.
\(64 = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)\) AG
(iii) the total number of outcomes = number of ways Alfred can win no games, plus the number of ways he can win one game etc. R1
[4 marks]
(i) Let \({\text{P}}(x,{\text{ }}y)\) be the probability that Alfred wins x games on the first day and y on the second.
\({\text{P(4, 2)}} = \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^4} \times {\left( {\frac{1}{3}} \right)^2} \times \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^2} \times {\left( {\frac{1}{3}} \right)^4}\) M1A1
\({\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) or \({\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) A1
r = 2 or 4, s = t = 6
(ii) P(Total = 6) =
P(0, 6) + P(1, 5) + P(2, 4) + P(3, 3) + P(4, 2) + P(5, 1) + P(6, 0) (M1)
\( = {\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6} + … + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) A2
\( = \frac{{{2^6}}}{{{3^{12}}}}\left( {{{\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)}^2}} \right)\)
Note: Accept any valid sum of 7 probabilities.
(iii) use of \(\left( {\begin{array}{*{20}{c}}
6 \\
i
\end{array}} \right) = \left( {\begin{array}{*{20}{l}}
6 \\
{6 – i}
\end{array}} \right)\) (M1)
(can be used either here or in (c)(ii))
P(wins 6 out of 12) \( = \left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^6} \times {\left( {\frac{1}{3}} \right)^6} = \frac{{{2^6}}}{{{3^{12}}}}\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) A1
\( = \frac{{{2^6}}}{{{3^{12}}}}\left( {{{\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)}^2}} \right) = \frac{{{2^6}}}{{{3^{12}}}}\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) A1
therefore \({\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) AG
[9 marks]
(i) \({\text{E}}(A) = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} {\left( {\frac{2}{3}} \right)^r}{\left( {\frac{1}{3}} \right)^{n – r}} = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{2^r}}}{{{3^n}}}\)
(a = 2, b = 3) M1A1
Note: M0A0 for a = 2, b = 3 without any method.
(ii) \(n{(1 + x)^{n – 1}} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r{x^{r – 1}}\) A1A1
(sigma notation not necessary)
(if sigma notation used also allow lower limit to be r = 0)
let x = 2 M1
\(n{3^{n – 1}} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r{2^{r – 1}}\)
multiply by 2 and divide by \({3^n}\) (M1)
\(\frac{{2n}}{3} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r\frac{{{2^r}}}{{{3^n}}}\left( { = \sum\limits_{r = 0}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{2^r}}}{{{3^n}}}} \right)\) AG
[6 marks]
Examiners report
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(a) Candidates need to be aware how to work out binomial coefficients without a calculator
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(b) (ii) A surprising number of candidates chose to work out the values of all the binomial coefficients (or use Pascal’s triangle) to make a total of 64 rather than simply putting 1 into the left hand side of the expression.
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(d) This was poorly done. Candidates were not able to manipulate expressions given using sigma notation.
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.2\) and \({\text{P}}(B) = 0.5\).
Determine the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Determine the range of possible values of \({\text{P}}\left( {A|B} \right)\).
Answer/Explanation
Markscheme
(i) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5\)
\( = 0.7\) A1
(ii) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5 – 0.1\)
\( = 0.6\) A1
[4 marks]
\({\text{P}}\left( {A|B} \right) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
\({\text{P}}\left( {A|B} \right)\) is a maximum when \({\text{P}}(A \cap B) = {\text{P}}(A)\)
\({\text{P}}\left( {A|B} \right)\) is a minimum when \({\text{P}}(A \cap B) = 0\)
\(0 \le {\text{P}}\left( {A|B} \right) \le 0.4\) A1A1A1
Note: A1 for each endpoint and A1 for the correct inequalities.
[3 marks]
Total [7 marks]
Examiners report
This part was generally well done.
Disappointingly, many candidates did not seem to understand the meaning of the word ‘range’ in this context.
Question
A football team, Melchester Rovers are playing a tournament of five matches.
The probabilities that they win, draw or lose a match are \(\frac{1}{2}\), \(\frac{1}{6}\) and \(\frac{1}{3}\) respectively.
These probabilities remain constant; the result of a match is independent of the results of other matches. At the end of the tournament their coach Roy loses his job if they lose three consecutive matches, otherwise he does not lose his job. Find the probability that Roy loses his job.
Answer/Explanation
Markscheme
METHOD 1
to have \(3\) consecutive losses there must be exactly \(5\), \(4\) or \(3\) losses
the probability of exactly \(5\) losses (must be \(3\) consecutive) is \({\left( {\frac{1}{3}} \right)^5}\) A1
the probability of exactly \(4\) losses (with \(3\) consecutive) is \(4{\left( {\frac{1}{3}} \right)^4}\left( {\frac{2}{3}} \right)\) A1A1
Note: First A1 is for the factor \(4\) and second A1 for the other \(2\) factors.
the probability of exactly \(3\) losses (with \(3\) consecutive) is \(3{\left( {\frac{1}{3}} \right)^3}{\left( {\frac{2}{3}} \right)^2}\) A1A1
Note: First A1 is for the factor \(3\) and second A1 for the other \(2\) factors.
(Since the events are mutually exclusive)
the total probability is \(\frac{{1 + 8 + 12}}{{{3^5}}} = \frac{{21}}{{243}}\;\;\;\left( { = \frac{7}{{81}}} \right)\) A1
[6 marks]
METHOD 2
Roy loses his job if
A – first \(3\) games are all lost (so the last \(2\) games can be any result)
B – first \(3\) games are not all lost, but middle \(3\) games are all lost (so the first game is not a loss and the last game can be any result)
or C – first \(3\) games are not all lost, middle \(3\) games are not all lost but last \(3\) games are all lost, (so the first game can be any result but the second game is not a loss)
for A \({4^{{\text{th}}}}\) & \({5^{{\text{th}}}}\) games can be anything
\({\text{P}}(A) = {\left( {\frac{1}{3}} \right)^3} = \frac{1}{{27}}\) A1
for B \({1^{{\text{st}}}}\) game not a loss & \({5^{{\text{th}}}}\) game can be anything (R1)
\({\text{P}}(B) = \frac{2}{3} \times {\left( {\frac{1}{3}} \right)^3} = \frac{2}{{81}}\) A1
for C \({1^{{\text{st}}}}\) game anything, \({2^{{\text{nd}}}}\) game not a loss (R1)
\({\text{P}}(C) = 1 \times \frac{2}{3} \times {\left( {\frac{1}{3}} \right)^3} = \frac{2}{{81}}\) A1
(Since the events are mutually exclusive)
total probability is \(\frac{1}{{27}} + \frac{2}{{81}} + \frac{2}{{81}} = \frac{7}{{81}}\) A1
Note: In both methods all the A marks are independent.
Note: If the candidate misunderstands the question and thinks that it is asking for exactly \(3\) losses award A1 A1 and A1 for an answer of \(\frac{{12}}{{243}}\) as in the last lines of Method 1.
[6 marks]
Total [6 marks]
Examiners report
If a script has lots of numbers with the wrong final answer and no explanation of method it is not going to gain many marks. Working has to be explained. The counting strategy needs to be decided on first. Some candidates misunderstood the context and tried to calculate exactly \(3\) consecutive losses. Not putting a non-loss as \(\frac{2}{3}\) caused unnecessary work.
Question
\(A\) and \(B\) are two events such that \({\text{P}}(A) = 0.25,{\text{ P}}(B) = 0.6\) and \({\text{P}}(A \cup B) = 0.7\).
Find \({\text{P}}(A \cap B)\).
Determine whether events \(A\) and \(B\) are independent.
Answer/Explanation
Markscheme
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\({\text{P}}(A \cap B) = 0.25 + 0.6 = 0.7\) M1
\( = 0.15\) A1
[2 marks]
EITHER
\({\text{P}}(A){\text{P}}(B)( = 0.25 \times 0.6) = 0.15\) A1
\( = {\text{P}}(A \cap B)\) so independent R1
OR
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}} = \frac{{0.15}}{{0.6}} = 0.25\) A1
\( = {\text{P}}(A)\) so independent R1
Note: Allow follow through for incorrect answer to (a) that will result in events being dependent in (b).
[2 marks]
Total [4 marks]
Examiners report
[N/A]
[N/A]
