Question
Consider the function f defined by f (x) = ln (x2 – 16) for x > 4 .
The following diagram shows part of the graph of f which crosses the x-axis at point A, with
coordinates ( a , 0 ). The line L is the tangent to the graph of f at the point B.
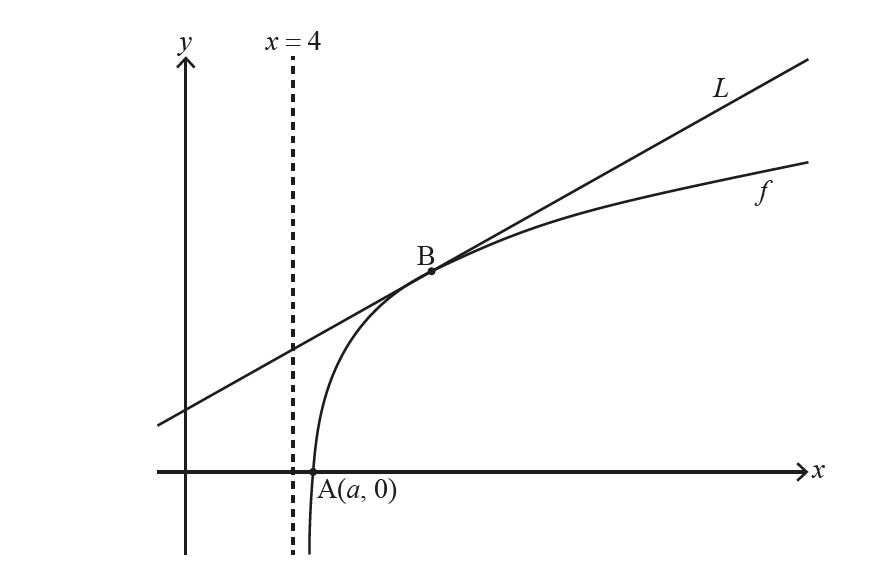
(a) Find the exact value of a . [3]
(b) Given that the gradient of L is \(\frac{1}{3}\) , find the x-coordinate of B. [6]
▶️Answer/Explanation
Ans:
(a) When f(x)=0, we have
ln(x2−16)=0
x2−16=1
x=±√17
However, since x>4, we have x=√17
(b) Differentiating f(x) with respect to x, we have f′(x)= \(\frac{2x}{x^2-16}\)
At B, f′(x)=\(\frac{1}{3}\) , i.e., we have
x2−16=6x
x2−6x−16=0
(x+2)(x−8)=0.
Thus, x=−2 (reject) or x=8.
Question
Let \(\{ {u_n}\} ,{\text{ }}n \in {\mathbb{Z}^ + }\), be an arithmetic sequence with first term equal to \(a\) and common difference of \(d\), where \(d \ne 0\). Let another sequence \(\{ {v_n}\} ,{\text{ }}n \in {\mathbb{Z}^ + }\), be defined by \({v_n} = {2^{{u_n}}}\).
a.(i) Show that \(\frac{{{v_{n + 1}}}}{{{v_n}}}\) is a constant.
(ii) Write down the first term of the sequence \(\{ {v_n}\} \).
(iii) Write down a formula for \({v_n}\) in terms of \(a\), \(d\) and \(n\).[4]
b.Let \({S_n}\) be the sum of the first \(n\) terms of the sequence \(\{ {v_n}\} \).
(i) Find \({S_n}\), in terms of \(a\), \(d\) and \(n\).
(ii) Find the values of \(d\) for which \(\sum\limits_{i = 1}^\infty {{v_i}} \) exists.
You are now told that \(\sum\limits_{i = 1}^\infty {{v_i}} \) does exist and is denoted by \({S_\infty }\).
(iii) Write down \({S_\infty }\) in terms of \(a\) and \(d\) .
(iv) Given that \({S_\infty } = {2^{a + 1}}\) find the value of \(d\) .[8]
c.Let \(\{ {w_n}\} ,{\text{ }}n \in {\mathbb{Z}^ + }\), be a geometric sequence with first term equal to \(p\) and common ratio \(q\), where \(p\) and \(q\) are both greater than zero. Let another sequence \(\{ {z_n}\} \) be defined by \({z_n} = \ln {w_n}\).
Find \(\sum\limits_{i = 1}^n {{z_i}} \) giving your answer in the form \(\ln k\) with \(k\) in terms of \(n\), \(p\) and \(q\).[6]
▶️Answer/Explanation
Markscheme
(i) METHOD 1
\(\frac{{{v_{n + 1}}}}{{{v_n}}} = \frac{{{2^{{u_{n + 1}}}}}}{{{2^{{u_n}}}}}\) M1
\( = {2^{{u_{n + 1}} – {u_n}}} = {2^d}\) A1
METHOD 2
\(\frac{{{v_{n + 1}}}}{{{v_n}}} = \frac{{{2^{a + nd}}}}{{{2^{a + (n – 1)d}}}}\) M1
\( = {2^d}\) A1
(ii) \( = {2^a}\) A1
Note: Accept \( = {2^{{u_1}}}\).
(iii) EITHER
\({v_n}\) is a GP with first term \({2^a}\) and common ratio \({2^d}\)
\({v_n} = {2^a}{({2^d})^{(n – 1)}}\)
OR
\({u_n} = a + (n – 1)d\) as it is an AP
THEN
\({v_n} = {2^a}^{ + (n – 1)d}\) A1
[4 marks]
(i) \({S_n} = \frac{{{2^a}\left( {{{({2^d})}^n} – 1} \right)}}{{{2^d} – 1}} = \frac{{{2^a}({2^{dn}} – 1)}}{{{2^d} – 1}}\) M1A1
Note: Accept either expression.
(ii) for sum to infinity to exist need \( – 1 < {2^d} < 1\) R1
\( \Rightarrow \log {2^d} < 0 \Rightarrow d\log 2 < 0 \Rightarrow d < 0\) (M1)A1
Note: Also allow graph of \({2^d}\).
(iii) \({S_\infty } = \frac{{{2^a}}}{{1 – {2^d}}}\) A1
(iv) \(\frac{{{2^a}}}{{1 – {2^d}}} = {2^{a + 1}} \Rightarrow \frac{1}{{1 – {2^d}}} = 2\) M1
\( \Rightarrow 1 = 2 – {2^{d + 1}} \Rightarrow {2^{d + 1}} = 1\)
\( \Rightarrow d = – 1\) A1
[8 marks]
METHOD 1
\({w_n} = p{q^{n – 1}},{\text{ }}{z_n} = \ln p{q^{n – 1}}\) (A1)
\({z_n} = \ln p + (n – 1)\ln q\) M1A1
\({z_{n + 1}} – {z_n} = (\ln p + n\ln q) – (\ln p + (n – 1)\ln q) = \ln q\)
which is a constant so this is an AP
(with first term \(\ln p\) and common difference \(\ln q\))
\(\sum\limits_{i = 1}^n {{z_i} = \frac{n}{2}\left( {2\ln p + (n – 1)\ln q} \right)} \) M1
\( = n\left( {\ln p + \ln {q^{\left( {\frac{{n – 1}}{2}} \right)}}} \right) = n\ln \left( {p{q^{\left( {\frac{{n – 1}}{2}} \right)}}} \right)\) (M1)
\( = \ln \left( {{p^n}{q^{\frac{{n(n – 1)}}{2}}}} \right)\) A1
METHOD 2
\(\sum\limits_{i = 1}^n {{z_i} = \ln p + \ln pq + \ln p{q^2} + \ldots + \ln p{q^{n – 1}}} \) (M1)A1
\( = \ln \left( {{p^n}{q^{\left( {1 + 2 + 3 + \ldots + (n – 1)} \right)}}} \right)\) (M1)A1
\( = \ln \left( {{p^n}{q^{\frac{{n(n – 1)}}{2}}}} \right)\) (M1)A1
[6 marks]
Total [18 marks]
Question
Find integer values of \(m\) and \(n\) for which
\[m – n{\log _3}2 = 10{\log _9}6\]
▶️Answer/Explanation
Markscheme
METHOD 1
\(m – n{\log _3}2 = 10{\log _9}6\)
\(m – n{\log _3}2 = 5{\log _3}6\) M1
\(m = {\log _3}\left( {{6^5}{2^n}} \right)\) (M1)
\({3^m}{2^{ – n}} = {6^5} = {3^5} \times {2^5}\) (M1)
\(m = 5,{\text{ }}n = – 5\) A1
Note: First M1 is for any correct change of base, second M1 for writing as a single logarithm, third M1 is for writing 6 as \(2 \times 3\).
METHOD 2
\(m – n{\log _3}2 = 10{\log _9}6\)
\(m – n{\log _3}2 = 5{\log _3}6\) M1
\(m – n{\log _3}2 = 5{\log _3}3 + 5{\log _3}2\) (M1)
\(m – n{\log _3}2 = 5 + 5{\log _3}2\) (M1)
\(m = 5,{\text{ }}n = – 5\) A1
Note: First M1 is for any correct change of base, second M1 for writing 6 as \(2 \times 3\) and third M1 is for forming an expression without \({\log _3}3\).
[4 marks]
Question
Solve the equation \({4^x} + {2^{x + 2}} = 3\).
▶️Answer/Explanation
Markscheme
attempt to form a quadratic in \({2^x}\) M1
\({({2^x})^2} + 4 \bullet {2^x} – 3 = 0\) A1
\({2^x} = \frac{{ – 4 \pm \sqrt {16 + 12} }}{2}{\text{ }}\left( { = – 2 \pm \sqrt 7 } \right)\) M1
\({2^x} = – 2 + \sqrt 7 {\text{ }}\left( {{\text{as }} – 2 – \sqrt 7 < 0} \right)\) R1
\(x = {\log _2}\left( { – 2 + \sqrt 7 } \right){\text{ }}\left( {x = \frac{{\ln \left( { – 2 + \sqrt 7 } \right)}}{{\ln 2}}} \right)\) A1
Note: Award R0 A1 if final answer is \(x = {\log _2}\left( { – 2 + \sqrt 7 } \right)\).
[5 marks]
