Question
Solve the equation \(2 – {\log _3}(x + 7) = {\log _{\tfrac{1}{3}}}2x\) .
▶️Answer/Explanation
Markscheme
\({\log _3}\left( {\frac{9}{{x + 7}}} \right) = {\log _3}\frac{1}{{2x}}\) M1M1A1
Note: Award M1 for changing to single base, M1 for incorporating the 2 into a log and A1 for a correct equation with maximum one log expression each side.
\(x + 7 = 18x\) M1
\(x = \frac{7}{{17}}\) A1
[5 marks]
Question
Consider \(a = {\log _2}3 \times {\log _3}4 \times {\log _4}5 \times \ldots \times {\log _{31}}32\). Given that \(a \in \mathbb{Z}\), find the value of a.
▶️Answer/Explanation
Markscheme
\(\frac{{\log 3}}{{\log 2}} \times \frac{{\log 4}}{{\log 3}} \times \ldots \times \frac{{\log 32}}{{\log 31}}\) M1A1
\( = \frac{{\log 32}}{{\log 2}}\) A1
\( = \frac{{5\log 2}}{{\log 2}}\) (M1)
\( = 5\) A1
hence \(a = 5\)
Note: Accept the above if done in a specific base eg \({\log _2}x\).
[5 marks]
Question
Let \(f(x) = \ln x\) . The graph of f is transformed into the graph of the function g by a translation of \(\left( {\begin{array}{*{20}{c}}
3 \\
{ – 2}
\end{array}} \right)\), followed by a reflection in the x-axis. Find an expression for \(g(x)\), giving your answer as a single logarithm.
▶️Answer/Explanation
Markscheme
\(h(x) = f(x – 3) – 2 = \ln (x – 3) – 2\) (M1)(A1)
\(g(x) = -h(x) = 2 – \ln (x – 3)\) M1
Note: Award M1 only if it is clear the effect of the reflection in the x-axis:
the expression is correct OR
there is a change of signs of the previous expression OR
there’s a graph or an explanation making it explicit
\( = \ln {{\text{e}}^2} – \ln (x – 3)\) M1
\( = \ln \left( {\frac{{{{\text{e}}^2}}}{{x – 3}}} \right)\) A1
[5 marks]
Examiners report
This question was well attempted but many candidates could have scored better had they written down all the steps to obtain the final expression. In some cases, as the final expression was incorrect and the middle steps were missing, candidates scored just 1 mark. That could be a consequence of a small mistake, but the lack of working prevented them from scoring at least all method marks. Some candidates performed the transformations well but were not able to use logarithms properties to transform the answer and give it as a single logarithm.
Question
It has been suggested that in rowing competitions the time, \(T\) seconds taken to complete a 2000 m race can be modelled by an equation of the form \(T = a{N^b}\), where \(N\) is the number of rowers in the boat and \(a\) and \(b\) are constants for rowers of a similar standard.
To test this model the times for the finalists in all the 2000 m men’s races at a recent Olympic games were recorded and the mean calculated.
The results are shown in the following table for \(N = 1\) and \(N = 2\).
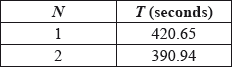
It is now given that the mean time in the final for boats with 8 rowers was 342.08 seconds.
a.Use these results to find estimates for the value of \(a\) and the value of \(b\). Give your answers to five significant figures.[4]
b.Use this model to estimate the mean time for the finalists in an Olympic race for boats with 8 rowers. Give your answer correct to two decimal places.[1]
c.Calculate the error in your estimate as a percentage of the actual value.[1]
d.Comment on the likely validity of the model as \(N\) increases beyond 8.[2]
▶️Answer/Explanation
Markscheme
\(a = 420.65\) A1
\(390.94 = a \times {2^b}\) M1
\({2^b} = \frac{{390.94}}{{420.65}} = 0.929 \ldots \) A1
\(b = – 0.10567\) A1
[4 marks]
\(N = 8\,\,\,T = 337.67\) A1
Note: Accept 5sf answers between 337.44 and 337.67.
[1 mark]
\(N = 8\) Percentage error 1.29% A1
Note: Accept negative values of the above.
[1 mark]
likely not to be a good fit for larger values of \(N\) R1
likely to be quite a good fit for values close to 8 R1
[2 marks]
Examiners report
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations. Part (d) caused more difficulties as candidates frequently had insufficient analysis to gain the two marks.
Question
Solve the simultaneous equations
\[\ln \frac{y}{x} = 2\]
\[\ln {x^2} + \ln {y^3} = 7.\]
▶️Answer/Explanation
Markscheme
METHOD 1
\(\ln \frac{y}{x} = 2 \Rightarrow \ln x + \ln y = 2\) A1
\(\ln {x^2} + \ln {y^3} = 7 \Rightarrow 2\ln x + 3\ln y = 7\) (M1)A1
attempting to solve for \(x\) and \(y\) \(\left( {{\text{to obtain }}\ln x = \frac{1}{5}{\text{ and }}\ln y = \frac{{11}}{5}} \right)\) (M1)
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
METHOD 2
\(\ln \frac{y}{x} = 2 \Rightarrow y = {{\text{e}}^2}x\) A1
\(\ln {x^2} + \ln {{\text{e}}^6}{x^3} = 7\) (M1)A1
attempting to solve for \(x\) (M1)
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
METHOD 3
\(\ln \frac{y}{x} = 2 \Rightarrow y = {{\text{e}}^2}x\) A1
\(\ln {x^2} + \ln {y^3} = 7 \Rightarrow \ln ({x^2}{y^3}) = 7\) A1
\({x^2}{y^3} = {{\text{e}}^7}\) (M1)
substituting \(y = {e^2}x\) into \({x^2}{y^3} = {{\text{e}}^7}\) (to obtain \({{\text{e}}^6}{x^5} = {{\text{e}}^7}\)) M1
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
[6 marks]
Examiners report
Reasonably well done. Candidates who did not obtain the correct solution generally made an error when attempting to apply logarithmic or exponential laws and hence made erroneous substitutions.
