Question
The points P(−1, 2, − 3), Q(−2, 1, 0), R(0, 5, 1) and S form a parallelogram, where S is diagonally opposite Q.
a.Find the coordinates of S.[2]
b.The vector product \(\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
m
\end{array}} \right)\). Find the value of m .[2]
c.Hence calculate the area of parallelogram PQRS.[2]
d.Find the Cartesian equation of the plane, \({\prod _1}\) , containing the parallelogram PQRS.[3]
f.Hence find the point on the plane that is closest to the origin.[3]
g.A second plane, \({\prod _2}\) , has equation x − 2y + z = 3. Calculate the angle between the two planes.[4]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
3
\end{array}} \right)\) , \(\overrightarrow {{\text{SR}}} = \left( {\begin{array}{*{20}{c}}
{0 – x} \\
{5 – y} \\
{1 – z}
\end{array}} \right)\) (M1)
point S = (1, 6, −2) A1
[2 marks]
\(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
3
\end{array}} \right)\)\(\overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
2 \\
4 \\
1
\end{array}} \right)\) A1
\(\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
{ – 2}
\end{array}} \right)\)
m = −2 A1
[2 marks]
area of parallelogram PQRS \( = \left| {\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} } \right| = \sqrt {{{( – 13)}^2} + {7^2} + {{( – 2)}^2}} \) M1
\( = \sqrt {222} = 14.9\) A1
[2 marks]
equation of plane is −13x + 7y − 2z = d M1A1
substituting any of the points given gives d = 33
−13x + 7y − 2z = 33 A1
[3 marks]
equation of line is \(\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
0 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
{ – 2}
\end{array}} \right)\) A1
Note: To get the A1 must have \(\boldsymbol{r} =\) or equivalent.
[1 mark]
\(169\lambda + 49\lambda + 4\lambda = 33\) M1
\(\lambda = \frac{{33}}{{222}}{\text{ }}( = 0.149…)\) A1
closest point is \(\left( { – \frac{{143}}{{74}},\frac{{77}}{{74}}, – \frac{{11}}{{37}}} \right){\text{ }}\left( { = ( – 1.93,{\text{ 1.04, – 0.297)}}} \right)\) A1
[3 marks]
angle between planes is the same as the angle between the normals (R1)
\(\cos \theta = \frac{{ – 13 \times 1 + 7 \times – 2 – 2 \times 1}}{{\sqrt {222} \times \sqrt 6 }}\) M1A1
\(\theta = 143^\circ \) (accept \(\theta = 37.4^\circ \) or 2.49 radians or 0.652 radians) A1
[4 marks]
Question
Two submarines A and B have their routes planned so that their positions at time t hours, 0 ≤ t < 20 , would be defined by the position vectors rA
\(\left( \begin{gathered}
\,2 \hfill \\
\,4 \hfill \\
– 1 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
– 1 \hfill \\
\,1 \hfill \\
– 0.15 \hfill \\
\end{gathered} \right)\)
and rB \( = \left( \begin{gathered}
\,0 \hfill \\
\,3.2 \hfill \\
– 2 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
– 0.5 \hfill \\
\,1.2 \hfill \\
\,0.1 \hfill \\
\end{gathered} \right)\)
relative to a fixed point on the surface of the ocean (all lengths are in kilometres).
To avoid the collision submarine B adjusts its velocity so that its position vector is now given by
rB \( = \left( \begin{gathered}
\,0 \hfill \\
\,3.2 \hfill \\
– 2 \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
– 0.45 \hfill \\
\,1.08 \hfill \\
\,0.09 \hfill \\
\end{gathered} \right)\).
a.Show that the two submarines would collide at a point P and write down the coordinates of P.[4]
b.i.Show that submarine B travels in the same direction as originally planned.[1]
b.ii.Find the value of t when submarine B passes through P.[2]
c.i.Find an expression for the distance between the two submarines in terms of t.[5]
c.ii.Find the value of t when the two submarines are closest together.[2]
c.iii.Find the distance between the two submarines at this time.[1]
▶️Answer/Explanation
Markscheme
rA = rB (M1)
2 − t = − 0.5t ⇒ t = 4 A1
checking t = 4 satisfies 4 + t = 3.2 + 1.2t and − 1 − 0.15t = − 2 + 0.1t R1
P(−2, 8, −1.6) A1
Note: Do not award final A1 if answer given as column vector.
[4 marks]
\(0.9 \times \left( \begin{gathered}
– 0.5 \hfill \\
\,1.2 \hfill \\
\,0.1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
– 0.45 \hfill \\
\,1.08 \hfill \\
\,0.09 \hfill \\
\end{gathered} \right)\) A1
Note: Accept use of cross product equalling zero.
hence in the same direction AG
[1 mark]
\(\left( \begin{gathered}
\, – 0.45t \hfill \\
3.2 + 1.08t \hfill \\
– 2 + 0.09t \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
– 2 \hfill \\
\,8 \hfill \\
– 1.6 \hfill \\
\end{gathered} \right)\) M1
Note: The M1 can be awarded for any one of the resultant equations.
\( \Rightarrow t = \frac{{40}}{9} = 4.44 \ldots \) A1
[2 marks]
rA − rB = \(\left( \begin{gathered}
\,2 – t \hfill \\
\,4 + t \hfill \\
– 1 – 0.15t \hfill \\
\end{gathered} \right) – \left( \begin{gathered}
\, – 0.45t \hfill \\
3.2 + 1.08t \hfill \\
– 2 + 0.09t \hfill \\
\end{gathered} \right)\) (M1)(A1)
\( = \left( \begin{gathered}
\,2 – 0.55t \hfill \\
\,0.8 – 0.08t \hfill \\
1 – 0.24t \hfill \\
\end{gathered} \right)\) (A1)
Note: Accept rA − rB.
distance \(D = \sqrt {{{\left( {2 – 0.55t} \right)}^2} + {{\left( {0.8 – 0.08t} \right)}^2} + {{\left( {1 – 0.24t} \right)}^2}} \) M1A1
\(\left( { = \sqrt {8.64 – 2.688t + 0.317{t^2}} } \right)\)
[5 marks]
minimum when \(\frac{{{\text{d}}D}}{{{\text{d}}t}} = 0\) (M1)
t = 3.83 A1
[2 marks]
0.511 (km) A1
[1 mark]
Question
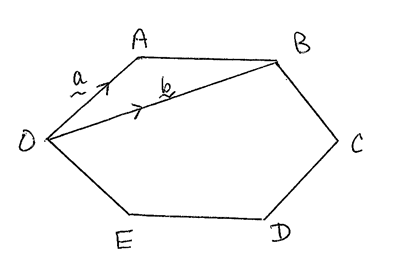
OABCDE is a regular hexagon and a , b denote respectively the position vectors of A, B with respect to O.
a.Show that OC = 2AB .[2]
b.Find the position vectors of C, D and E in terms of a and b .[7]
▶️Answer/Explanation
Markscheme
\({\text{OC}} = {\text{AB}} + {\text{OA}}\cos 60 + {\text{BC}}\cos 60\) M1
\( = {\text{AB}} + {\text{AB}} \times \frac{1}{2} + {\text{AB}} \times \frac{1}{2}\) A1
\( = 2{\text{AB}}\) AG
[2 marks]
\(\overrightarrow {{\text{OC}}} = 2\overrightarrow {{\text{AB}}} = \)2(b – a) M1A1
\(\overrightarrow {{\text{OD}}} = \overrightarrow {{\text{OC}}} + \overrightarrow {{\text{CD}}} \) M1
\( = \overrightarrow {{\text{OC}}} + \overrightarrow {{\text{AO}}} \) A1
= 2b – 2a – a = 2b – 3a A1
\(\overrightarrow {{\text{OE}}} = \overrightarrow {{\text{BC}}} \) M1
= 2b – 2a – b = b – 2a A1
[7 marks]
