Question
All living plants contain an isotope of carbon called carbon-14. When a plant dies, the isotope decays so that the amount of carbon-14 present in the remains of the plant decreases. The time since the death of a plant can be determined by measuring the amount of carbon-14 still present in the remains.
The amount, A , of carbon-14 present in a plant t years after its death can be modelled by A = A0e-kt where t ≥ 0 and A0 , k are positive constants.
At the time of death, a plant is defined to have 100 units of carbon-14.
(a) Show that A0 = 100 . [1]
The time taken for half the original amount of carbon-14 to decay is known to be 5730 years.
(b) Show that \(k=\frac{ln 2}{5730}\) [3]
(c) Find, correct to the nearest 10 years, the time taken after the plant’s death for 25 % of the carbon-14 to decay. [3]
Answer/Explanation
Ans:
(a) When $t=0$, $A=100$, i.e., we have $$\begin{eqnarray} 100 = A_0\text{e}^{-k\left(0\right)} \nonumber \\ A_0 = 100. \end{eqnarray}$$ (b) Let half-life be $t=5730$, then $$\begin{eqnarray} \frac{1}{2} = \text{e}^{-k\left(5730\right)} \nonumber \\ -\ln 2 = -k\left(5730\right) \nonumber \\ k = \frac{\ln 2}{5730}. \end{eqnarray}$$ (c) When $25%$ of carbon-14 has decayed, we are left with $A=75$. Thus, from the graphing calculator, solving $75=100\text{e}^{-\frac{\ln 2}{5730}t}$, we have $t\approx 2380\text{ years}$.
Question
Solve the following system of equations.
\[{\log _{x + 1}}y = 2\]\[{\log _{y + 1}}x = \frac{1}{4}\]
Answer/Explanation
Markscheme
\({\log _{x + 1}}y = 2\)
\({\log _{y + 1}}x = \frac{1}{4}\)
so \({\left( {x + 1} \right)^2} = y\) A1
\({\left( {y + 1} \right)^{\frac{1}{4}}} = x\) A1
EITHER
\({x^4} – 1 = {\left( {x + 1} \right)^2}\) M1
\(x = – 1\), not possible R1
\(x = 1.70\), \(y = 7.27\) A1A1
OR
1
\({\left( {{x^2} + 2x + 2} \right)^{\frac{1}{4}}} – x = 0\) M1
attempt to solve or graph of LHS M1
\(x =1.70\), \(y = 7.27\) A1A1
[6 marks]
Question
It has been suggested that in rowing competitions the time, \(T\) seconds taken to complete a 2000 m race can be modelled by an equation of the form \(T = a{N^b}\), where \(N\) is the number of rowers in the boat and \(a\) and \(b\) are constants for rowers of a similar standard.
To test this model the times for the finalists in all the 2000 m men’s races at a recent Olympic games were recorded and the mean calculated.
The results are shown in the following table for \(N = 1\) and \(N = 2\).
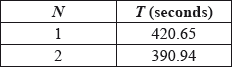
It is now given that the mean time in the final for boats with 8 rowers was 342.08 seconds.
Use these results to find estimates for the value of \(a\) and the value of \(b\). Give your answers to five significant figures.[4]
Use this model to estimate the mean time for the finalists in an Olympic race for boats with 8 rowers. Give your answer correct to two decimal places.[1]
Calculate the error in your estimate as a percentage of the actual value.[1]
Comment on the likely validity of the model as \(N\) increases beyond 8.[2]
Answer/Explanation
Markscheme
\(a = 420.65\) A1
\(390.94 = a \times {2^b}\) M1
\({2^b} = \frac{{390.94}}{{420.65}} = 0.929 \ldots \) A1
\(b = – 0.10567\) A1
[4 marks]
\(N = 8\,\,\,T = 337.67\) A1
Note: Accept 5sf answers between 337.44 and 337.67.
[1 mark]
\(N = 8\) Percentage error 1.29% A1
Note: Accept negative values of the above.
[1 mark]
likely not to be a good fit for larger values of \(N\) R1
likely to be quite a good fit for values close to 8 R1
[2 marks]
Question
Solve the simultaneous equations
\[\ln \frac{y}{x} = 2\]
\[\ln {x^2} + \ln {y^3} = 7.\]
Answer/Explanation
Markscheme
METHOD 1
\(\ln \frac{y}{x} = 2 \Rightarrow \ln x + \ln y = 2\) A1
\(\ln {x^2} + \ln {y^3} = 7 \Rightarrow 2\ln x + 3\ln y = 7\) (M1)A1
attempting to solve for \(x\) and \(y\) \(\left( {{\text{to obtain }}\ln x = \frac{1}{5}{\text{ and }}\ln y = \frac{{11}}{5}} \right)\) (M1)
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
METHOD 2
\(\ln \frac{y}{x} = 2 \Rightarrow y = {{\text{e}}^2}x\) A1
\(\ln {x^2} + \ln {{\text{e}}^6}{x^3} = 7\) (M1)A1
attempting to solve for \(x\) (M1)
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
METHOD 3
\(\ln \frac{y}{x} = 2 \Rightarrow y = {{\text{e}}^2}x\) A1
\(\ln {x^2} + \ln {y^3} = 7 \Rightarrow \ln ({x^2}{y^3}) = 7\) A1
\({x^2}{y^3} = {{\text{e}}^7}\) (M1)
substituting \(y = {e^2}x\) into \({x^2}{y^3} = {{\text{e}}^7}\) (to obtain \({{\text{e}}^6}{x^5} = {{\text{e}}^7}\)) M1
\(x = {{\text{e}}^{\frac{1}{5}}}{\text{ }}( = 1.22)\) A1
\(y = {{\text{e}}^{\frac{{11}}{5}}}{\text{ }}( = 9.03)\) A1
[6 marks]
