Question
Let G be a simple, connected, planar graph.
(a) (i) Show that Euler’s relation \(f – e + v = 2\) is valid for a spanning tree of G.
(ii) By considering the effect of adding an edge on the values of f, e and v show that Euler’s relation remains true.
(b) Show that K5 is not planar.
▶️Answer/Explanation
Markscheme
(a) (i) A spanning tree with v vertices and (v −1) edges where f = 1 A1A1
f − e + v =1 − (v − 1) + v = 2 M1
So the formula is true for the tree AG
(ii) Adding one edge connects two different vertices, and hence an extra face is created M1R1
This leaves v unchanged but increases both e and f by 1 leaving f − e + v unchanged. Hence f − e + v = 2 . R1R1
[7 marks]
(b) Using \(e \leqslant 3v – 6\) , M1
for \({K_5},{\text{ }}v = 5\) and \(e = \left( {\begin{array}{*{20}{c}}
5 \\
2
\end{array}} \right) = 10\) A1A1
but 3v − 6 = 3(5) − 6 = 9 A1
9 is not greater or equal to 10 so \({K_5}\) is not planar R1
[5 marks]
Total [12 marks]
Examiners report
Part (a)(i) was done successfully but many students did not read part(ii) carefully. It said ‘adding an edge’ nothing else. Many candidates assumed it was necessary to add a vertex when this was not the case.
Part (b) was not found to be beyond many candidates if they used the inequality \(e \leqslant 3v – 6\)
Question
(a) Show that, for a connected planar graph,
\[v + f – e = 2.\]
(b) Assuming that \(v \geqslant 3\), explain why, for a simple connected planar graph, \(3f \leqslant 2e\) and hence deduce that \(e \leqslant 3v – 6\).
(c) The graph G and its complement \({G’}\) are simple connected graphs, each having 12 vertices. Show that \({G}\) and \({G’}\) cannot both be planar.
▶️Answer/Explanation
Markscheme
(a) start with a graph consisting of just a single vertex M1
for this graph, v = 1, f = 1 and e = 0, the relation is satisfied A1
Note: Allow solutions that begin with 2 vertices and 1 edge.
to extend the graph you either join an existing vertex to another existing vertex which increases e by 1 and f by 1 so that v + f – e remains equal to 2 M1A1
or add a new vertex and a corresponding edge which increases e by 1 and v by 1 so that v + f – e remains equal to 2 M1A1
therefore, however we build up the graph, the relation remains valid R1
[7 marks]
(b) since every face is bounded by at least 3 edges, the result follows by counting up the edges around each face R1
the factor 2 follows from the fact that every edge bounds (at most) 2 faces R1
hence \(3f \leqslant 2e\) AG
from the Euler relation, \(3f = 6 + 3e – 3v\) M1
substitute in the inequality, \(6 + 3e – 3v \leqslant 2e\) A1
hence \(e \leqslant 3v – 6\) AG
[4 marks]
(c) let G have e edges M1
since G and \({G’}\) have a total of \(\left( {\begin{array}{*{20}{c}}
{12} \\
2
\end{array}} \right) = 66\) edges A1
it follows that \({G’}\) has 66 – e edges A1
for planarity we require
\(e \leqslant 3 \times 12 – 6 = 30\) M1A1
and \(66 – e \leqslant 30 \Rightarrow e \geqslant 36\) A1
these two inequalities cannot both be met indicating that both graphs cannot be planar R1
[7 marks]
Total [18 marks]
Examiners report
Parts (a) and (b) were found difficult by many candidates with explanations often inadequate. In (c), candidates who realised that the union of a graph with its complement results in a complete graph were often successful.
Question
(i) A graph is simple, planar and connected. Write down the inequality connecting v and e, and give the condition on v for this inequality to hold.
(ii) Sketch a simple, connected, planar graph with v = 2 where the inequality from part (b)(i) is not true.
(iii) Sketch a simple, connected, planar graph with v =1 where the inequality from part (b)(i) is not true.
(iv) Given a connected, planar graph with v vertices, \({v^2}\) edges and 8 faces, find v. Sketch a graph that fulfils all of these conditions.
▶️Answer/Explanation
Markscheme
(i) \(e \leqslant 3v – 6,{\text{ for }}v \geqslant 3\) A1A1
(ii) 
A1
(iii) 
A1
(iv) from Euler’s relation \(v – e + f = 2\)
\(v – {v^2} + 8 = 2\) M1
\({v^2} – v – 6 = 0\) A1
\((v + 2)(v – 3) = 0\)
\(v = 3\) A1
for example
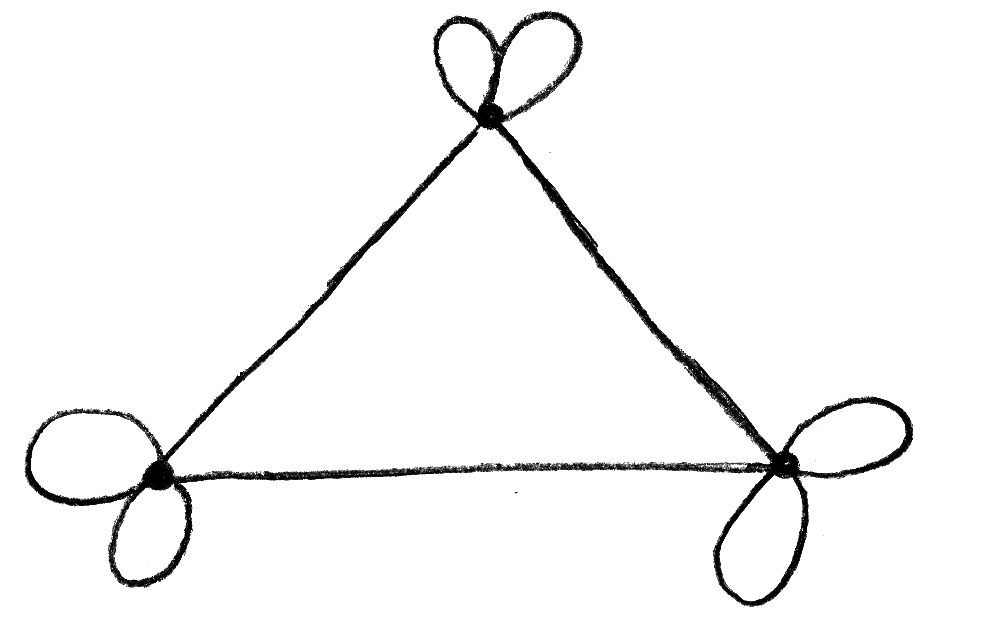A1
Note: There are many possible graphs.
[8 marks]
Examiners report
In (b) most candidates gave the required inequality although some just wrote down both inequalities from their formula booklet. The condition \(v \geqslant 3\) was less well known but could be deduced from the next 2 graphs. Euler’s relation was used well to obtain the quadratic to solve and many candidates could then draw a correct graph.
Question
Draw the complement of the following graph as a planar graph.
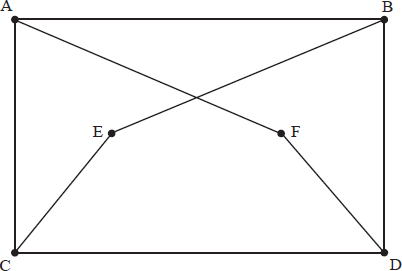
A simple graph G has v vertices and e edges. The complement \(G’\) of G has \({e’}\) edges.
(i) Prove that \(e \leqslant \frac{1}{2}v(v – 1)\) .
(ii) Find an expression for \(e + e’\) in terms of v .
(iii) Given that \({G’}\) is isomorphic to G , prove that v is of the form 4n or 4n + 1 for \(n \in {\mathbb{Z}^ + }\) .
(iv) Prove that there is a unique simple graph with 4 vertices which is isomorphic to its complement.
(v) Prove that if \(v \geqslant 11\) , then G and \({G’}\) cannot both be planar.
▶️Answer/Explanation
Markscheme
as a first step, form the following graph
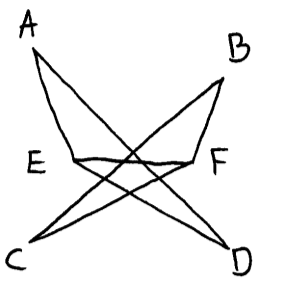(M1)(A1)
make it planar
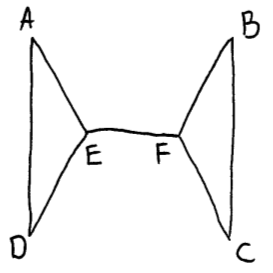A1
[3 marks]
(i) an edge joins a pair of vertices R1
there is a maximum of \(\left( {\begin{array}{*{20}{c}}
v \\
2
\end{array}} \right) = \frac{1}{2}v(v – 1)\) possible unordered pairs of vertices, hence displayed result A1AG
(ii) an edge joins two vertices in \({G’}\) if it does not join them in G and vice versa; all possible edges are accounted for by the union of the two graphs R1
\(e + e’ = \frac{1}{2}v(v – 1)\) A1
(iii) the two graphs have the same number of edges R1
\( \Rightarrow e = \frac{1}{4}v(v – 1)\) A1
v and v – 1 are consecutive integers, so only one can be divisible by 4, hence displayed result A1AG
(iv) the required graphs have four vertices and three edges A1
if one vertex is adjacent to the other three, that uses up the edges; the resulting graph, necessarily connected, has a disconnected complement, and vice versa R1
if one vertex is adjacent to two others, that uses up two edges; the final vertex cannot be adjacent to the first; the result is the linear connected graph A1
state it is isomorphic to its complement A1 N2
Note: Alternative proofs are possible, but should include the final statement for full marks.
(v) using \(e \leqslant 3v – 6\) for planar graphs M1
\(\frac{1}{2}v(v – 1) = e + e’ \leqslant 6v – 12\) A1
\({v^2} – 13v + 24 \leqslant 0\) is not possible for \(v \geqslant 11\) R1
[14 marks]
Examiners report
Part (a) was well done. The various parts of Parts (b) were often attempted, but with a disappointing feeling that the candidates did not have a confident understanding of what they were writing.
Part (a) was well done. The various parts of Parts (b) were often attempted, but with a disappointing feeling that the candidates did not have a confident understanding of what they were writing.
Question
A simple connected planar graph, has \(e\) edges, \(v\) vertices and \(f\) faces.
(i) Show that \(2e \ge 3f{\text{ if }}v > 2\).
(ii) Hence show that \({K_5}\), the complete graph on five vertices, is not planar.[6]
(i) State the handshaking lemma.
(ii) Determine the value of \(f\), if each vertex has degree \(2\).[4]
Draw an example of a simple connected planar graph on \(6\) vertices each of degree \(3\).[2]
▶️Answer/Explanation
Markscheme
(i) METHOD 1
attempting to use \(f = e – v + 2\) and \(e \le 3v – 6\) (if \(v > 2\)) (M1)
\(2e \le 6v – 12 = 6(e – f + 2) – 12\) M1A1
leading to \(2e \ge 3f\) AG
METHOD 2
each face is bounded by at least three edges A1
Note: Award A1 for stating \(e \ge 3f\).
each edge either separates two faces or, if an edge is interior to a face, it gets counted twice R1
Note: Award R1 for stating that each edge contributes two to the sum of the degrees of the faces (or equivalent) ie, \(\sum {\deg (F) = 2e} \).
adding up the edges around each face R1
leading to \(2e \ge 3f\) AG
(ii) \({K_5}\) has \(e = 10\) A1
if the graph is planar, \(f = 7\) A1
this contradicts the inequality obtained above R1
hence the graph is non-planar AG
[6 marks]
(i) the sum of the vertex degrees \( = 2e\) (or is even) or equivalent A1
(ii) if each vertex has degree \(2\), then \(2v = 2e\) A1
substituting \(v = e\) into Euler’s formula M1
\(f = 2\) A1
[4 marks]
for example,
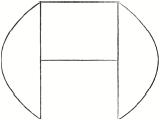A2
[2 marks]
Total [12 marks]
Examiners report
In part (a) (i), many candidates tried to prove \(2e \ge 3f\) with numerical examples. Only a few candidates were able to prove this inequality correctly. In part (a) (ii), most candidates knew that \({K_5}\) has 10 edges. However, a number of candidates simply drew a diagram with any number of faces and used this particular representation as a basis for their ‘proof’. Many candidates did not recognise the ‘hence’ requirement in part (a) (ii).
In part (b) (i), many candidates stated the ‘handshaking lemma’ incorrectly by relating it to the ‘handshake problem’. In part (b) (ii), only a few candidates determined that \(v = e\) and hence found that \(f = 2\).
In part (c), a reasonable number of candidates were able to draw a simple connected planar graph on \(6\) vertices each of degree \(3\). The most common error here was to produce a graph that contained a multiple edge(s).
Question
A simple connected planar graph, has \(e\) edges, \(v\) vertices and \(f\) faces.
(i) Show that \(2e \ge 3f{\text{ if }}v > 2\).
(ii) Hence show that \({K_5}\), the complete graph on five vertices, is not planar.[6]
(i) State the handshaking lemma.
(ii) Determine the value of \(f\), if each vertex has degree \(2\).[4]
Draw an example of a simple connected planar graph on \(6\) vertices each of degree \(3\).[2]
▶️Answer/Explanation
Markscheme
(i) METHOD 1
attempting to use \(f = e – v + 2\) and \(e \le 3v – 6\) (if \(v > 2\)) (M1)
\(2e \le 6v – 12 = 6(e – f + 2) – 12\) M1A1
leading to \(2e \ge 3f\) AG
METHOD 2
each face is bounded by at least three edges A1
Note: Award A1 for stating \(e \ge 3f\).
each edge either separates two faces or, if an edge is interior to a face, it gets counted twice R1
Note: Award R1 for stating that each edge contributes two to the sum of the degrees of the faces (or equivalent) ie, \(\sum {\deg (F) = 2e} \).
adding up the edges around each face R1
leading to \(2e \ge 3f\) AG
(ii) \({K_5}\) has \(e = 10\) A1
if the graph is planar, \(f = 7\) A1
this contradicts the inequality obtained above R1
hence the graph is non-planar AG
[6 marks]
(i) the sum of the vertex degrees \( = 2e\) (or is even) or equivalent A1
(ii) if each vertex has degree \(2\), then \(2v = 2e\) A1
substituting \(v = e\) into Euler’s formula M1
\(f = 2\) A1
[4 marks]
for example,
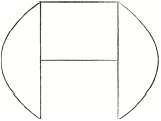A2
[2 marks]
Total [12 marks]
Examiners report
In part (a) (i), many candidates tried to prove \(2e \ge 3f\) with numerical examples. Only a few candidates were able to prove this inequality correctly. In part (a) (ii), most candidates knew that \({K_5}\) has 10 edges. However, a number of candidates simply drew a diagram with any number of faces and used this particular representation as a basis for their ‘proof’. Many candidates did not recognise the ‘hence’ requirement in part (a) (ii).
In part (b) (i), many candidates stated the ‘handshaking lemma’ incorrectly by relating it to the ‘handshake problem’. In part (b) (ii), only a few candidates determined that \(v = e\) and hence found that \(f = 2\).
In part (c), a reasonable number of candidates were able to draw a simple connected planar graph on \(6\) vertices each of degree \(3\). The most common error here was to produce a graph that contained a multiple edge(s).