Download IITian Academy App for accessing Online Mock Tests and More..
Question
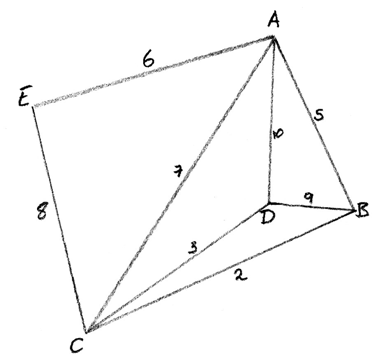
The table below shows the distances between towns A, B, C, D and E.
(i) Draw the graph, in its planar form, that is represented by the table.
(ii) Write down with reasons whether or not it is possible to find an Eulerian trail in this graph.
(iii) Solve the Chinese postman problem with reference to this graph if A is to be the starting and finishing point. Write down the walk and determine the length of the walk.
Show that a graph cannot have exactly one vertex of odd degree.
Answer/Explanation
Markscheme
(i)
A1A1A1
Note: Award A1 for the vertices, A1 for edges and A1 for planar form.
(ii) It is possible to find an Eulerian trail in this graph since exactly two of the vertices have odd degree R1
(iii) B and D are the odd vertices M1
\(BC + CD = 3 + 2 = 5{\text{ and }}BD = 9,\) A1
since 5 < 9 , BC and CD must be traversed twice R1
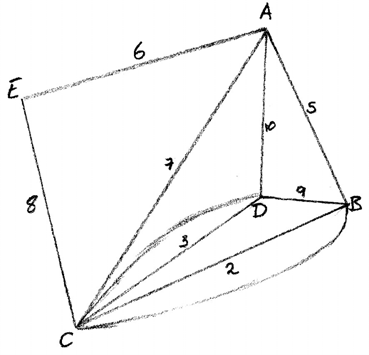
A possible walk by inspection is ACBDABCDCEA A1
This gives a total length of
2(2 + 3) + 8 + 9 + 5 + 7 + 10 + 6 = 55 for the walk A1
[9 marks]
The sum of all the vertex degrees is twice the number of edges, i.e. an even number.
Hence a graph cannot have exactly one vertex of odd degree. M1R1
[2 marks]
Examiners report
Drawing the graph usually presented no difficulty. Distinguishing between Eulerian and semi-Eulerian needs attention but this part was usually done successfully.
A simple, clear argument for part (c) was often hidden in mini-essays on graph theory.
Drawing the graph usually presented no difficulty. Distinguishing between Eulerian and semi-Eulerian needs attention but this part was usually done successfully.
A simple, clear argument for part (c) was often hidden in mini-essays on graph theory.
Question
In any graph, show that
(i) the sum of the degrees of all the vertices is even;
(ii) there is an even number of vertices of odd degree.
Consider the following graph, M.
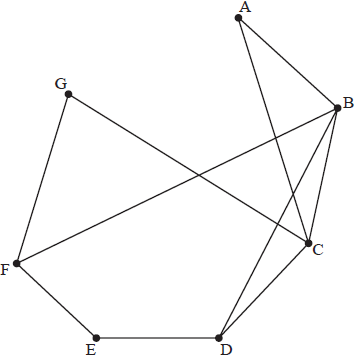
(i) Show that M is planar.
(ii) Explain why M is not Eulerian.
(iii) By adding one edge to M it is possible to make it Eulerian. State which edge must be added.
This new graph is called N.
(iv) Starting at A, write down a possible Eulerian circuit for N.
(v) Define a Hamiltonian cycle. If possible, write down a Hamiltonian cycle for N, and if not possible, give a reason.
(vi) Write down the adjacency matrix for N.
(vii) Which pair of distinct vertices has exactly 30 walks of length 4 between them?
Answer/Explanation
Markscheme
(i) When we sum over the degrees of all vertices, we count each edge twice. Hence every edge adds two to the sum. Hence the sum of the degrees of all the vertices is even. R2
(ii) divide the vertices into two sets, those with even degree and those with odd degree M1
let S be the sum of the degrees of the first set and let T be the sum of the degrees of the second set
we know S + T must be even
since S is the sum of even numbers, then it is even R1
hence T must be even R1
hence there must be an even number of vertices of odd degree AG
[5 marks]
(i)
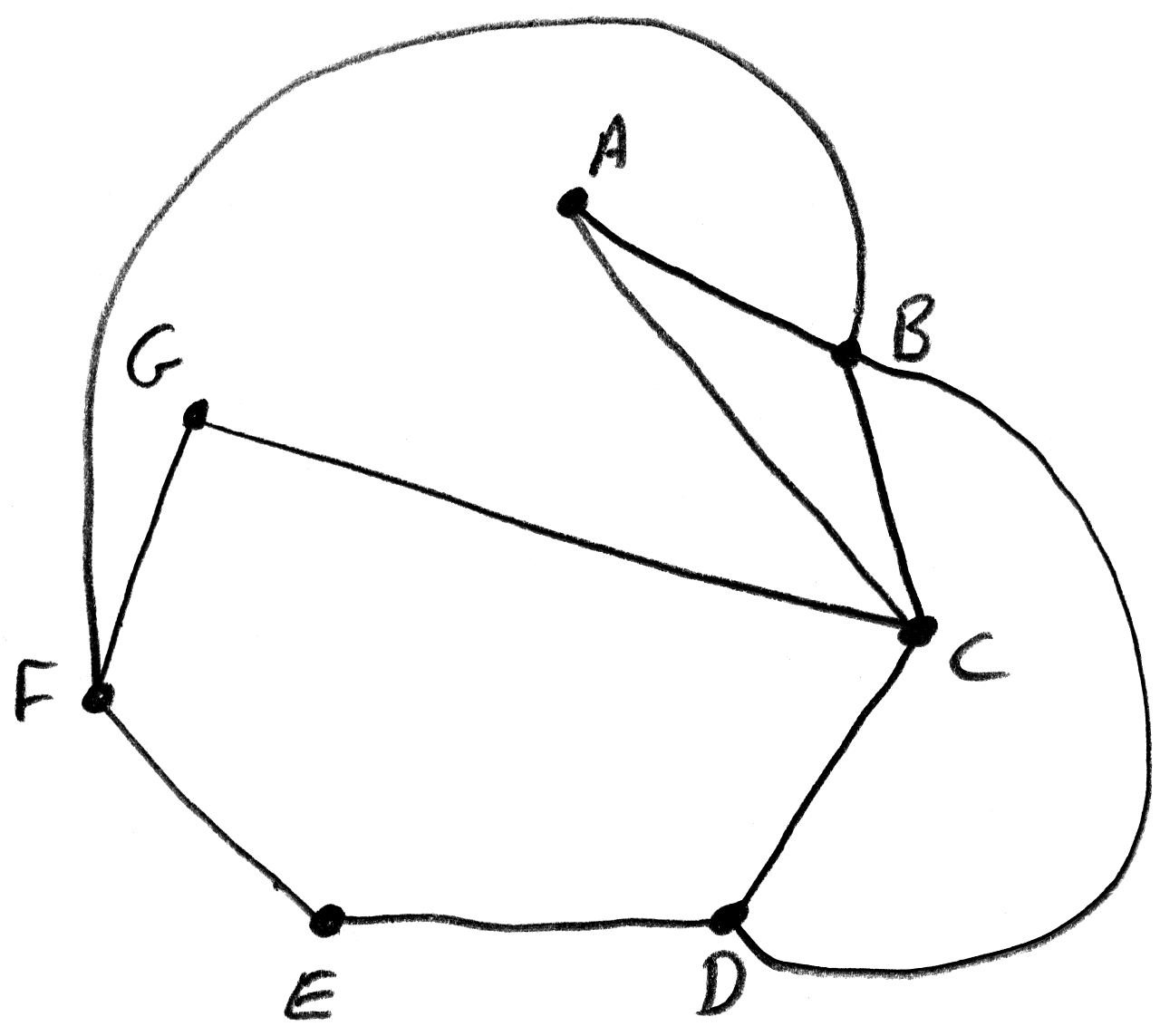A1
(ii) the graph M is not Eulerian because vertices D and F are of odd degree A1
(iii) the edge which must be added is DF A1
(iv)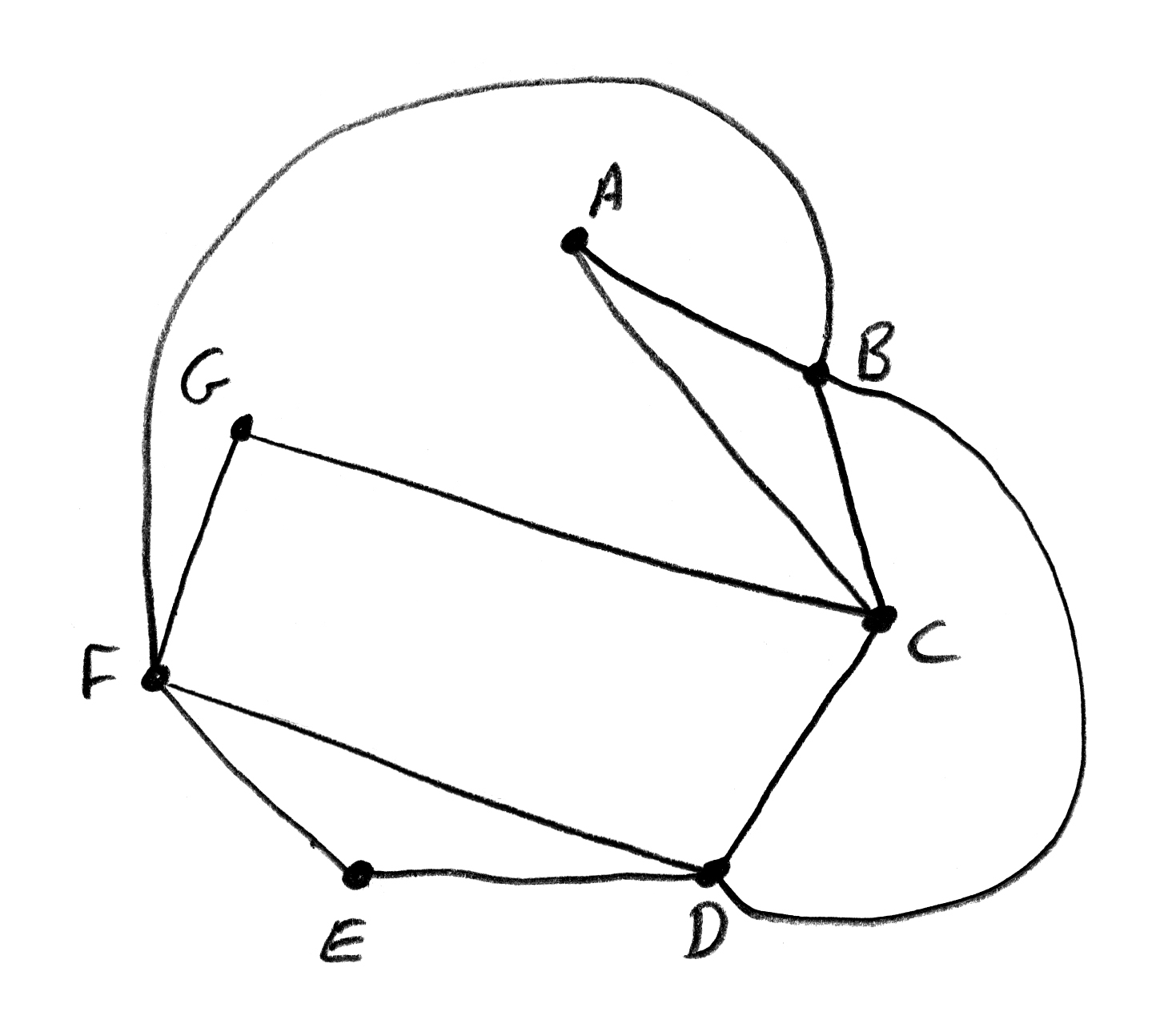
a possible Eulerian circuit is ABDFBCDEFGCA A2
Note: award A1 for a correct Eulerian circuit not starting and finishing at A.
(v) a Hamiltonian cycle is one that contains each vertex in N A1
with the exception of the starting and ending vertices, each vertex must only appear once A1
a possible Hamiltonian cycle is ACGFEDBA A1
(vi) \(\left( {\begin{array}{*{20}{c}}
0&1&1&0&0&0&0 \\
1&0&1&1&0&1&0 \\
1&1&0&1&0&0&1 \\
0&1&1&0&1&1&0 \\
0&0&0&1&0&1&0 \\
0&1&0&1&1&0&1 \\
0&0&1&0&0&1&0
\end{array}} \right)\) A2
(vii) using adjacency matrix to power 4 (M1)
C and F A1
[12 marks]
Examiners report
Most candidates were able to start (a), but many found problems in expressing their ideas clearly in words. Stronger candidates had little problem with (b), but a significant number of weaker candidates had problems working with the concepts of Eulerian circuits and Hamiltonian cycles and with understanding how to find a specific number of walks of a certain length as required in (b) (vii).
Most candidates were able to start (a), but many found problems in expressing their ideas clearly in words. Stronger candidates had little problem with (b), but a significant number of weaker candidates had problems working with the concepts of Eulerian circuits and Hamiltonian cycles and with understanding how to find a specific number of walks of a certain length as required in (b) (vii).
Question
The graph G has adjacency matrix M given below.
Draw the graph G .
What information about G is contained in the diagonal elements of M\(^2\) ?
List the trails of length 4 starting at A and ending at C.
Answer/Explanation
Markscheme
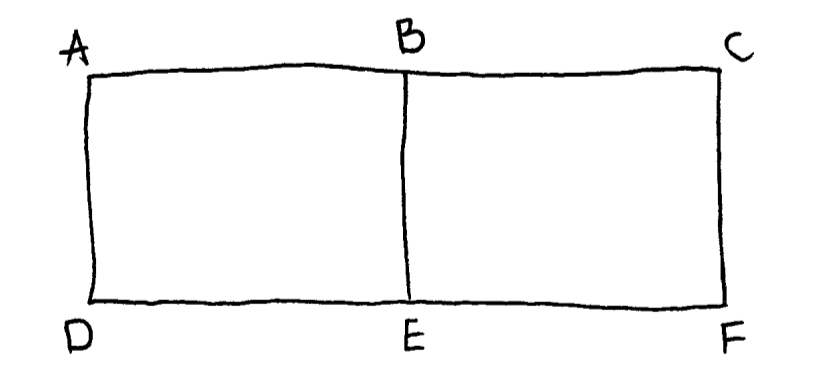A2
Note: Award A1 if only one error, A0 for two or more.
[2 marks]
the (k, k) element of M\(^2\) is the number of vertices directly connected to vertex k A1
Note: Accept comment about the number of walks of length 2, in which the initial and final vertices coincide.
[1 mark]
the trails of length 4 are ABEDC, AFEDC, AFEBC A1A1A1
Note: A1A1A1 for three correct with no additions; A1A1A0 for all correct, but with additions; A1A0A0 for two correct with or without additions.
[3 marks]
Examiners report
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
Question
Draw the complement of the following graph as a planar graph.
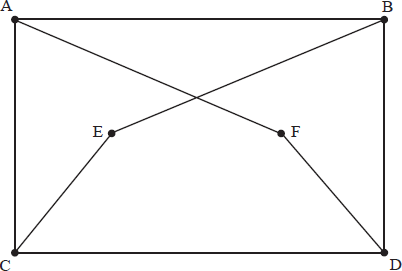
A simple graph G has v vertices and e edges. The complement \(G’\) of G has \({e’}\) edges.
(i) Prove that \(e \leqslant \frac{1}{2}v(v – 1)\) .
(ii) Find an expression for \(e + e’\) in terms of v .
(iii) Given that \({G’}\) is isomorphic to G , prove that v is of the form 4n or 4n + 1 for \(n \in {\mathbb{Z}^ + }\) .
(iv) Prove that there is a unique simple graph with 4 vertices which is isomorphic to its complement.
(v) Prove that if \(v \geqslant 11\) , then G and \({G’}\) cannot both be planar.
Answer/Explanation
Markscheme
as a first step, form the following graph
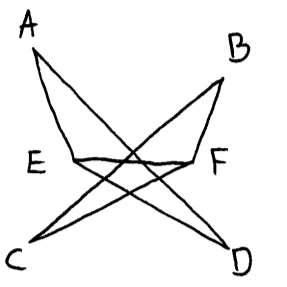(M1)(A1)
make it planar
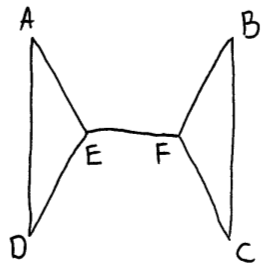A1
[3 marks]
(i) an edge joins a pair of vertices R1
there is a maximum of \(\left( {\begin{array}{*{20}{c}}
v \\
2
\end{array}} \right) = \frac{1}{2}v(v – 1)\) possible unordered pairs of vertices, hence displayed result A1AG
(ii) an edge joins two vertices in \({G’}\) if it does not join them in G and vice versa; all possible edges are accounted for by the union of the two graphs R1
\(e + e’ = \frac{1}{2}v(v – 1)\) A1
(iii) the two graphs have the same number of edges R1
\( \Rightarrow e = \frac{1}{4}v(v – 1)\) A1
v and v – 1 are consecutive integers, so only one can be divisible by 4, hence displayed result A1AG
(iv) the required graphs have four vertices and three edges A1
if one vertex is adjacent to the other three, that uses up the edges; the resulting graph, necessarily connected, has a disconnected complement, and vice versa R1
if one vertex is adjacent to two others, that uses up two edges; the final vertex cannot be adjacent to the first; the result is the linear connected graph A1
state it is isomorphic to its complement A1 N2
Note: Alternative proofs are possible, but should include the final statement for full marks.
(v) using \(e \leqslant 3v – 6\) for planar graphs M1
\(\frac{1}{2}v(v – 1) = e + e’ \leqslant 6v – 12\) A1
\({v^2} – 13v + 24 \leqslant 0\) is not possible for \(v \geqslant 11\) R1
[14 marks]
Examiners report
Part (a) was well done. The various parts of Parts (b) were often attempted, but with a disappointing feeling that the candidates did not have a confident understanding of what they were writing.
Part (a) was well done. The various parts of Parts (b) were often attempted, but with a disappointing feeling that the candidates did not have a confident understanding of what they were writing.
Question
Use the pigeon-hole principle to prove that for any simple graph that has two or more vertices and in which every vertex is connected to at least one other vertex, there must be at least two vertices with the same degree.
Seventeen people attend a meeting.
Each person shakes hands with at least one other person and no-one shakes hands with
the same person more than once. Use the result from part (a) to show that there must be at least two people who shake hands with the same number of people.
Explain why each person cannot have shaken hands with exactly nine other people.
Answer/Explanation
Markscheme
let there be \(v\) vertices in the graph; because the graph is simple the degree of each vertex is \( \le v – 1\) A1
the degree of each vertex is \( \ge 1\) A1
there are therefore \(v – 1\) possible values for the degree of each vertex A1
given there are \(v\) vertices by the pigeon-hole principle there must be at least two with the same degree R1
[4 marks]
consider a graph in which the people at the meeting are represented by the vertices and two vertices are connected if the two people shake hands M1
the graph is simple as no-one shakes hands with the same person more than once (nor can someone shake hands with themselves) A1
every vertex is connected to at least one other vertex as everyone shakes at least one hand A1
the degree of each vertex is the number of handshakes so by the proof above there must be at least two who shake the same number of hands R1
Note: Accept answers starting afresh rather than quoting part (a).
[4 marks]
(the handshaking lemma tells us that) the sum of the degrees of the vertices must be an even number A1
the degree of each vertex would be \(9\) and \(9 \times 17\) is an odd number (giving a contradiction) A1
[2 marks]
Total [10 marks]
Examiners report
Generally there were too many “waffly” words and not enough precise statements leading to conclusions.
Misconceptions were: thinking that a few examples constituted a proof, thinking that the graph had to be connected, taking the edges as the pigeons not the degrees. The pigeon-hole principle was known but not always applied well.
Generally there were too many “waffly” words and not enough precise statements leading to conclusions.
Similar problems as in (a).
Generally there were too many “waffly” words and not enough precise statements leading to conclusions.
Many spurious reasons were given but good candidates went straight to the hand-shaking lemma.
Question
A simple connected planar graph, has \(e\) edges, \(v\) vertices and \(f\) faces.
(i) Show that \(2e \ge 3f{\text{ if }}v > 2\).
(ii) Hence show that \({K_5}\), the complete graph on five vertices, is not planar.
(i) State the handshaking lemma.
(ii) Determine the value of \(f\), if each vertex has degree \(2\).
Draw an example of a simple connected planar graph on \(6\) vertices each of degree \(3\).
Answer/Explanation
Markscheme
(i) METHOD 1
attempting to use \(f = e – v + 2\) and \(e \le 3v – 6\) (if \(v > 2\)) (M1)
\(2e \le 6v – 12 = 6(e – f + 2) – 12\) M1A1
leading to \(2e \ge 3f\) AG
METHOD 2
each face is bounded by at least three edges A1
Note: Award A1 for stating \(e \ge 3f\).
each edge either separates two faces or, if an edge is interior to a face, it gets counted twice R1
Note: Award R1 for stating that each edge contributes two to the sum of the degrees of the faces (or equivalent) ie, \(\sum {\deg (F) = 2e} \).
adding up the edges around each face R1
leading to \(2e \ge 3f\) AG
(ii) \({K_5}\) has \(e = 10\) A1
if the graph is planar, \(f = 7\) A1
this contradicts the inequality obtained above R1
hence the graph is non-planar AG
[6 marks]
(i) the sum of the vertex degrees \( = 2e\) (or is even) or equivalent A1
(ii) if each vertex has degree \(2\), then \(2v = 2e\) A1
substituting \(v = e\) into Euler’s formula M1
\(f = 2\) A1
[4 marks]
for example,
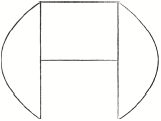A2
[2 marks]
Total [12 marks]
Examiners report
In part (a) (i), many candidates tried to prove \(2e \ge 3f\) with numerical examples. Only a few candidates were able to prove this inequality correctly. In part (a) (ii), most candidates knew that \({K_5}\) has 10 edges. However, a number of candidates simply drew a diagram with any number of faces and used this particular representation as a basis for their ‘proof’. Many candidates did not recognise the ‘hence’ requirement in part (a) (ii).
In part (b) (i), many candidates stated the ‘handshaking lemma’ incorrectly by relating it to the ‘handshake problem’. In part (b) (ii), only a few candidates determined that \(v = e\) and hence found that \(f = 2\).
In part (c), a reasonable number of candidates were able to draw a simple connected planar graph on \(6\) vertices each of degree \(3\). The most common error here was to produce a graph that contained a multiple edge(s).
Question
The simple, connected graph \(G\) has e edges and \(v\) vertices, where \(v \geqslant 3\).
Given that both \(G\) and \(G’\) are planar and connected,
Show that the number of edges in \(G’\), the complement of \(G\), is \(\frac{1}{2}{v^2} – \frac{1}{2}v – e\).
show that the sum of the number of faces in \(G\) and the number of faces in \(G’\) is independent of \(e\);
show that \({v^2} – 13v + 24 \leqslant 0\) and hence determine the maximum possible value of \(v\).
Answer/Explanation
Markscheme
the total number of edges in \(G\) and \(G’\) is \(\frac{{v(v – 1)}}{2}\) (A1)
the number of edges in \(G’ = \frac{{v(v – 1)}}{2} – e\) A1
\( = \frac{1}{2}{v^2} – \frac{1}{2}v – e\) AG
[2 marks]
using Euler’s formula, number of faces in \(G = e + 2 – v\) A1
number of faces in \(G’ = \frac{{{v^2}}}{2} – \frac{v}{2} – e + 2 – v\) A1
sum of these numbers \( = \frac{{{v^2}}}{2} – \frac{{5v}}{2} + 4\) A1
this is independent of \(e\) AG
[3 marks]
for \(G\) to be planar, we require (M1)
\(e \leqslant 3v – 6\) A1
for \(e \leqslant 3v – 6\) to be planar, we require
\(\frac{{{v^2}}}{2} – \frac{v}{2} – e \leqslant 3v – 6\) A1
for these two inequalities to be satisfied simultaneously, adding or substituting we require
\(\frac{{{v^2}}}{2} – \frac{v}{2} \leqslant 6v – 12\) (M1)A1
leading to \({v^2} – 13v + 24 \leqslant 0\) AG
the roots of the equation are 10.8 (and 2.23) (A1)
the largest value of \(v\) is therefore 10 A1
[7 marks]
Examiners report
Generally in this question, good candidates thought their way through it whereas weak candidates just wrote down anything they could off the formula booklet or drew pictures of particular graphs. It was important to keep good notation and not let the same symbol stand for different things.
(a) If they considered the complete graph they were fine.
Generally in this question, good candidates thought their way through it whereas weak candidates just wrote down anything they could off the formula booklet or drew pictures of particular graphs. It was important to keep good notation and not let the same symbol stand for different things.
(b) Some confusion here if they were not clear about which graph they were applying Euler’s formula to. If they were methodical with good notation they obtained the answer.
Generally in this question, good candidates thought their way through it whereas weak candidates just wrote down anything they could off the formula booklet or drew pictures of particular graphs. It was important to keep good notation and not let the same symbol stand for different things.
(c) Again the same confusion about applying the inequality to both graphs. Most candidates realised which inequality was applicable. Many candidates had the good exam technique to pick up the last two marks even if they did not obtain the quadratic inequality.
Question
In this question no graphs are required to be drawn. Use the handshaking lemma and other results about graphs to explain why,
a graph cannot exist with a degree sequence of \(1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6,{\text{ }}7,{\text{ }}8,{\text{ }}9\);
a simple, connected, planar graph cannot exist with a degree sequence of \(4,{\text{ }}4,{\text{ }}4,{\text{ }}4,{\text{ }}5,{\text{ }}5\);
a tree cannot exist with a degree sequence of \(1,{\text{ }}1,{\text{ }}2,{\text{ }}2,{\text{ }}3,{\text{ }}3\).
Answer/Explanation
Markscheme
assume such a graph exists
by the handshaking lemma the sum of the degrees equals twice the number of edges R1
but \(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45\) which is odd R1
this is a contradiction so graph does not exist AG
[2 marks]
assume such a graph exists
since the graph is simple and connected (and \(v = 6 > 2\)) then \(e \leqslant 3v – 6\) R1
by the handshaking lemma \(4 + 4 + 4 + 4 + 5 + 5 = 2e\) so \(e = 13\) A1
hence \(13 \leqslant 3 \times 6 – 6 = 12\) A1
this is a contradiction so graph does not exist AG
[3 marks]
assume such a graph exists
a tree with 6 vertices must have 5 edges (since \({\text{V}} – {\text{E}} + 1 = 2\) for a tree) R1
using the Handshaking Lemma \(1 + 1 + 2 + 2 + 3 + 3 = 2 \times 5\) implies \(12 = 10\) M1A1
this is a contradiction so graph does not exist AG
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider the complete bipartite graph \({\kappa _{3,\,3}}\).
Draw \({\kappa _{3,\,3}}\).
Show that \({\kappa _{3,\,3}}\) has a Hamiltonian cycle.
Draw \({\kappa _{3,\,2}}\) and explain why it does not have a Hamiltonian cycle.
In the context of graph theory, state the handshaking lemma.
Hence show that a graph G with degree sequence 2, 3, 3, 4, 4, 5 cannot exist.
Let T be a tree with \(v\) where \(v\) ≥ 2.
Use the handshaking lemma to prove that T has at least two vertices of degree one.
Answer/Explanation
Markscheme
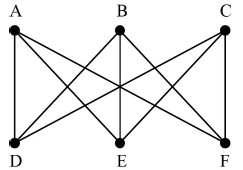A1
[1 mark]
for example ADBECFA A1
Note: Accept drawing the cycle on their diagram.
Note: Accept Dirac’s theorem (although it is not on the syllabus for (a)(ii). There is no converse that could be applied for (a)(iii).
[1 mark]
A1
a Hamiltonian cycle would have to alternate between the two vertex subsets which is impossible as 2 ≠ 3 R1
Note: Award R1 for an attempt to construct a Hamiltonian cycle and an explanation of why it fails, eg, ADBEC but there is no route from C to A without re-using D or E so no cycle. There are other proofs eg, have to go in and out of A, similarly B and C giving all edges leading to a contradiction.
[2 marks]
the sum of the vertex degrees is twice the number of edges A1
[1 mark]
assume G exists
the sum 2 + 3 + 3 + 4 + 4 + 5 = 21 A1
this is odd (not even) R1
this contradicts the handshaking lemma
so G does not exist AG
[2 marks]
T has \(v – 1\) edges A1
EITHER
if \(k\) vertices have degree 1 then \(v – k\) vertices have degree ≥ 2 R1
by the handshaking lemma
\(2v – 2 \geqslant 1 \times k + 2\left( {v – k} \right)\left( { = 2v – k} \right)\) M1
this gives \(k\) ≥ 2 A1
OR
let S be the sum of vertex degrees
consider T having either no or one vertex of degree 1 R1
case 1 suppose T has no vertices of degree 1 (eg, all vertices have degrees ≥ 2)
by the handshaking lemma
\(S \geqslant 2v \ne 2\left( {v – 1} \right)\) (not possible) A1
case 2 suppose T has one vertex of degree 1 (eg, \(v – 1\) vertices have degrees ≥ 2)
by the handshaking lemma
\(S \geqslant 2\left( {v – 1} \right) + 1 \ne 2\left( {v – 1} \right)\) (not possible) A1
THEN
so T has at least two vertices of degree 1 AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]