Question
(a) Sketch the curve \(f(x) = \left| {1 + 3\sin (2x)} \right|{\text{, for }}0 \leqslant x \leqslant \pi \) . Write down on the graph the values of the x and y intercepts.
(b) By adding one suitable line to your sketch, find the number of solutions to the equation \(\pi f(x) = 4(\pi – x)\) .
▶️Answer/Explanation
Markscheme
(a)
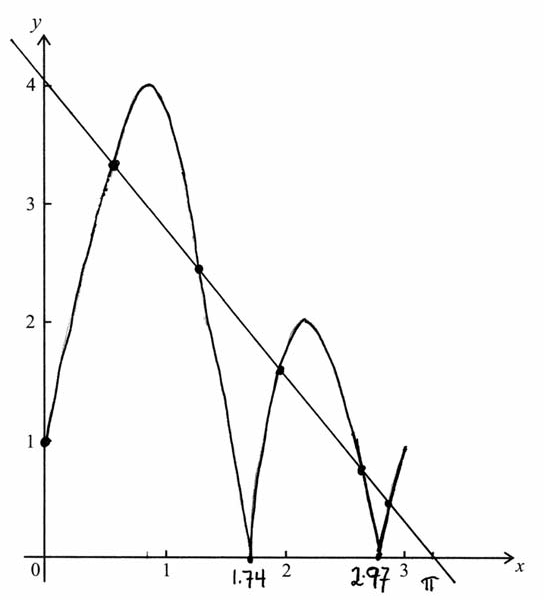A1A1A1A1
Note: Award A1 for y-intercept
A1A1 for x-intercepts
A1 for shape
(b) correct line A1
5 solutions A1
[6 marks]
Examiners report
Part (a) was well executed by the majority of candidates. Most candidates had the correct graph with the correct x and y intercepts. For part (b), some candidates had the straight line intersect the x-axis at 3 rather than at \(\pi \) , and hence did not observe that there were 5 points of intersection.
Question
(a) Sketch the curve \(y = \left| {\ln x} \right| – \left| {\cos x} \right| – 0.1\) , \(0 < x < 4\) showing clearly the coordinates of the points of intersection with the x-axis and the coordinates of any local maxima and minima.
(b) Find the values of x for which \(\left| {\ln x} \right| > \left| {\cos x} \right| + 0.1\), \(0 < x < 4\) .
▶️Answer/Explanation
Markscheme
(a)
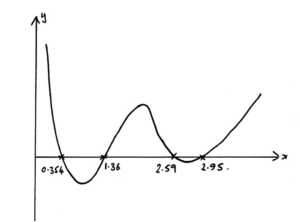A1
Note: Award A1 for shape.
x-intercepts 0.354, 1.36, 2.59, 2.95 A2
Note: Award A1 for three correct, A0 otherwise.
maximum = (1.57, 0.352) = \(\left( {\frac{\pi }{2},0.352} \right)\) A1
minimum = (1, – 0.640) and (2.77, – 0.0129) A1
(b) \(0 < x < 0.354,{\text{ }}1.36 < x < 2.59,{\text{ }}2.95 < x < 4\) A2
Note: Award A1 if two correct regions given.
[7 marks]
Examiners report
Solutions to this question were extremely disappointing with many candidates doing the sketch in degree mode instead of radian mode. The two adjacent intercepts at 2.59 and 2.95 were often missed due to an unsatisfactory window. Some sketches were so small that a magnifying glass was required to read some of the numbers; candidates would be well advised to draw sketches large enough to be easily read.
Question
Sketch the graph of \(f(x) = x + \frac{{8x}}{{{x^2} – 9}}\). Clearly mark the coordinates of the two maximum points and the two minimum points. Clearly mark and state the equations of the vertical asymptotes and the oblique asymptote.
▶️Answer/Explanation
Markscheme
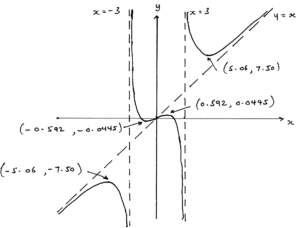M1A1A1A1A1A1A1
Note: Award A1 for both vertical asymptotes correct,
M1 for recognizing that there are two turning points near the origin,
A1 for both turning points near the origin correct, (only this A mark is dependent on the M mark)
A1 for the other pair of turning points correct,
A1 for correct positioning of the oblique asymptote,
A1 for correct equation of the oblique asymptote,
A1 for correct asymptotic behaviour in all sections.
[7 marks]
Examiners report
This question was generally well done, except for the behaviour near the origin. The questions alerted candidates to the existence of four turning points and an oblique asymptote, but not all reported back on this information.
Question
Consider the graph of \(y = x + \sin (x – 3),{\text{ }} – \pi \leqslant x \leqslant \pi \).
a.Sketch the graph, clearly labelling the x and y intercepts with their values.[3]
b.Find the area of the region bounded by the graph and the x and y axes.[2]
▶️Answer/Explanation
Markscheme
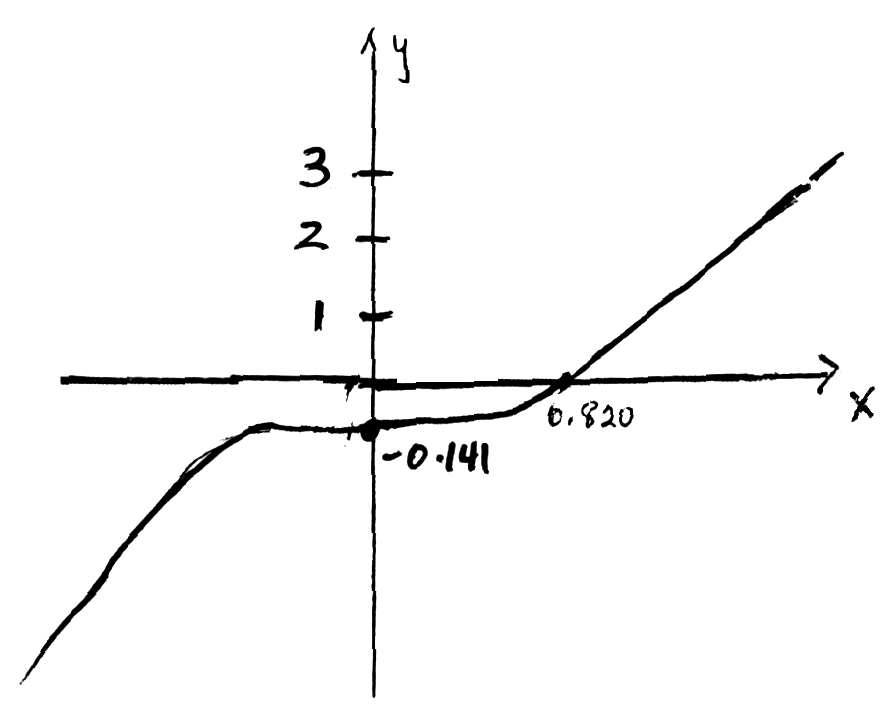A1A1A1
Note: Award A1 for shape,
A1 for x-intercept is 0.820, accept \(\sin ( – 3){\text{ or }} – \sin (3)\)
A1 for y-intercept is −0.141.
[3 marks]
\(A = \int_0^{0.8202} {\left| {x + \sin (x – 3)} \right|{\text{d}}x \approx 0.0816{\text{ sq units}}} \) (M1)A1
[2 marks]