Question
Find the values of x for which |5-3x|≤|x+1|.
▶️Answer/Explanation
AnsMETHOD 1
\(|5-3x|\leq|x+1|\Rightarrow 25-30x+9x^2\leq x^2+2x+1\)
\(\Rightarrow 8x^2-32x+24\leq 0\Rightarrow 8(x-1)(x-3)\leq 0\)
\(\Rightarrow 1\leq x\leq 3\)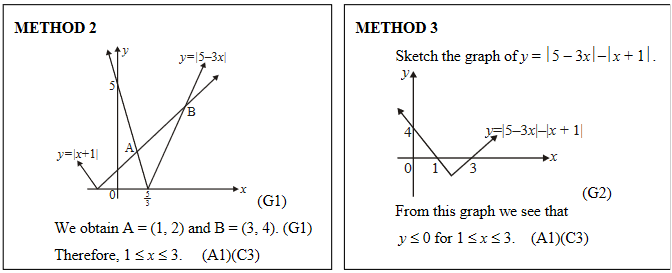
Question
Solve the inequality |x-2|≥|2x+1|.
▶️Answer/Explanation
Ans
METHOD 1
The graphs of y = |x-2| and y = |2x+1| meet where
(x-2)=(2x+1)=>x=-3
(x-2)=-(2x+1)=>x=\(\frac{1}{3}\)
Test any value, e.g. x = 0 satisfies inequality
so x ∈ \([-3, \frac{1}{3}]\).
METHOD 2
\((x-2)^2\geq (2x+1)^2\Rightarrow x^2-4x+4\geq 4x^2+4x+1\)
\(3x^2+8x-3\leq 0\Rightarrow (3x-1)(x+3)\leq 0\) (or find roots of equation)
Test any value , e.g. x = 0 satisfies inequality.
so x ∈ \([-3,\frac{1}{3}]\).
METHOD 3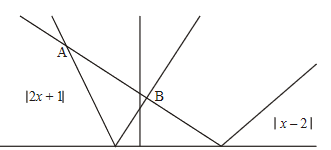
We obtain for A, x=-3 and for B, \(x=\frac{1}{3}\)
From the graph, x ∈ \([-3,\frac{1}{3}]\).
Question
Solve the inequality \(|\frac{x+9}{x-9}|≤2\).
▶️Answer/Explanation
Ans
METHOD 1
The critical values occur when \(\frac{x+9}{x-9}=±2→x=3,27\)
Consider [-∞,3]: value of function at 0 is 1 which is ≤ 2.
Consider [3,27]: value of function at 12 is 7 which is not ≤ 2.
Consider [27,∞]: value of function at 36 is \(\frac{5}{3}\) which is ≤2.
The required solution set is therefore[-∞,3]∪[27,∞].
METHOD 2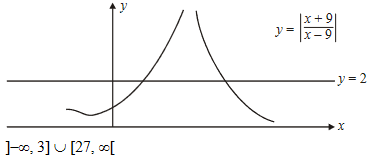
Question
Find the largest set of values of x such that the function f given by f(x)=\(\sqrt{\fra{8x-4}{x-3}}\) takes real values.
▶️Answer/Explanation
Ans
either algebraically or graphically: x ≤ 0.5 or x > 3
