Question
The following diagram shows the graph of y = arctan( \(2x+1+\frac{\pi}{4} \)) for \(x \in \mathbb{R}\) with asymptotes at \(y=-\frac{\pi}{4}\) and \(y=\frac{3\pi}{4}\)
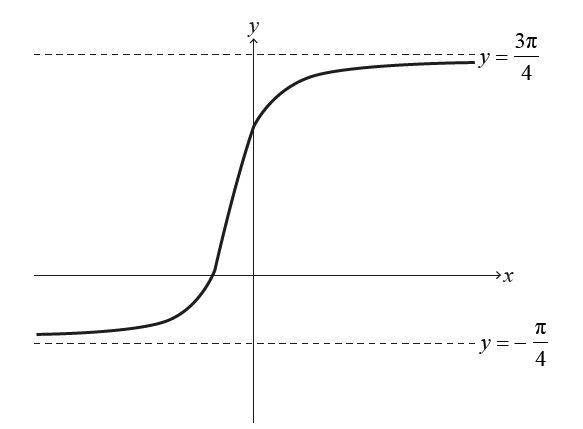
(a) Describe a sequence of transformations that transforms the graph of y = arctan x to the graph of y = arctan( \(2x+1+\frac{\pi}{4} \)) for \(x \in \mathbb{R}\) [3]
(b) Show that arctan arctan p+ arctan q= arctan \(\frac{p+q}{1-pq}\) where p , q > 0 and pq < 1 [4]
(c) Verify that \(arctan(2x+1) = arctan(\frac{x}{x+1})+\frac{\pi}{4}\) for x ∈ \(\mathbb{R}\) , x > 0 . [3]
(d) Using mathematical induction and the result from part (b), prove that
\(\sum_{r=1}^{n}arctan\frac{1}{2r^2}=arctan\frac{n}{n+1}\) for n ∈ \(\mathbb{Z}^+\)
Answer/Explanation
Ans:
(a) By replacing the $x$ in $y=\arctan x$ with $x+1$, we obtain $y=\arctan \left(x+1\right)$, which is a translation of $-1$ units parallel to the $x$-axis.
Next, by replacing the $x$ in $y=\arctan \left(x+1\right)$ with $2x$, we obtain $y=\arctan \left(2x+1\right)$, which is a stretch parallel to the $x$-axis by scale factor $\frac{1}{2}$.
Finally, by replacing the $y$ in $y=\arctan \left(2x+1\right)$ with $y-\frac{\pi}{4}$, we obtain $y-\frac{\pi}{4}=\arctan \left(2x+1\right)$, i.e., $y=\arctan \left(2x+1\right)+\frac{\pi}{4}$, which is a translation of $\frac{\pi}{4}$ units parallel to the $y$-axis.<br>
(b) Taking tangent on both sides in $\arctan p+\arctan q=\arctan\left(\frac{p+q}{1-pq}\right)$, we have $\tan\left(\arctan p+\arctan q\right)=\frac{p+q}{1-pq}$
$$\begin{eqnarray}
\text{LHS} &=& \tan\left(\arctan p+\arctan q\right) \nonumber \\
&=& \frac{p+q}{1-pq} \nonumber \\
&=& \text{RHS}.
\end{eqnarray}$$
(c) Observe that $\arctan 1=\frac{\pi}{4}$. Then, using (b), we have
$$\begin{eqnarray}
\text{RHS} &=& \arctan \left(\frac{x}{x+1}\right)+\frac{\pi}{4} \nonumber \\
&=& \arctan \left(\frac{x}{x+1}\right)+\arctan 1 \nonumber \\
&=& \arctan \left(\frac{1+\frac{x}{x+1}}{1-\frac{x}{x+1}}\right) \nonumber \\
&=& \arctan \left(\frac{2x+1}{x+1-x}\right) \nonumber \\
&=& \arctan \left(2x+1\right) \nonumber \\
&=& \text{LHS}.
\end{eqnarray}$$
(d) Let $\text{P}_n$ be the proposition “$\sum_{r=1}^{n} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{n}{n+1}\right)$” for $n\in\mathbb{Z}^+$.<br>
When $n=1$,<br>
$$\begin{eqnarray}
\text{LHS}=\sum_{r=1}^{1} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{1}{2}\right) \nonumber \\
\text{RHS}=\arctan\left(\frac{1}{1+1}\right)=\arctan\left(\frac{1}{2}\right).
\end{eqnarray}$$
Since $\text{LHS}=\text{RHS}$, $\text{P}_1$ is true.<br>
Assume that $\text{P}_k$ is true for some $k\in\mathbb{Z}^+$, i.e.,
$$\begin{eqnarray}
\sum_{r=1}^{k} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{k}{k+1}\right).
\end{eqnarray}$$
To show that $\text{P}_{k+1}$ is also true, i.e.,
$$\begin{eqnarray}
\sum_{r=1}^{k+1} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{k+1}{k+2}\right).
\end{eqnarray}$$
$$\begin{eqnarray}
\text{LHS} &=& \sum_{r=1}^{k+1} \arctan\left(\frac{1}{2r^2}\right) \nonumber \\
&=& \arctan\left(\frac{k}{k+1}\right)+\arctan\left(\frac{1}{2\left(k+1\right)^2}\right) \nonumber \\
&=& \arctan \left[\frac{\frac{k}{k+1}+\frac{1}{2\left(k+1\right)^2}}{1-\frac{k}{2\left(k+1\right)^3}}\right] \nonumber \\
&=& \arctan \left[\frac{2k\left(k+1\right)^2+\left(k+1\right)}{2\left(k+1\right)^3-k}\right] \nonumber \\
&=& \arctan \left[\frac{\left(k+1\right)\left(2k^2+2k+1\right)}{\left(k+2\right)\left(2k^2+2k+1\right)}\right] \nonumber \\
&=& \arctan \left(\frac{k+1}{k+2}\right) \nonumber \\
&=& \text{RHS}.
\end{eqnarray}$$
Since $\text{P}_1$ is true and $\text{P}_k$ is true implies $\text{P}_{k+1}$ is also true, by the principle of mathematical induction, $\text{P}_n$ is true for $n\in\mathbb{Z}^+$.
Question
The diagram below shows the boundary of the cross-section of a water channel.
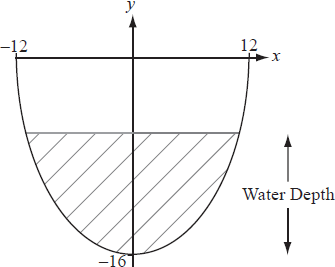
The equation that represents this boundary is \(y = 16\sec \left( {\frac{{\pi x}}{{36}}} \right) – 32\) where x and y are both measured in cm.
The top of the channel is level with the ground and has a width of 24 cm. The maximum depth of the channel is 16 cm.
Find the width of the water surface in the channel when the water depth is 10 cm.
Give your answer in the form \(a\arccos b\) where \(a,{\text{ }}b \in \mathbb{R}\) .
Answer/Explanation
Markscheme
10 cm water depth corresponds to \(16\sec \left( {\frac{{\pi x}}{{36}}} \right) – 32 = – 6\) (A1)
Rearranging to obtain an equation of the form \(\sec \left( {\frac{{\pi x}}{{36}}} \right) = k\) or equivalent
i.e. making a trignometrical function the subject of the equation. M1
\(\cos \left( {\frac{{\pi x}}{{36}}} \right) = \frac{8}{{13}}\) (A1)
\(\frac{{\pi x}}{{36}} = \pm \arccos \frac{8}{{13}}\) M1
\(x = \pm \frac{{36}}{\pi }\arccos \frac{8}{{13}}\) A1
Note: Do not penalise the omission of ±.
Width of water surface is \(\frac{{72}}{\pi }\arccos \frac{8}{{13}}{\text{ (cm)}}\) R1 N1
Note: Candidate who starts with 10 instead of −6 has the potential to gain the two M1 marks and the R1 mark.
[6 marks]
Question
(a) Show that \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right) = \frac{\pi }{4}\) .
(b) Hence, or otherwise, find the value of \(\arctan (2) + \arctan (3)\) .
Answer/Explanation
Markscheme
(a) METHOD 1
let \(x = \arctan \frac{1}{2} \Rightarrow \tan x = \frac{1}{2}\) and \(y = \arctan \frac{1}{3} \Rightarrow \tan y = \frac{1}{3}\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}} = 1\) M1
so, \(x + y = \arctan 1 = \frac{\pi }{4}\) A1AG
METHOD 2
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right)\) if \(xy < 1\) M1
so, \(\arctan \frac{1}{2} + \arctan \frac{1}{3} = \arctan \left( {\frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}}} \right) = \frac{\pi }{4}\) A1AG
METHOD 3
an appropriate sketch M1
e.g. 
correct reasoning leading to \(\frac{\pi }{4}\) R1AG
(b) METHOD 1
\(\arctan (2) + \arctan (3) = \frac{\pi }{2} – \arctan \left( {\frac{1}{2}} \right) + \frac{\pi }{2} – \arctan \left( {\frac{1}{3}} \right)\) (M1)
\( = \pi – \left( {\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right)} \right)\) (A1)
Note: Only one of the previous two marks may be implied.
\( = \pi – \frac{\pi }{4} = \frac{{3\pi }}{4}\) A1 N1
METHOD 2
let \(x = \arctan 2 \Rightarrow \tan x = 2\) and \(y = \arctan 3 \Rightarrow \tan y = 3\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{2 + 3}}{{1 – 2 \times 3}} = – 1\) (M1)
as \(\frac{\pi }{4} < x < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < x < \frac{\pi }{2}} \right)\)
and \(\frac{\pi }{4} < y < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < y < \frac{\pi }{2}} \right)\)
\(\frac{\pi }{2} < x + y < \pi \,\,\,\,\,{\text{(accept }}0 < x + y < \pi )\) (R1)
Note: Only one of the previous two marks may be implied.
so, \(x + y = \frac{{3\pi }}{4}\) A1 N1
METHOD 3
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right) + \pi {\text{ if }}xy > 1\) (M1)
so, \(\arctan 2 + \arctan 3 = \arctan \left( {\frac{{2 + 3}}{{1 – 2 \times 3}}} \right) + \pi \) (A1)
Note: Only one of the previous two marks may be implied.
\( = \frac{{3\pi }}{4}\) A1 N1
METHOD 4
an appropriate sketch M1
e.g. 
correct reasoning leading to \(\frac{{3\pi }}{4}\) R1A1
[5 marks]
Question
The first three terms of a geometric sequence are \(\sin x,{\text{ }}\sin 2x\) and \(4\sin x{\cos ^2}x,{\text{ }} – \frac{\pi }{2} < x < \frac{\pi }{2}\).
(a) Find the common ratio r.
(b) Find the set of values of x for which the geometric series \(\sin x + \sin 2x + 4\sin x{\cos ^2}x + \ldots \) converges.
Consider \(x = \arccos \left( {\frac{1}{4}} \right),{\text{ }}x > 0\).
(c) Show that the sum to infinity of this series is \(\frac{{\sqrt {15} }}{2}\).
Answer/Explanation
Markscheme
(a) \(\sin x,{\text{ }}\sin 2x{\text{ and }}4\sin x{\cos ^2}x\)
\(r = \frac{{2\sin x\cos x}}{{\sin x}} = 2\cos x\) A1
Note: Accept \(\frac{{\sin 2x}}{{\sin x}}\).
[1 mark]
(b) EITHER
\(\left| r \right| < 1 \Rightarrow \left| {2\cos x} \right| < 1\) M1
OR
\( – 1 < r < 1 \Rightarrow – 1 < 2\cos x < 1\) M1
THEN
\(0 < \cos x < \frac{1}{2}{\text{ for }} – \frac{\pi }{2} < x < \frac{\pi }{2}\)
\( – \frac{\pi }{2} < x < – \frac{\pi }{3}{\text{ or }}\frac{\pi }{3} < x < \frac{\pi }{2}\) A1A1
[3 marks]
(c) \({S_\infty } = \frac{{\sin x}}{{1 – 2\cos x}}\) M1
\({S_\infty } = \frac{{\sin \left( {\arccos \left( {\frac{1}{4}} \right)} \right)}}{{1 – 2\cos \left( {\arccos \left( {\frac{1}{4}} \right)} \right)}}\)
\( = \frac{{\frac{{\sqrt {15} }}{4}}}{{\frac{1}{2}}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
\( = \frac{{\sqrt {15} }}{2}\) AG
[3 marks]
Total [7 marks]
Question
Consider the following functions:
\(h(x) = \arctan (x),{\text{ }}x \in \mathbb{R}\)
\(g(x) = \frac{1}{x}\), \(x\in \mathbb{R}\), \({\text{ }}x \ne 0\)
Sketch the graph of \(y = h(x)\).[2]
Find an expression for the composite function \(h \circ g(x)\) and state its domain.[2]
Given that \(f(x) = h(x) + h \circ g(x)\),
(i) find \(f'(x)\) in simplified form;
(ii) show that \(f(x) = \frac{\pi }{2}\) for \(x > 0\).[7]
Nigel states that \(f\) is an odd function and Tom argues that \(f\) is an even function.
(i) State who is correct and justify your answer.
(ii) Hence find the value of \(f(x)\) for \(x < 0\).[3]
Answer/Explanation
Markscheme
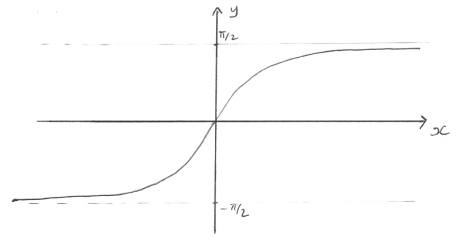 A1A1
A1A1
Note: A1 for correct shape, A1 for asymptotic behaviour at \(y = \pm \frac{\pi }{2}\).
[2 marks]
\(h \circ g(x) = \arctan \left( {\frac{1}{x}} \right)\) A1
domain of \(h \circ g\) is equal to the domain of \(g:x \in \circ ,{\text{ }}x \ne 0\) A1
[2 marks]
(i) \(f(x) = \arctan (x) + \arctan \left( {\frac{1}{x}} \right)\)
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{1}{{1 + \frac{1}{{{x^2}}}}} \times – \frac{1}{{{x^2}}}\) M1A1
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{{ – \frac{1}{{{x^2}}}}}{{\frac{{{x^2} + 1}}{{{x^2}}}}}\) (A1)
\( = \frac{1}{{1 + {x^2}}} – \frac{1}{{1 + {x^2}}}\)
\( = 0\) A1
(ii) METHOD 1
f is a constant R1
when \(x > 0\)
\(f(1) = \frac{\pi }{4} + \frac{\pi }{4}\) M1A1
\( = \frac{\pi }{2}\) AG
METHOD 2
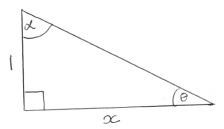
from diagram
\(\theta = \arctan \frac{1}{x}\) A1
\(\alpha = \arctan x\) A1
\(\theta + \alpha = \frac{\pi }{2}\) R1
hence \(f(x) = \frac{\pi }{2}\) AG
METHOD 3
\(\tan \left( {f(x)} \right) = \tan \left( {\arctan (x) + \arctan \left( {\frac{1}{x}} \right)} \right)\) M1
\( = \frac{{x + \frac{1}{x}}}{{1 – x\left( {\frac{1}{x}} \right)}}\) A1
denominator = 0, so \(f(x) = \frac{\pi }{2}{\text{ (for }}x > 0)\) R1
[7 marks]
(i) Nigel is correct. A1
METHOD 1
\(\arctan (x)\) is an odd function and \(\frac{1}{x}\) is an odd function
composition of two odd functions is an odd function and sum of two odd functions is an odd function R1
METHOD 2
\(f( – x) = \arctan ( – x) + \arctan \left( { – \frac{1}{x}} \right) = – \arctan (x) – \arctan \left( {\frac{1}{x}} \right) = – f(x)\)
therefore f is an odd function. R1
(ii) \(f(x) = – \frac{\pi }{2}\) A1
[3 marks]
Question
Write down the general solutions (in radians) for the equations
Answer/Explanation
Ans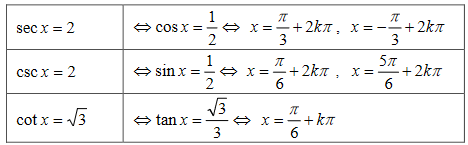
Question
Solve the equations
(a) \(cos(2arcsinx)=0.68\), by applying a double angle identity.
(b) arctan x + arctan 2x = arctan \(\sqrt{2}\), by applying tan(A+B)
Answer/Explanation
Ans
(a) \(1-2x^2=0.68 \Rightarrow … \Rightarrow x=0.4\) (b) \(\frac{2+2x}{1-2x^2}=\sqrt{2} \Rightarrow … \Rightarrow x=\frac{\sqrt{2}}{4}\)
Question
(a) Write down the domain and the range of the function f(x) = arctan x.
(b) By applying tan, find the values of
\(A=arctan\frac{1}{3}+arctan\frac{1}{2},\) \(B=arctan 2 + arctan 3\)
\(C=arctan\frac{1}{3}-arctan2\) \(D=arctan\frac{2}{3}+arctan\frac{3}{2}\)
Answer/Explanation
Ans
(a) x∈R, \(-\frac{\pi}{2}<y<\frac{\pi}{2}\)
(b) \(tan A = 1 \Rightarrow A=\frac{\pi}{4}\) \(tan B=-1 \Rightarrow B=\frac{3\pi}{4}\) (B is +tive)
\(tan C=-1\Rightarrow C=-\frac{\pi}{4}\), (C is -tive) tan D not defined \(\Rightarrow D=\frac{\pi}{2}\)Questions 23-25 : without GDC.
Question
Solve 2 sin x = tan x, where \(-\frac{\pi}{2}<x<\frac{\pi}{2}\).
Answer/Explanation
Ans
\(2sinx =tanx\)
\(\Rightarrow 2sinx cosx-sinx =0\)
\(\Rightarrow sin x(2cos x-1)=0\)
\(\Rightarrow sin x =0, cos x =\frac{1}{2}\)
\(\Rightarrow sin x = 0, x = \pm \frac{\pi}{3}\)
Question
Solve \(tan^22θ=1\), in the interval \(-\frac{\pi}{2}≤θ≤\frac{\pi}{2}\)
Answer/Explanation
Ans
\(tan^22\theta = 1\)
\(\Rightarrow tan 2\theta=\pm 1\)
\(\theta = \pm \frac{3\pi}{4},\pm \frac{\pi}{4}\)
\(\Rightarrow = \pm\frac{3\pi}{8},\pm\frac{\pi}{8}\) or \(\pm 1.18, \pm 0.393\)
Question
The angle θ satisfies the equation \(2tan^2\theta – 5sec\theta-10=0\), where θ is in the second qaudrant. Find the exact value of sec θ.
Extra question (by GDC)
(a) Solve the equation \(2 tan^2 \theta-5sec\theta-10=0\) in the interval \(-\pi<x\theta<\pi\), by using the values of sec θ found above.
Answer/Explanation
Ans
\(2tan^2\theta – 5sec\theta -10=0\)
Using \(1+tan^2\theta=sec^2\theta = sec^2\theta, \Rightarrow (sec^2\theta -1)-5sec\theta – 10=0\)
\(2sec^2\theta – 5sec\theta-12=0\)
Solving the equation eg (2sec θ + 3)(sec θ – 4) = 0
\(sec\theta=-\frac{3}{2}\) or secθ = 4
θ in second quadrant \(\Rightarrow secθ\) is negative = secθ =-\(\frac{3}{2}\)
Extra question
\(secθ=-\frac{3}{2}\Rightarrow cos θ=-\frac{2}{3} \Rightarrow θ=cos^{-1}(-\frac{2}{3})\) or \(θ=-cos^{-1}(\frac{1}{4})\)
\(secθ=4\Rightarrow cosθ=\frac{1}{4} \Rightarrow θ=cos^{-1}(\frac{1}{4})\) or \(θ=-cos^{-1}{4}\)
Question
A television screen, BC, of height one metre, is built into a wall. The bottom of the television screen at B is one metre above an observer’s eye level. The angles of elevation (AOC, AOB) from the observer’s eye at O to the top ad bottom of the television screen are α and β radians respectively. The horizontal distance from the observer’s eye to the wall containing the television screen is x metres. The observer’s angle of vision (BOC) is θ radius, as shown below.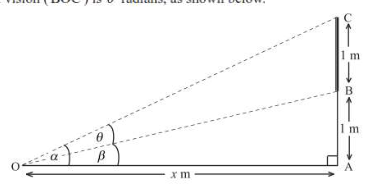
(a) show that = \(arctan\frac{2}{x}-arctan\frac{1}{x}\)
(b) Express θ in the form \(θ = arctan\frac{ax}{x^2+b}\), where a,b∈R
(c) Find the maximum value of angle θ, and teh value of x where this maximum occurs.
(d) Find where the observe should stand so that the angle of vision is 15o.
Answer/Explanation
Ans
Attempting to express α and β in terms of arctan
α = arctan\(\frac{2}{x}\) and \(β=arctan\frac{1}{x}\)
\(θ=arctan\frac{2}{x}-arctan\frac{1}{x}\)
(b) Using tan θ =\(\frac{tanα-tanβ}{1+tanαtanβ}\) to get tanθ in terms of x.
\(tan\Theta =\frac{\frac{2}{x}-\frac{1}{x}}{1+(\frac{2}{x})^2}(=\frac{x}{x^2+2})\)
θ=arctan \(\frac{x}{x^2+2}\)
(c) by GDC using graph x = 1.41 (in fact x = \(\sqrt{2}\))and θ = 0.340 radians
(d) METHOD 1
Attempting to solve \(arctan\frac{2}{x}-arctan\frac{1}{x}=15^o(=\frac{\pi}{112})\) fro x
x = 0.649, 3.08(m)
METHOD 2
Attempting to solve \(\frac{x}{x^2+2}=tan15^o\) (or equivalent) for x
x = 0.649, 3.08 (m)
