Question
Consider triangle ABC with \({\rm{B}}\hat {\rm{A}}{\rm{C}} = 37.8^\circ \) , AB = 8.75 and BC = 6 .
Find AC.
▶️Answer/Explanation
Markscheme
METHOD 1
Attempting to use the cosine rule i.e. \({\text{B}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{A}}{{\text{C}}^2} – 2 \times {\text{AB}} \times {\text{AC}} \times \cos {\rm{B\hat AC}}\) (M1)
\({6^2} = {8.75^2} + {\text{A}}{{\text{C}}^2} – 2 \times 8.75 \times {\text{AC}} \times \cos 37.8^\circ \) (or equivalent) A1
Attempting to solve the quadratic in AC e.g. graphically, numerically or with quadratic formula M1A1
Evidence from a sketch graph or their quadratic formula (AC = …) that there are two values of AC to determine. (A1)
AC = 9.60 or AC = 4.22 A1A1 N4
Note: Award (M1)A1M1A1(A0)A1A0 for one correct value of AC.
[7 marks]
METHOD 2
Attempting to use the sine rule i.e. \(\frac{{{\rm{BC}}}}{{\sin {\rm{B\hat AC}}}} = \frac{{{\rm{AB}}}}{{\sin {\rm{A\hat CB}}}}\) (M1)
\(\sin C = \frac{{8.75\sin 37.8^\circ }}{6}\,\,\,\,\,{\text{( = 0.8938…)}}\) (A1)
C = 63.3576…° A1
C = 116.6423…° and B = 78.842…° or B = 25.5576…° A1
EITHER
Attempting to solve \(\frac{{{\text{AC}}}}{{\sin 78.842…^\circ }} = \frac{6}{{\sin 37.8^\circ }}{\text{ or }}\frac{{{\text{AC}}}}{{\sin 25.5576…^\circ }} = \frac{6}{{\sin 37.8^\circ }}\) M1
OR
Attempting to solve \({\text{A}}{{\text{C}}^2} = {8.75^2} + {6^2} – 2 \times 8.75 \times 6 \times \cos 25.5576…^\circ {\text{ or}}\)
\({\text{A}}{{\text{C}}^2} = {8.75^2} + {6^2} – 2 \times {8.75^2} \times 6 \times \cos 78.842…^\circ \) M1
\({\text{AC}} = 9.60{\text{ or AC}} = 4.22\) A1A1 N4
Note: Award (M1)(A1)A1A0M1A1A0 for one correct value of AC.
[7 marks]
Examiners report
A large proportion of candidates did not identify the ambiguous case and hence they only obtained one correct value of AC. A number of candidates prematurely rounded intermediate results (angles) causing inaccurate final answers.
Question
In a triangle ABC, \(\hat A = 35^\circ \), BC = 4 cm and AC = 6.5 cm. Find the possible values of \(\hat B\) and the corresponding values of AB.
▶️Answer/Explanation
Markscheme
\(\frac{{\sin B}}{{6.5}} = \frac{{\sin 35^\circ }}{4}\) M1
\(\hat B = 68.8^\circ {\text{ or }}111^\circ \) A1A1
\(\hat C = 76.2^\circ \) or \(33.8^\circ \) (accept \(34^\circ \)) A1
\(\frac{{{\text{AB}}}}{{\sin C}} = \frac{{{\text{BC}}}}{{\sin A}}\)
\(\frac{{{\text{AB}}}}{{\sin 76.2^\circ }} = \frac{4}{{\sin 35^\circ }}\) (M1)
AB = 6.77 cm A1
\(\frac{{{\text{AB}}}}{{\sin 33.8^\circ }} = \frac{4}{{\sin 35^\circ }}\)
AB = 3.88 cm\(\,\,\,\,\,\)(accept 3.90) A1
[7 marks]
Examiners report
Most candidates realised that the sine rule was the best option although some used the more difficult cosine rule which was an alternative method. Many candidates failed to realise that there were two solutions even though the question suggested this. Many candidates were given an arithmetic penalty for giving one of the possible of values \({\hat B}\) as 112.2° instead of 111°.
Question
Consider the triangle ABC where \({\rm{B\hat AC}} = 70^\circ \), AB = 8 cm and AC = 7 cm. The point D on the side BC is such that \(\frac{{{\text{BD}}}}{{{\text{DC}}}} = 2\).
Determine the length of AD.
▶️Answer/Explanation
Markscheme
use of cosine rule: \({\text{BC}} = \sqrt {({8^2} + {7^2} – 2 \times 7 \times 8\cos 70)} = 8.6426 \ldots \) (M1)A1
Note: Accept an expression for \({\text{B}}{{\text{C}}^2}\).
\({\text{BD}} = 5.7617 \ldots \,\,\,\,\,{\text{(CD}} = 2.88085 \ldots )\) A1
use of sine rule: \(\hat B = \arcsin \left( {\frac{{7\sin 70}}{{{\text{BC}}}}} \right) = 49.561 \ldots ^\circ \,\,\,\,\,(\hat C = 60.4387 \ldots ^\circ )\) (M1)A1
use of cosine rule: \({\text{AD}} = \sqrt {{8^2} + {\text{B}}{{\text{D}}^2} – 2 \times {\text{BD}} \times 8\cos B} = 6.12{\text{ (cm)}}\) A1
Note: Scale drawing method not acceptable.
[6 marks]
Examiners report
Well done.
Question
A triangle \(ABC\) has \(\hat A = 50^\circ \), \({\text{AB}} = 7{\text{ cm}}\) and \({\text{BC}} = 6{\text{ cm}}\). Find the area of the triangle given that it is smaller than \(10{\text{ c}}{{\text{m}}^2}\).
▶️Answer/Explanation
Markscheme
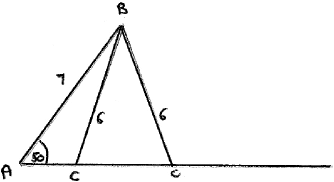
METHOD 1
\(\frac{6}{{\sin 50}} = \frac{7}{{\sin C}} \Rightarrow \sin C = \frac{{7\sin 50}}{6}\) (M1)
\(C = 63.344 \ldots \) (A1)
or\(\;\;\;C = 116.655 \ldots \) (A1)
\(B = 13.344 \ldots \;\;\;({\text{or }}B = 66.656 \ldots )\) (A1)
\({\text{area}} = \frac{1}{2} \times 6 \times 7 \times \sin 13.344 \ldots \;\;\;\left( {{\text{or }}\frac{1}{2} \times 6 \times 7 \times \sin 66.656 \ldots } \right)\) (M1)
\(4.846 \ldots \;\;\;({\text{or }} = 19.281 \ldots )\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 2
\({6^2} = {7^2} + {b^2} – 2 \times 7b\cos 50\) (M1)(A1)
\({b^2} – 14b\cos 50 + 13 = 0\;\;\;\)or equivalent method to solve the above equation (M1)
\(b = 7.1912821 \ldots \;\;\;{\text{or}}\;\;\;b = 1.807744 \ldots \) (A1)
\({\text{area}} = \frac{1}{2} \times 7 \times 1.8077 \ldots \sin 50 = 4.846 \ldots \) (M1)
\(\left( {{\text{or }}\frac{1}{2} \times 7 \times 7.1912821 \ldots \sin 50 = 19.281 \ldots } \right)\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 3
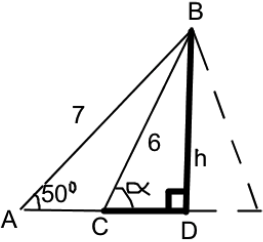
Diagram showing triangles \(ACB\) and \(ADB\) (M1)
\(h = 7\sin (50) = 5.3623 \ldots {\text{ (cm)}}\) (M1)
\(\alpha = \arcsin \frac{h}{6} = 63.3442 \ldots \) (M1)
\({\text{AC}} = {\text{AD}} – {\text{CD}} = 7\cos 50 – 6\cos \alpha = 1.8077 \ldots {\text{ (cm)}}\) (M1)
\({\text{area}} = \frac{1}{2} \times 1.8077 \ldots \times 5.3623 \ldots \) (M1)
\( = 4.85{\text{ (c}}{{\text{m}}^{\text{2}}}{\text{)}}\) A1
Total [6 marks]
Examiners report
Most candidates scored 4/6 showing that candidates do not have enough experience with the ambiguous case. Very few candidates drew a suitable diagram that would have illustrated this fact which could have helped them to understand the requirement that the answer should be less than 10. In fact many candidates ignored this requirement or used it incorrectly to solve an inequality.
Question
ABCD is a quadrilateral where \({\text{AB}} = 6.5,{\text{ BC}} = 9.1,{\text{ CD}} = 10.4,{\text{ DA}} = 7.8\) and \({\rm{C\hat DA}} = 90^\circ \). Find \({\rm{A\hat BC}}\), giving your answer correct to the nearest degree.
▶️Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {7.8^2} + {10.4^2}\) (M1)
\({\text{AC}} = 13\) (A1)
use of cosine rule eg, \(\cos ({\rm{A\hat BC}}) = \frac{{{{6.5}^2} + {{9.1}^2} – {{13}^2}}}{{2(6.5)(9.1)}}\) M1
\({\rm{A\hat BC}} = 111.804 \ldots ^\circ {\text{ }}( = 1.95134 \ldots )\) (A1)
\( = 112^\circ \) A1
[5 marks]
Examiners report
Well done by most candidates. A small number of candidates did not express the required angle correct to the nearest degree.
Question
In a triangle \({\text{ABC, AB}} = 4{\text{ cm, BC}} = 3{\text{ cm}}\) and \({\rm{B\hat AC}} = \frac{\pi }{9}\).
a.Use the cosine rule to find the two possible values for AC.[5]
b.Find the difference between the areas of the two possible triangles ABC.[3]
▶️Answer/Explanation
Markscheme
METHOD 1
let \({\text{AC}} = x\)
\({3^2} = {x^2} + {4^2} – 8x\cos \frac{\pi }{9}\) M1A1
attempting to solve for \(x\) (M1)
\(x = 1.09,{\text{ }}6.43\) A1A1
METHOD 2
let \({\text{AC}} = x\)
using the sine rule to find a value of \(C\) M1
\({4^2} = {x^2} + {3^2} – 6x\cos (152.869 \ldots ^\circ ) \Rightarrow x = 1.09\) (M1)A1
\({4^2} = {x^2} + {3^2} – 6x\cos (27.131 \ldots ^\circ ) \Rightarrow x = 6.43\) (M1)A1
METHOD 3
let \({\text{AC}} = x\)
using the sine rule to find a value of \(B\) and a value of \(C\) M1
obtaining \(B = 132.869 \ldots ^\circ ,{\text{ }}7.131 \ldots ^\circ \) and \(C = 27.131 \ldots ^\circ ,{\text{ }}152.869 \ldots ^\circ \) A1
\((B = 2.319 \ldots ,{\text{ }}0.124 \ldots \) and \(C = 0.473 \ldots ,{\text{ }}2.668 \ldots )\)
attempting to find a value of \(x\) using the cosine rule (M1)
\(x = 1.09,{\text{ }}6.43\) A1A1
Note: Award M1A0(M1)A1A0 for one correct value of \(x\)
[5 marks]
\(\frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9}\) and \(\frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}\) (A1)
(\(4.39747 \ldots \) and \(0.744833 \ldots \))
let \(D\) be the difference between the two areas
\(D = \frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9} – \frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}\) (M1)
\((D = 4.39747 \ldots – 0.744833 \ldots )\)
\( = 3.65{\text{ (c}}{{\text{m}}^2})\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” \((S)\) is at an angle of depression of 25°.
“Nauti Buoy” \((N)\) is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle \({\text{SXN}} = \) 70°.
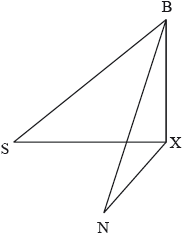
Find, to 3 significant figures, the distance between the two yachts.
▶️Answer/Explanation
Markscheme
attempt to use tan, or sine rule, in triangle BXN or BXS (M1)
\({\text{NX}} = 80\tan 55{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 35{\rm{^\circ }}}} = 114.25} \right)\) (A1)
\({\text{SX}} = 80\tan 65{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 25{\rm{^\circ }}}} = 171.56} \right)\) (A1)
Attempt to use cosine rule M1
\({\text{S}}{{\text{N}}^2} = {171.56^2} + {114.25^2} – 2 \times 171.56 \times 114.25\cos 70\)° (A1)
\({\text{SN}} = 171{\text{ }}({\text{m}})\) A1
Note: Award final A1 only if the correct answer has been given to 3 significant figures.
[6 marks]
Examiners report
Question
A ship, S, is 10 km north of a motorboat, M, at 12.00pm. The ship is travelling northeast with a constant velocity of \(20{\text{ km}}\,{\text{h}}{{\text{r}}^{ – 1}}\). The motorboat wishes to intercept the ship and it moves with a constant velocity of \(30{\text{ km}}\,{\text{h}}{{\text{r}}^{ – 1}}\) in a direction \(\theta \) degrees east of north. In order for the interception to take place, determine
a.the value of \(\theta \).[4]
b.the time at which the interception occurs, correct to the nearest minute.[5]
▶️Answer/Explanation
Markscheme
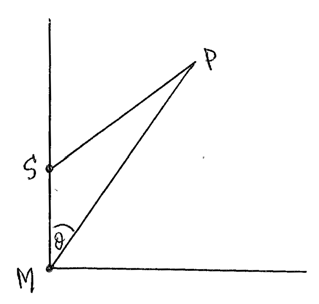
let the interception occur at the point P, t hrs after 12:00
then, SP = 20t and MP = 30t A1
using the sine rule,
\(\frac{{{\text{SP}}}}{{{\text{MP}}}} = \frac{2}{3} = \frac{{\sin \theta }}{{\sin 135}}\) M1A1
whence \(\theta = 28.1\) A1
[4 marks]
using the sine rule again,
\(\frac{{{\text{MP}}}}{{{\text{MS}}}} = \frac{{\sin 135}}{{\sin (45 – 28.1255 \ldots )}}\) M1A1
\(30t = 10 \times \frac{{\sin 135}}{{\sin 16.8745 \ldots }}\) M1
\(t = 0.81199 \ldots \) A1
the interception occurs at 12:49 A1
[5 marks]
Examiners report
[N/A]
[N/A]
Question
A ship, S, is 10 km north of a motorboat, M, at 12.00pm. The ship is travelling northeast with a constant velocity of \(20{\text{ km}}\,{\text{h}}{{\text{r}}^{ – 1}}\). The motorboat wishes to intercept the ship and it moves with a constant velocity of \(30{\text{ km}}\,{\text{h}}{{\text{r}}^{ – 1}}\) in a direction \(\theta \) degrees east of north. In order for the interception to take place, determine
a.the value of \(\theta \).[4]
b.the time at which the interception occurs, correct to the nearest minute.[5]
▶️Answer/Explanation
Markscheme
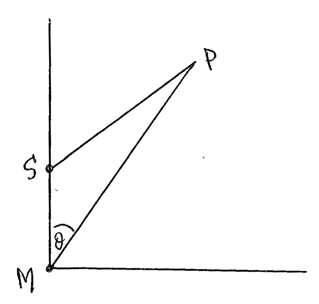
let the interception occur at the point P, t hrs after 12:00
then, SP = 20t and MP = 30t A1
using the sine rule,
\(\frac{{{\text{SP}}}}{{{\text{MP}}}} = \frac{2}{3} = \frac{{\sin \theta }}{{\sin 135}}\) M1A1
whence \(\theta = 28.1\) A1
[4 marks]
using the sine rule again,
\(\frac{{{\text{MP}}}}{{{\text{MS}}}} = \frac{{\sin 135}}{{\sin (45 – 28.1255 \ldots )}}\) M1A1
\(30t = 10 \times \frac{{\sin 135}}{{\sin 16.8745 \ldots }}\) M1
\(t = 0.81199 \ldots \) A1
the interception occurs at 12:49 A1
[5 marks]
