Question
Consider the vectors a \( = \sin (2\alpha )\)i \( – \cos (2\alpha )\)j + k and b \( = \cos \alpha \)i \( – \sin \alpha \)j − k, where \(0 < \alpha < 2\pi \).
Let \(\theta \) be the angle between the vectors a and b.
(a) Express \(\cos \theta \) in terms of \(\alpha \).
(b) Find the acute angle \(\alpha \) for which the two vectors are perpendicular.
(c) For \(\alpha = \frac{{7\pi }}{6}\), determine the vector product of a and b and comment on the geometrical significance of this result.
▶️Answer/Explanation
Markscheme
(a) \(\cos \theta = \frac{{\boldsymbol{ab}}}{{\left| \boldsymbol{a} \right|\left| \boldsymbol{b} \right|}} = \frac{{\sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha – 1}}{{\sqrt 2 \times \sqrt 2 }}{\text{ }}\left( { = \frac{{\sin 3\alpha – 1}}{2}} \right)\) M1A1
(b) \({\boldsymbol{a}} \bot {\boldsymbol{b}} \Rightarrow \cos \theta = 0\) M1
\(\sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha – 1 = 0\)
\(\alpha = 0.524{\text{ }}\left( { = \frac{\pi }{6}} \right)\) A1
(c)
METHOD 1
\(\left| {\begin{array}{*{20}{c}}
{\boldsymbol{i}}&{\boldsymbol{j}}&{\boldsymbol{k}} \\
{\sin 2\alpha }&{ – \cos 2\alpha }&1 \\
{\cos \alpha }&{ – \sin \alpha }&{ – 1}
\end{array}} \right|\) (M1)
assuming \(\alpha = \frac{{7\pi }}{6}\)
Note: Allow substitution at any stage.
\(\left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\
{\frac{{\sqrt 3 }}{2}}&{ – \frac{1}{2}}&1 \\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}&{ – 1}
\end{array}} \right|\) A1
\(= \boldsymbol{i} \left( {\frac{1}{2} – \frac{1}{2}} \right) – \boldsymbol{j} \left( { – \frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{2}} \right) + \boldsymbol{k}\left( {\frac{{\sqrt 3 }}{2} \times \frac{1}{2} – \frac{1}{2} \times \frac{{\sqrt 3 }}{2}} \right)\)
= 0 A1
a and b are parallel R1
Note: Accept decimal equivalents.
METHOD 2
from (a) \(\cos \theta = – 1{\text{ (and }}\sin \theta = 0)\) M1A1
\(\boldsymbol{a} \times \boldsymbol{b}\) = 0 A1
a and b are parallel R1
[8 marks]
Examiners report
This question was attempted by most candidates who in general were able to find the dot product of the vectors in part (a). However the simplification of the expression caused difficulties which affected the performance in part (b). Many candidates had difficulties in interpreting the meaning of a \( \times \) b = 0 in part (c).
Question
The diagram shows a cube OABCDEFG.
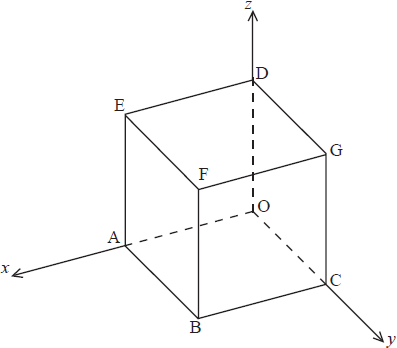
Let O be the origin, (OA) the x-axis, (OC) the y-axis and (OD) the z-axis.
Let M, N and P be the midpoints of [FG], [DG] and [CG], respectively.
The coordinates of F are (2, 2, 2).
(a) Find the position vectors \(\overrightarrow {{\text{OM}}} \), \(\overrightarrow {{\text{ON}}} \) and \(\overrightarrow {{\text{OP}}} \) in component form.
(b) Find \(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} \).
(c) Hence,
(i) calculate the area of the triangle MNP;
(ii) show that the line (AG) is perpendicular to the plane MNP;
(iii) find the equation of the plane MNP.
(d) Determine the coordinates of the point where the line (AG) meets the plane MNP.
▶️Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{OM}}} = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right)\), \(\overrightarrow {{\text{ON}}} = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
2
\end{array}} \right)\) and \(\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
1
\end{array}} \right)\) A1A1A1
[3 marks]
(b) \(\overrightarrow {{\text{MP}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
0 \\
{ – 1}
\end{array}} \right)\) and \(\overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
0
\end{array}} \right)\) A1A1
\(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&0&{ – 1} \\
{ – 1}&{ – 1}&0
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) (M1)A1
[4 marks]
(c) (i) area of MNP \( = \frac{1}{2}\left| {\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} } \right|\) M1
\( = \frac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)} \right|\)
\( = \frac{{\sqrt 3 }}{2}\) A1
(ii) \(\overrightarrow {{\text{OA}}} = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right)\), \(\overrightarrow {{\text{OG}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
2
\end{array}} \right)\)
\(\overrightarrow {{\text{AG}}} = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
since \(\overrightarrow {{\text{AG}}} = 2(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} )\) AG is perpendicular to MNP R1
(iii) \(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) M1A1
\(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) (accept \( – x + y + z = 3\)) A1
[7 marks]
(d) \(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
\(\left( {\begin{array}{*{20}{c}}
{2 – 2\lambda } \\
{2\lambda } \\
{2\lambda }
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) M1A1
\( – 2 + 2\lambda + 2\lambda + 2\lambda = 3\)
\(\lambda = \frac{5}{6}\) A1
\(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \frac{5}{6}\left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) M1
coordinates of point \(\left( {\frac{1}{3},\frac{5}{3},\frac{5}{3}} \right)\) A1
[6 marks]
Total [20 marks]
Examiners report
This was the most successfully answered question in part B, with many candidates achieving full marks. There were a few candidates who misread the question and treated the cube as a unit cube. The most common errors were either algebraic or arithmetic mistakes. A variety of notation forms were seen but in general were used consistently. In a few cases, candidates failed to show all the work or set it properly.
Question
The points A and B have position vectors \(\overrightarrow {{\text{OA}}} = \left\{ {\begin{array}{*{20}{c}} 1 \\ 2 \\ { – 2} \end{array}} \right\}\) and \(\overrightarrow {{\text{OB}}} = \left\{ {\begin{array}{*{20}{c}} 1 \\ 0 \\ 2 \end{array}} \right\}\).
a.Find \(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} \).[2]
b.Hence find the area of the triangle OAB.[2]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} = \left( {\begin{array}{*{20}{c}} 4 \\ { – 4} \\ { – 2} \end{array}} \right)\) (M1)A1
Note: M1A0 can be awarded for attempt at a correct method shown, or correct method implied by the digits 4, 4, 2 found in the correct order.
[2 marks]
\({\text{area}} = \frac{1}{2}\sqrt {{4^2} + {4^2} + {2^2}} = 3\) M1A1
[2 marks]
Question
The points A and B have coordinates (1, 2, 3) and (3, 1, 2) relative to an origin O.
a.(i) Find \(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} \) .
(ii) Determine the area of the triangle OAB.
(iii) Find the Cartesian equation of the plane OAB.[5]
(ii) The line \({L_2}\) has vector equation \(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2 \\
4 \\
3
\end{array}} \right) + \mu \left( {\begin{array}{*{20}{c}}
1 \\
3 \\
2
\end{array}} \right)\).
Determine whether or not \({L_1}\) and \({L_2}\) are skew.[7]
▶️Answer/Explanation
Markscheme
(i) \(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} = \) i + 7j – 5k A1
(ii) area \( = \frac{1}{2}|\)i + 7j – 5k\(| = \frac{{5\sqrt 3 }}{2}{\text{(4.33)}}\) M1A1
(iii) equation of plane is \(x + 7y – 5z = k\) M1
\(x + 7y – 5z = 0\) A1
[5 marks]
(i) direction of line = (3i + j + 2k) – (i + 2j + 3k) = 2i – j – k M1A1
equation of line is
r = (i + 2j + 3k) + \(\lambda \)(2i – j – k) A1
(ii) at a point of intersection,
\(1 + 2\lambda = 2 + \mu \)
\(2 – \lambda = 4 + 3\mu \) M1A1
\(3 – \lambda = 3 + 2\mu \)
solving the \({2^{{\text{nd}}}}\) and \({3^{{\text{rd}}}}\) equations, \(\lambda = 4{\text{, }}\mu = – 2\) A1
these values do not satisfy the \({1^{{\text{st}}}}\) equation so the lines are skew R1
[7 marks]
Question
The function f is defined on the domain [0, 2] by \(f(x) = \ln (x + 1)\sin (\pi x)\) .
a.Obtain an expression for \(f'(x)\) .[3]
b.Sketch the graphs of f and \(f’\) on the same axes, showing clearly all x-intercepts.[4]
c.Find the x-coordinates of the two points of inflexion on the graph of f .[2]
d.Find the equation of the normal to the graph of f where x = 0.75 , giving your answer in the form y = mx + c .[3]
e.Consider the points \({\text{A}}\left( {a{\text{ }},{\text{ }}f(a)} \right)\) , \({\text{B}}\left( {b{\text{ }},{\text{ }}f(b)} \right)\) and \({\text{C}}\left( {c{\text{ }},{\text{ }}f(c)} \right)\) where a , b and c \((a < b < c)\) are the solutions of the equation \(f(x) = f'(x)\) . Find the area of the triangle ABC.[6]
▶️Answer/Explanation
Markscheme
\(f'(x) = \frac{1}{{x + 1}}\sin (\pi x) + \pi \ln (x + 1)\cos (\pi x)\) M1A1A1
[3 marks]
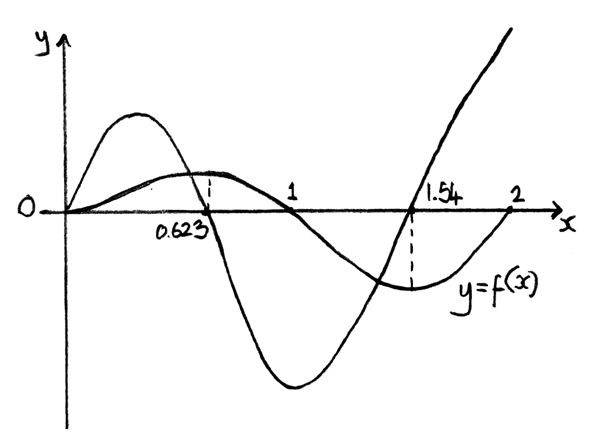 A4
A4
Note: Award A1A1 for graphs, A1A1 for intercepts.
[4 marks]
0.310, 1.12 A1A1
[2 marks]
\(f'(0.75) = – 0.839092\) A1
so equation of normal is \(y – 0.39570812 = \frac{1}{{0.839092}}(x – 0.75)\) M1
\(y = 1.19x – 0.498\) A1
[3 marks]
\({\text{A}}(0,{\text{ }}0)\)
\({\text{B(}}\overbrace {0.548 \ldots }^c,\overbrace {0.432 \ldots }^d)\) A1
\({\text{C(}}\overbrace {1.44 \ldots }^e,\overbrace { – 0.881 \ldots }^f)\) A1
Note: Accept coordinates for B and C rounded to 3 significant figures.
area \(\Delta {\text{ABC}} = \frac{1}{2}|\)(ci + dj) \( \times \) (ei + fj)\(|\) M1A1
\( = \frac{1}{2}(de – cf)\) A1
\( = 0.554\) A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
