Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 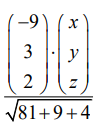
\(=\frac{32}{\sqrt{94}}\)

Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 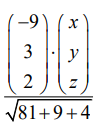
\(=\frac{32}{\sqrt{94}}\)

Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 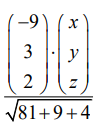
\(=\frac{32}{\sqrt{94}}\)

Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]
b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ.[2]
▶️Answer/Explanation
Markscheme
a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.
[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.
[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1
[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
- If \(u = i +2j + 3k\) and \(v = 2i – j + 2k\), show that \(u × v = 7i + 4j – 5k\).
- Let \(w = \lambda u +\mu v\) where \(\lambda\) and \(\mu\) are scalars. Show that \(w\) is perpendicular to the line of intersection of the planes \(x + 2y + 3z = 5\) and \(2x – y + 2z = 7\) for all values of \(\lambda\) and \(\mu\).
▶️Answer/Explanation
Ans:
- \(u × v = \begin{vmatrix} i & j & k\\ 1 & 2 & 3\\ 2 & -1 & 2 \end{vmatrix}=i \begin{vmatrix} 2 & 3 \\ -1 & 2 \end{vmatrix} – j \begin{vmatrix} 1 & 3 \\ 2 & 2 \end{vmatrix}+k \begin{vmatrix} 1 & 2 \\ 2 & -1 \end{vmatrix}\)
- \(w= \begin{pmatrix} \lambda+2\mu \\ 2\lambda-\mu \\ 3\lambda+2\mu \end{pmatrix}\)
The line of intersection of the planes is parallel to \(u × v\).
Now, \(w . (u × v) = 7\lambda + 14\mu + 8\lambda – 4\mu –15\lambda – 10\mu = 0 for all \lambda, \mu\).
Therefore, \(w\) is perpendicular to the line of intersection of the given planes.
OR
The line of intersection of the planes is perpendicular to \(u\) and to \(v\),
so it will be perpendicular to the plane containing \(u\) and \(v\), that is,
to all vectors of the form \(\lambda u + \mu v = w\).
Question
A ray of light coming from the point \((−1, 3, 2)\) is travelling in the direction of vector \(\begin{pmatrix} 4 \\ 1 \\ -2 \end{pmatrix}\) and meets the plane \(\pi: x + 3y + 2z − 24 = 0\). Find the angle that the ray of light makes with the plane.
▶️Answer/Explanation
Ans:
The normal vector to the plane is \(\begin{pmatrix} 1\\ 3\\ 2 \end{pmatrix}\)
EITHER \(\theta\) is the angle between the line and the normal to the plane.
\(cos \theta = \frac{\begin{pmatrix} 4 \\ 1 \\ -2 \end{pmatrix}.\begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix}}{\sqrt{14}\sqrt{21}} = \frac{3}{\sqrt{14}\sqrt{21}} \left ( =\frac{3}{7\sqrt{6}} \right )\)
⇒\(\theta=79.9\)° (=1.394…)
The required angle is 10.1° (= 0.176)
OR \(\phi\) is the angle between the line and the plane.
\(sin \phi = \frac{3}{\sqrt{14}\sqrt{21}}\)⇒\(\phi=\)10.1°(= 0.176)
Question
The line \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z+1}{2}\) is reflected in the plane \(x+y+z=1\). Calculate the angle between the line and its reflection. Give your answer in radians.
▶️Answer/Explanation
Ans:
Line direction is \(\begin{pmatrix} 1\\ 2 \\ 2 \end{pmatrix}\) and plane normal is \(\begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}\)
Angle \(\theta\) between these two given by
\(cos \theta = \frac{\begin{pmatrix} 1\\ 2 \\ 2 \end{pmatrix}.\begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}}{\sqrt{1^2+2^2+2^2}\sqrt{1^2+1^2+1^2}}\)
\(=\frac{5}{3\sqrt{3}}\)
\(\theta = arccos \frac{5}{3\sqrt{3}}\)
\(\theta = 0.276 radians\)
Angle between line and plane is \(\frac{\pi}{2}-0.276=1.295 radians\)
Angle between line and its reflection is \(1.295 × 2 = 2.59 radians\)
Note: Do not award the final (A1) if the answer is given in degrees, 148°.
Question
The line \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z+1}{2}\) is reflected in the plane \(x+y+z=1\). Calculate the angle between the line and its reflection. Give your answer in radians.
▶️Answer/Explanation
Ans:
Line direction is \(\begin{pmatrix} 1\\ 2 \\ 2 \end{pmatrix}\) and plane normal is \(\begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}\)
Angle \(\theta\) between these two given by
\(cos \theta = \frac{\begin{pmatrix} 1\\ 2 \\ 2 \end{pmatrix}.\begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}}{\sqrt{1^2+2^2+2^2}\sqrt{1^2+1^2+1^2}}\)
\(=\frac{5}{3\sqrt{3}}\)
\(\theta = arccos \frac{5}{3\sqrt{3}}\)
\(\theta = 0.276 radians\)
Angle between line and plane is \(\frac{\pi}{2}-0.276=1.295 radians\)
Angle between line and its reflection is \(1.295 × 2 = 2.59 radians\)
Note: Do not award the final (A1) if the answer is given in degrees, 148°.
Question
Find the cosine of the angle \(\theta\) between the planes \(\pi _1\) and \(\pi _2\) , where \(\pi _1\) has equation \(-2x+y-z=2\) and \(\pi _2\) has equation \(x+2y-z=6\) .
▶️Answer/Explanation
Ans:
\(n_1=-2i+j-k\) and \(n_2=i+2j-k\)
\(|n_1|=\sqrt{6}\) and \(|n_2|=\sqrt{6}\)
\(cos \theta = \frac{n_1.n_2}{|n_1||n_2|}\)
\(cos \theta = \frac{(-2i+j-k).(i+2j-k)}{\sqrt{6} × \sqrt{6}}\)
\(cos \theta = \frac{1}{6}\) (0.167 to 3 s.f.)
Question
Find the angle between the plane \(3x – 2y + 4z = 12\) and the \(z\)-axis. Give your answer to the nearest degree.
▶️Answer/Explanation
Ans:
\(z\)-axis has direction vector \(\begin{pmatrix} 0\\ 0\\ 1\end{pmatrix}\)
Let \(\theta\) equal the angle between the line and the normal to the plane.
\(cos \theta = \frac{\begin{pmatrix} 0\\ 0\\ 1\end{pmatrix}.\begin{pmatrix} 3\\ -2\\ 4\end{pmatrix}}{1\sqrt{3^2+2^2+4^2}}=\frac{4}{\sqrt{29}} \)
\(\theta=42\)°
The angle between the line and the plane is (90° – \(\theta\)).
The angle is 48°.
Question
Consider the point \(A(1, −1, 4)\) and the line \(L_2\) with equation \(r = 2i + 4j + 7k + t(2i + j + 3k),\) where \(t\)∈ \(R\) . Find the Cartesian equation of the plane that contains both the line \(L_2\) and point \(A\).
▶️Answer/Explanation
Ans:
The point (2, 4, 7) lies on the plane.
The vector joining (2, 4, 7) and (1, − 1, 4) and \(2i + j + 3k\) are parallel to the plane. So they are perpendicular to the normal to the plane.
\((i − j + 4k) − (2i + 4j + 7k) = − i − 5j − 3k \)
\(n=\begin{vmatrix} i & j & k\\ -1 & -5 & -3\\ 2 & 1 & 3 \end{vmatrix}= − 12i − 3j + 9k\) or equivalent parallel vector.
\(r • n = (i − j + 4k) • (−12i − 3j + 9k) = 27\)
Cartesian equation of plane is \(4x + y − 3z = −9\) (or equivalent)
Note: They can also use the form \(r=\begin{pmatrix} 1\\ -1\\ 4\end{pmatrix}+\lambda \begin{pmatrix} 2\\ 1\\ 3\end{pmatrix}+\mu \begin{pmatrix} -3\\ 3\\ -3\end{pmatrix}\) and eliminate the parameters \(\lambda\) ,\(\mu\).
Question
Find an equation of the plane containing the two lines \(x-1=\frac{1-y}{2}=z-2\) and \(\frac{x+1}{3}=\frac{2-y}{3}=\frac{z+2}{5}\).
▶️Answer/Explanation
Ans:
Let \(d_1\) and \(d_2\) be the direction vectors of the two lines. Then the normal to the plane is
\(d_1 × d_2= \begin{vmatrix} i & j & k\\ 1 & -2 & 1\\ 3 & -3 & 5 \end{vmatrix} = –7i – 2j + 3k\) (or equivalent)
Then equation of the plane is for the form \(–7x – 2y + 3z = c\)
Using the point (1, 1, 2) which is in the plane gives the equation of the plane \(–7x – 2y + 3z = –3\)
or \(r=\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}+\lambda \begin{pmatrix} 1\\ -2\\ 1\end{pmatrix}+\mu \begin{pmatrix} 3\\ -3\\ 5\end{pmatrix}\)
Question
A plane \(Π\) has equation \(r.\begin{pmatrix} 2\\ -1\\ 1\end{pmatrix}=16\) and line \(l\) has equations \(\frac{x-4}{-1}=\frac{y+2}{2}=\frac{z-6}{4}\). Show that the line \(l\) lies in the plane.
▶️Answer/Explanation
Ans:
The parametric equations of the line are
\(x=4-\lambda\)
\(y=-2+2\lambda\)
\(z=6+4\lambda\)
Substituting into the left hand side of the equation of the plane
\(2(4-\lambda)-(-2+2\lambda)+(6+4\lambda)\)=\(8-2\lambda+2-2\lambda+6+4\lambda\)=16
This equals the right hand side.
Hence the line is contained in the plane.
OR
We first need to prove that the line and the plane are parallel.
If true, the scalar product is zero.
\(\begin{pmatrix} -1\\ 2\\ 4\end{pmatrix}.\begin{pmatrix} 2\\ -1\\ 1\end{pmatrix}=-2-2+4=0\)
Now we need to show that a point on the line lies in the plane.
A point on the line is \((4,-2,6)\)
\(8+2+6=16\)
Hence this is true.
Therefore the line is contained in the plane.
Question
The plane \(6x – 2y + z = 11\) contains the line \(x-1=\frac{y+1}{2}=\frac{z-3}{l}\). Find \(l\).
▶️Answer/Explanation
Ans:
The direction vector, \(i + 2j + lk\), for the line, is perpendicular to \(6i – 2j + k\), the normal of the plane.
Therefore, \((i + 2j +lk) . (6i – 2j + k) = 0\)
Therefore, \(6 – 4 + l = 0\) so \(l = -2\)
OR
\(x = t + 1, y = 2t – 1, z = lt + 3\)
\(6t + 6 – 4t + 2 + lt + 3\)
\(2t + lt = 0\), so \(l = –2\)
Question
Find the coordinates of the point where the line given by the parametric equations \(x = 2\lambda + 4, y = –\lambda – 2, z = 3\lambda + 2\), intersects the plane with equation \(2x + 3y – z = 2. \)
▶️Answer/Explanation
Ans:
Substituting gives,
\(2(2\lambda + 4) + 3(–\lambda – 2) – (3\lambda + 2) = 2\)
⇔ \(4\lambda + 8 – 3\lambda – 6 – 3\lambda – 2 = 2\)
⇔ \(–2\lambda = 2\) ⇔ \(\lambda = –1\)
Intersection is \((2, –1, –1)\)
Question
Find the coordinates of the point of intersection of the line \(L\) with the plane \(P\) where: \(L: \frac{x+3}{2}=\frac{y-1}{-1}=\frac{z-1}{2}\) \(P: 2x+3y-z=-5\).
▶️Answer/Explanation
Ans:
Let \(\frac{x+3}{2}=\frac{y-1}{-1}=\frac{z-1}{2}=\lambda,\) then \(x=2\lambda-3,y=-\lambda+1,z=2\lambda+1\)
Substituting into P gives;
\(4\lambda – 6 – 3\lambda + 3 – 2\lambda – 1 = –5\)⇒ \(\lambda = 1\)
Therefore \(x = –1, y = 0, z = 3\)
Therefore the point of intersection is \((–1, 0, 3)\)
Question
The line \(r = i + k + \mu(i – j + 2k)\) and the plane \(2x – y + z + 2 = 0\) intersect at the point \(P\). Find the coordinates of \(P\).
▶️Answer/Explanation
Ans:
\(x = 1 + \mu, y = –\mu, z = 1 + 2\mu\)
\(2(1 + \mu) + \mu + 1 + 2\mu + 2 = 0. \mu = –1 \)
\(P\) is \((0, 1, –1)\) (Accept any form of notation, including vectors.)
Question
The line \(\frac{x-3}{2}=y+1=\frac{5-z}{3}\) and the plane \(2x-y+3z=10\) intersect at the point \(P\). Find the coordinates of \(P\).
▶️Answer/Explanation
Ans:
\(x=2\lambda+3,y=\lambda-1,z=-3\lambda+5\)
\(2(2\lambda+3)-(\lambda-1)+3(-3\lambda+5)=10\)
\(\lambda=2\)
Point of intersection \((7,1,-1)\)
Question
Find the equation of the line of intersection of the two planes \(–4x + y + z = –2\) and \(3x – y + 2z = –1\).
▶️Answer/Explanation
Ans:
EITHER Gaussian elimination is \(r=\begin{pmatrix} 0\\ -1\\ -1\end{pmatrix}+\lambda \begin{pmatrix} 3\\ 11\\ 1\end{pmatrix}\)
OR
Let \(x=0\) ⇒ \(\begin{Bmatrix} y+z=-2\\ -y+2z=-1 \end{Bmatrix}\) ⇒ \(3z = –3, z = –1, y = –1\)⇒ \((0, –1, –1)\)
Let \(z=0\) ⇒ \(\begin{Bmatrix} -4x+y=-2\\ 3x-y=-1 \end{Bmatrix}\) ⇒ \(–x = –3, x = 3, y = 10\)⇒ \((3, 10, 0)\)
The equation of the line of intersection is \(r=\begin{pmatrix} 0\\ -1\\ -1\end{pmatrix}+\lambda \begin{pmatrix} 3\\ 11\\ 1\end{pmatrix}\) (or equivalent)
Question
Find an equation for the line of intersection of the following two planes.
\(x + 2y – 3z = 2\)
\(2x + 3y – 5z = 3\)
▶️Answer/Explanation
Ans:
METHOD 1
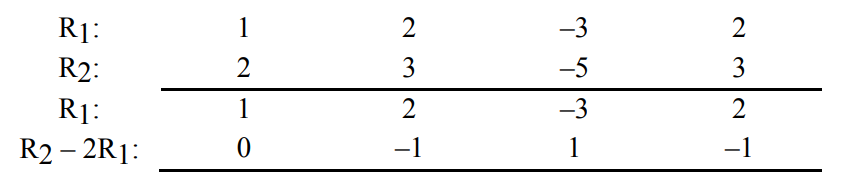
Let \(z = t\), then \(y = t + 1\) and \(x = t\).
Therefore the line of intersection is \(x = t, y = t + 1, z = t\) (or equivalent).
METHOD 2
Let \(z = 0 => x + 2y = 2 =>x = 0, y = 1\)
\(2x + 3y = 3\)
The direction vector of the line of intersection is \(n_1×n_2\) == \(– i – j – k\)
Therefore the line of intersection is \(r=\begin{pmatrix} 0\\ 1\\ 0\end{pmatrix}+\lambda \begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}\) (or equivalent)
Question
The point \(A\) is the foot of the perpendicular from the point \((1, 1, 9)\) to the plane \(2x + y – z = 6\). Find the coordinates of \(A\).
▶️Answer/Explanation
Ans:
\(\begin{pmatrix} x\\ y\\ z\end{pmatrix}=\begin{pmatrix} 1\\ 1\\ 9\end{pmatrix}+\lambda \begin{pmatrix} 2\\ 1\\ -1\end{pmatrix}\)
Coordinates of foot satisfy
\(2(1 + 2\lambda) + (1 + \lambda) – (9 – \lambda) = 6\)= > \(6\lambda = 12\) = > \(\lambda = 2 \)
Foot of perpendicular is (5, 3, 7)
Question
Let \(P\) be the point \((1,0,– 2)\) and \(Π\) be the plane\( x+ y -2 z +3 = 0 \). Let \(P΄\) be the reflection of \(P\) in the plane \(Π\). Find the coordinates of the point \(P΄\).
▶️Answer/Explanation
Ans:
General point on line is \((1+\lambda,\lambda,-2-2\lambda)\)
Intersection of line and plane
\(1+\lambda+\lambda-2(-2-2\lambda)+3=0\)
⇒\(\lambda=-\frac{4}{3}\)
Note: Allow FT on incorrect \(\lambda\)
⇒ at \(P΄\lambda=2(\frac{-4}{3}) \)
⇒ \(P΄\) is \((\frac{-5}{3}, \frac{-8}{3},\frac{10}{3})\)
Question
Three points \(A, B\) and \(C\) have coordinates \((2, 1, –2), (2, –1, –1)\) and \((1, 2, 2)\) respectively. The vectors \(\overrightarrow{OA}\) , \(\overrightarrow{OB}\) and \(\overrightarrow{OC}\), where \(O\) is the origin, form three concurrent edges of a parallelepiped \(OAPBCQSR\) as shown in the following diagram.
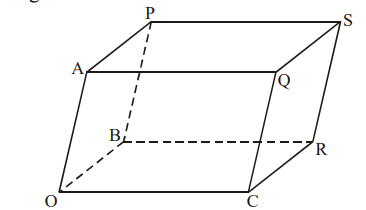
(a) Find the coordinates of \(P, Q, R\) and \(S\).
(b) Find an equation for the plane \(OAPB\).
(c) Calculate the volume, \(V\), of the parallelepiped given that \(V = \overrightarrow{OA} × \overrightarrow{OB} . \overrightarrow{OC}\)
▶️Answer/Explanation
Ans:
(a) \(\overrightarrow{OP}= \overrightarrow{OA} + \overrightarrow{OB} = 4i – 3k\) ⇒ \(P = (4, 0, –3)\)
\(\overrightarrow{OQ} = \overrightarrow{OA}+ \overrightarrow{OC}= 3i + 3j\) ⇒ \(Q = (3, 3, 0)\)
\(\overrightarrow{OR}= \overrightarrow{OB}+ \overrightarrow{OC}= 3i + j + k\) ⇒ \(R = (3, 1, 1) \)
\(\overrightarrow{OS} =\overrightarrow{OP} + \overrightarrow{OC}= 5i + 2j – k\) ⇒ \(S = (5, 2, 1) \)
(b) \(\overrightarrow{OA} × \overrightarrow{OB} = –3i – 2j – 4k\): (from part (i)).
An equation of the plane is \(3x + 2y + 4z = 0\)
(c) \(V = |(–3i – 2j – 4k).(i+ 2j + 2k)| = |–3 – 4 – 8|= 0\)
Note: Accept alternative forms e.g \(r=\lambda \begin{pmatrix} 2\\ 1\\ -2\end{pmatrix}+\mu \begin{pmatrix} 2\\ -1\\ -1\end{pmatrix}\) or \( \begin{pmatrix} -3\\ -2\\ 4\end{pmatrix}.\begin{pmatrix} x\\ y\\ z\end{pmatrix}=0.\)
Question
- The point \(P(1, 2, 11)\) lies in the plane \(\pi_1\) . The vector \(3i – 4 j + k\) is perpendicular to \(\pi_1\) . Find the Cartesian equation of \(\pi_1\).
- The plane \(\pi_2\) has equation \(x + 3y – z = –4\).
- Show that the point \(P\) also lies in the plane \(\pi_2\).
- Find a vector equation of the line of intersection of \(\pi_1\) and \(\pi_2\).
- Find the acute angle between \(\pi_1\) and \(\pi_2\) .
▶️Answer/Explanation
Ans:
- \(\begin{pmatrix} x\\ y\\ z\end{pmatrix}.\begin{pmatrix} 3\\ -4\\ 1\end{pmatrix}=\begin{pmatrix} 1\\ 2\\ 11\end{pmatrix}.\begin{pmatrix} 3\\ -4\\ 1\end{pmatrix}\)⇒ \(3x – 4y + z = 6 \)
- \(1 + 3 × 2 – 11 = –4\)⇒ \(P\) lies in \(\pi_2\).
- \(\begin{pmatrix} 3\\ -4\\ 1\end{pmatrix}×\begin{pmatrix} 1\\ 3\\ -1\end{pmatrix}=\begin{pmatrix} 1\\ 4\\ 13\end{pmatrix} \)
\(r= \begin{pmatrix} 1\\ 2\\ 11\end{pmatrix}+\lambda \begin{pmatrix} 1\\ 4 \\ 13\end{pmatrix}\)
Note: Award (M1)(A0) if equation given in incorrect form.
- METHOD 1
\(\begin{pmatrix} 1\\ 3\\ -1\end{pmatrix}.\begin{pmatrix} 3\\ -4\\ 1\end{pmatrix}=-10\) \(\left | \begin{pmatrix} 1\\ 3\\ -1\end{pmatrix} \right |=\sqrt{11}\) \(\left | \begin{pmatrix} 3\\ -4\\ 1\end{pmatrix} \right |=\sqrt{26}\)
\(cos \theta = \frac{-10}{\sqrt{11}\sqrt{26}}(=–0.5913)\)
\(\theta = 2.2035 radians\) (or \(\theta =\) 126.3°)
The angle between the planes is
\(\pi – 2.2035 = 0.938 radians\) (or 180° – 126.3° = 53.7°)
METHOD 2
\(\left | \begin{pmatrix} 1\\ 3\\ -1\end{pmatrix}× \begin{pmatrix} 3\\ -4\\ 1\end{pmatrix} \right |= \left | \begin{pmatrix} 1\\ 3\\ -1\end{pmatrix} \right | \left | \begin{pmatrix} 3\\ -4\\ 1\end{pmatrix} \right | sin \theta\)
\(\left | \begin{pmatrix} 1\\ 3\\ -1\end{pmatrix}× \begin{pmatrix} 3\\ -4\\ 1\end{pmatrix} \right |= \begin{vmatrix} 1\\ 4\\ 13 \end{vmatrix} = \sqrt{186}\) \(\left | \begin{pmatrix} 1\\ 3\\ -1\end{pmatrix} \right |=\sqrt{11}\) \(\left | \begin{pmatrix} 3\\ -4\\ 1\end{pmatrix} \right |=\sqrt{26}\)
\(sin \theta = \frac{\sqrt{186}}{\sqrt{11}\sqrt{26}}(=0.8064)\)
\(\theta = 0.938 radians\) (or \(\theta =\) 53.7°)
Question
The point \(A (2, 5, –1)\) is on the line \(L\), which is perpendicular to the plane with equation \(x + y + z – 1 = 0\).
- Find the Cartesian equation of the line \(L\)
- Find the point of intersection of the line \(L\) and the plane.
- The point \(A\) is reflected in the plane. Find the coordinates of the image of \(A\).
- Calculate the distance from the point \(B(2, 0, 6)\) to the line \(L\).
▶️Answer/Explanation
Ans:
- \(n= \begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}\), hence the equation of \(L\) through \(A(2, 5, –1)\) is given by \(\frac{x-2}{1}=\frac{y-5}{1}-\frac{z+1}{1}\)
- A general point on \(L\) is \((2 + \lambda, 5 + \lambda, –1 + \lambda)\).
At intersection of line \(L\) and the plane \((2 + \lambda) + (5 +\lambda) + (–1 + \lambda) –1 = 0\)⇒ \(3\lambda = –5\)⇒ \(\lambda= –\frac{5}{3}\)
⇒point of intersection \((\frac{1}{3},\frac{10}{3},\frac{-8}{3})\) - Let \(A′(x, y, z)\) be the reflection of \(A\).
EITHER At \(A′\lambda=-\frac{10}{3}\)⇒ \(A′=(-\frac{4}{3},\frac{5}{3},\frac{-13}{5})\)
OR Since point of intersection of \(L\) and the plane is midpoint of \(AA′\)
⇒ \(A′=(-\frac{4}{3},\frac{5}{3},\frac{-13}{5})\)
Question
The plane \(\pi\) contains the line \(\frac{x-1}{2}=\frac{y-1}{3}=\frac{z-5}{6}\) and the point (1,-2,3).
- Show that the equation of \(\pi\) is \(6x+2y-3z=-7\)
- Calculate the distance of the plane \(\pi\) from the origin.
▶️Answer/Explanation
Ans:
- A vector in the plane is \(\begin{pmatrix} 1\\ 1\\ 5\end{pmatrix}-\begin{pmatrix} 1\\ -2\\ 3\end{pmatrix}=\begin{pmatrix} 0\\ 3\\ 2\end{pmatrix} \)
Normal vector to the plane is \(\begin{pmatrix} 0\\ 3\\ 2\end{pmatrix}×\begin{pmatrix} 2\\ 3\\ 6\end{pmatrix}=\begin{pmatrix} 12\\ 4\\ -6\end{pmatrix} \)
Equation of the plane is \(r.\begin{pmatrix} 6\\ 2\\ -3\end{pmatrix}=\begin{pmatrix} 1\\ -2\\ 3\end{pmatrix}.\begin{pmatrix} 6\\ 2\\ -3\end{pmatrix}\)
\(r.\begin{pmatrix} 6\\ 2\\ -3\end{pmatrix}=6-4-9\)
\(r.\begin{pmatrix} 6\\ 2\\ -3\end{pmatrix}=-7\)
⇒ \(6x+2y-3z=-7\) - Any point \(P\) on normal from origin \(O\) to plane is \((6k,2k,-3k)\)
Distance \(OP=|k\sqrt{6^2+2^2+(-3)^2}|=|7k|\)
\(P\) lies on plane
\(6(6k)+2(2k)-3(-3k)=-7\)
\(36k+4k+9k=-7\)
\(k=-\frac{1}{7}\)
Distance \(=|7×-\frac{1}{7}|=1\)
Question
A plane \(\pi_1\) has equation \(r.\begin{pmatrix} 6\\ 5\\ 4\end{pmatrix}=15\)
- A point \(P (p ,-p ,p )\) lies on plane \(\pi_1\) and \(Q\) is the point where the plane \(\pi_1\) meets the \(y\)-axis.
- Find the coordinates of \(P\) and of \(Q\).
- Show that \(\overrightarrow{PQ}\) is parallel to the vector \(u\), where \(u = i – 2j + k\).
- Another plane \(\pi_2\) intersects \(\pi_1\) in the line \((PQ)\). The point \(T(1,0,–1)\) lies on \(\pi_2\).
- Find the equation of \(\pi_2\), giving your answer in the form \(Ax+By+Cz=D\).
- Find the angle between \(\pi_1\) and \(\pi_2\).
▶️Answer/Explanation
Ans:
- \(\begin{pmatrix} p\\ -p\\ p\end{pmatrix}.\begin{pmatrix} 6\\ 5\\ 4\end{pmatrix}=15\)
\(p=3\)
⇒\(P(3,-3,3)\)(Accept vector form)
\(\begin{pmatrix} 0\\ y\\ 0\end{pmatrix}.\begin{pmatrix} 6\\ 5\\ 4\end{pmatrix}=15\)
⇒\(Q(0,3,0)\)(Accept vector form) - \(\overrightarrow{PQ}= \begin{pmatrix} -3\\ 6\\ 3\end{pmatrix}\)
Since \(\overrightarrow{PQ}\) is a multiple of \(u\)
it is parallel to \(u\)
- \(\overrightarrow{TQ}=\begin{pmatrix} 0\\ 3\\ 0 \end{pmatrix}-\begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix} \)
\(=\begin{pmatrix} -1\\ 3\\ 1 \end{pmatrix} \)
EITHER
\(\begin{vmatrix} i & j & k\\ -1 & 3 & 1\\ 1 & -2 & 1 \end{vmatrix}=5i+2j-k\)
\(r.\begin{pmatrix} 5\\ 2\\ -1 \end{pmatrix}=\begin{pmatrix} 5\\ 2\\ -1 \end{pmatrix}.\begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix} \)
\(5x+2y-z=6\)
OR
\(\begin{pmatrix} x\\ y\\ z \end{pmatrix}=\begin{pmatrix} 3\\ -3\\ 3 \end{pmatrix}+\lambda \begin{pmatrix} 1\\ -2\\ -1 \end{pmatrix}+\mu \begin{pmatrix} -1\\ 3\\ 1 \end{pmatrix}\)
\(x=3+\lambda-\mu\)
\(y=-3-2\lambda+3\mu\)
\(z=3+\lambda+\mu\)
Eliminating \(\lambda,\mu\)
\(5x+2y-z=6\) - \(cos \theta = \frac{\begin{pmatrix} 5\\ 2\\ -1 \end{pmatrix}.\begin{pmatrix} 6\\ 5\\ 4 \end{pmatrix}}{\sqrt{30}\sqrt{77}}\)
\(cos \theta = \frac{36}{\sqrt{30}\sqrt{77}}\)
\(\theta=41.5\)° (or 0.724 radians) (Accept 139°, 2.42 radians)
- \(\begin{pmatrix} p\\ -p\\ p\end{pmatrix}.\begin{pmatrix} 6\\ 5\\ 4\end{pmatrix}=15\)
Question
- Solve the following system of linear equations
\(x + 3y – 2z = –6\)
\(2x + y + 3z = 7\)
\(3x – y + z = 6\) - Find the vector \(v = (i + 3j – 2k) × (2i + j + 3k)\)
- If \(a = i + 3j – 2k, b = 2i + j + 3k\) and \(u = ma + nb\) where \(m, n\) are scalars, and \(u \neq o\) , show that \(v\) is perpendicular to \(u\) for all \(m\) and \(n\).
- The line \(l\) lies in the plane \(3x – y + z = 6\) , passes through the point \((1, –1, 2)\) and is perpendicular to \(v\). Find the equation of \(l\).
▶️Answer/Explanation
Ans:
- The system is \(\begin{pmatrix} 1&3&-2\\ 2&1&3\\ 3&-1&1 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\end{pmatrix}=\begin{pmatrix} -6\\ 7\\ 6 \end{pmatrix}\)
⇒ \(\begin{pmatrix} x\\ y\\ z\end{pmatrix}= \begin{pmatrix} 1&3&-2\\ 2&1&3\\ 3&-1&1\end{pmatrix}^{-1}\begin{pmatrix} -6\\ 7\\ 6\end{pmatrix}=\begin{pmatrix} 1\\ -1\\ 2\end{pmatrix}\)
Therefore, the solution is \(x=1,y=-1,z=2\)
OR
By Guass elimination
Back substitution gives \(x=1,y=-1,z=2\)
OR
\(x=1,y=-1,z=2\) - \(v=\begin{vmatrix} i&j&k\\ 1&3&-2\\ 2&1&3 \end{vmatrix}=\begin{vmatrix} 3&-2\\ 1&3 \end{vmatrix}i-\begin{vmatrix} 1&-2\\ 2&3 \end{vmatrix}j+\begin{vmatrix} 1&3\\ 2&1 \end{vmatrix}k=11i-7j-5k\)
- \(u = m(i + 3j – 2k) + n(2i + j + 3k)
= (m + 2n)i + (3m + n)j + (–2m + 3n)k\)
Therefore, \(v . u = 11(m + 2n) – 7(3m + n) – 5(–2m + 3n)\)
\(= 11m + 22n – 21m – 7n + 10m – 15n\)
\(= 0,\) for all \(m\) and \(n\).
That is, \(v\) is perpendicular to \(u\) for all values of \(m\) and \(n\).
OR
\(v\) is perpendicular to both \(a\) and \(b\) [from part (b)].
Therefore, \(v . a = v . b = 0,\) so \(v . u = m(v . a) + n(v . b) = 0,\)
and hence \(v\) is perpendicular to \(u\) for all values of \(m\) and \(n\). - The normal to the plane, \(3i – j + k\), and \(v\) are both perpendicular to the required line, \(l\).
Therefore, the direction of \(l\) is given by
\(v×(3i–j+k) = \begin{vmatrix} i&j&k\\ 11&-7&-5\\ 3&-1&1 \end{vmatrix}= \begin{vmatrix} -7&-5\\ -1&1 \end{vmatrix}i-\begin{vmatrix} 11&-5\\ 3&1 \end{vmatrix}j+\begin{vmatrix} 11&-7\\ 3&-1 \end{vmatrix}k = –12i – 26j + 10k\)
Thus, an equation for \(l\) is \(r = i – j + 2k + \lambda(6i + 13j – 5k),\)
where \(\lambda\) is a scalar.
[Any form of the correct answer is quite acceptable.]
Question
The coordinates of the points \(P, Q, R\) and \(S\) are \((4,1,–1), (3,3,5), (1,0, 2c),\) and \((1,1,2),\) respectively.
- Find the value of \(c\) so that the vectors \(\overrightarrow{QR}\) and \(\overrightarrow{PR}\) are orthogonal.
For the remainder of the question, use the value of \(c\) found in part (a) for the coordinate of the point \(R\). - Evaluate \(\overrightarrow{PS} × \overrightarrow{PR}\) .
- Find an equation of the line \(l\) which passes through the point \(Q\) and is parallel to the vector \(\overrightarrow{PR}\).
- Find an equation of the plane \(\pi\) which contains the line \(l\) and passes through the point \(S\).
- Find the shortest distance between the point \(P\) and the plane \(\pi\).
▶️Answer/Explanation
Ans:
- Since the coordinates of the points \(P, Q\) and \(R\) are \((4, 1, –1), (3, 3, 5)\) and \((1, 0, 2c),\) respectively, the vectors \(\overrightarrow{QR}\) and \(\overrightarrow{PR}\) are given by
\(\overrightarrow{QR}\) = \(−2\overrightarrow{i} − 3\overrightarrow{j} + (2c − 5)\overrightarrow{k}\)
\(\overrightarrow{PR}\) = \(−3\overrightarrow{i} − \overrightarrow{j} + (2c + 1)\overrightarrow{k}\)
\(\overrightarrow{QR}\) is perpendicular to \(\overrightarrow{PR}\) if and only if \(\overrightarrow{QR} ⋅\overrightarrow{PR} = 0\)
\(i.e. 6 + 3 + (2c – 5)(2c +1) = 0 \)
⇒ \(4c^ 2 – 8c + 4 = 0\)⇒ \((c – 1)^2 = 0\)⇒ \(c = 1\) - \(\overrightarrow{PR}=-3\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k}, \overrightarrow{PS}=-3\overrightarrow{i}+3\overrightarrow{k}\)
\(\overrightarrow{PS}×\overrightarrow{PR}= \begin{vmatrix} \overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}\\ -3&0&3\\ -3&-1&3 \end{vmatrix}=3\overrightarrow{i}+3\overrightarrow{k}\) - The parametric equation of a line \(l\) which passes through the point \((3, 3, 5)\) and is parallel to the vector \(\overrightarrow{PR}\) is given by
\(\overrightarrow{r}=(3\overrightarrow{i}+3\overrightarrow{j}+5\overrightarrow{k})+t(-3\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k})\)
\(=3(1-t)\overrightarrow{i}+(3-t)\overrightarrow{j}+(5+3t)\overrightarrow{k}(-∞<t<∞) \) - Let \(P_1\) and \(P_2\) be points on the line \(l\) corresponding to \(t = 0\) and \(t = 1\), respectively.
Hence, for \(\overrightarrow{r}= x\overrightarrow{i} + y \overrightarrow{j}+ z\overrightarrow{k} , x = 3(1 – t), y = (3 – t)\) and \(z = 5 + 3t\).
Putting \(t = 0\) and \(t = 1,\) we get the coordinates of points \(P_1\) and \(P_2\) as (3, 3, 5) and (0, 2, 8), respectively.
Vectors \(\overrightarrow{SP_1}\) , and \(\overrightarrow{SP_2}\) are given by \(\overrightarrow{SP_1}=2\overrightarrow{i}+2\overrightarrow{j}+3\overrightarrow{k}\) and \(\overrightarrow{SP_2}=-\overrightarrow{i}+\overrightarrow{j}+6\overrightarrow{k}\)
A vector perpendicular to both \(\overrightarrow{SP_1}\) and \(\overrightarrow{SP_2}\) is \(\overrightarrow{SP_1}×\overrightarrow{SP_2}=\begin{vmatrix} \overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}\\ 2&2&3\\ -1&1&6 \end{vmatrix}\)
\(= -9\overrightarrow{i}-15\overrightarrow{j}+4\overrightarrow{k}\)
Let \(T(x, y, z)\) be any point of the plane \(\pi\). Since \(S = (1, 1, 2), \overrightarrow{ST}=(x-1)\overrightarrow{i}+(y-1)\overrightarrow{j}+(z-2)\overrightarrow{k}\) is a vector in \(\pi .\) Hence \(\overrightarrow{TS}.\overrightarrow{n}=0\) \(i.e 9(x – 1) – 15(y – 1) + 4(z – 2) = 0\) ⇒ \(9x – 15y + 4z – 2 = 0\)
OR
\(\overrightarrow{QS}=(1-3)\overrightarrow{i}+(1-3)\overrightarrow{j}+(2-5)\overrightarrow{k}\)
The equation of the plane containing the line \(l\) and passing through the point \(S\) is determined by \(l\) and the vector \(\overrightarrow{SQ}\) .
Hence, the equation is: \(\overrightarrow{r}= \begin{pmatrix} 3\\ 3\\ 5\end{pmatrix}+\lambda \begin{pmatrix} -3\\ -1\\ 3\end{pmatrix}+\mu \begin{pmatrix} -2\\ -2\\ 3\end{pmatrix}\) - Shortest distance \(\frac{|\overrightarrow{PQ}.\overrightarrow{n}|}{|\overrightarrow{n}|}=\frac{\left | \begin{pmatrix} -1\\ 2\\ 6 \end{pmatrix}. \begin{pmatrix} 9\\ -15\\ 4 \end{pmatrix} \right |}{\sqrt{322}}\)
\(=\frac{15}{\sqrt{322}}\) Accept 0.836 (3 s.f.)
Question
The coordinates of the points \(P, Q, R\) and \(S\) are \((4,1,–1), (3,3,5), (1,0, 2c),\) and \((1,1,2),\) respectively.
- Find the value of \(c\) so that the vectors \(\overrightarrow{QR}\) and \(\overrightarrow{PR}\) are orthogonal.
For the remainder of the question, use the value of \(c\) found in part (a) for the coordinate of the point \(R\). - Evaluate \(\overrightarrow{PS} × \overrightarrow{PR}\) .
- Find an equation of the line \(l\) which passes through the point \(Q\) and is parallel to the vector \(\overrightarrow{PR}\).
- Find an equation of the plane \(\pi\) which contains the line \(l\) and passes through the point \(S\).
- Find the shortest distance between the point \(P\) and the plane \(\pi\).
▶️Answer/Explanation
Ans:
- Since the coordinates of the points \(P, Q\) and \(R\) are \((4, 1, –1), (3, 3, 5)\) and \((1, 0, 2c),\) respectively, the vectors \(\overrightarrow{QR}\) and \(\overrightarrow{PR}\) are given by
\(\overrightarrow{QR}\) = \(−2\overrightarrow{i} − 3\overrightarrow{j} + (2c − 5)\overrightarrow{k}\)
\(\overrightarrow{PR}\) = \(−3\overrightarrow{i} − \overrightarrow{j} + (2c + 1)\overrightarrow{k}\)
\(\overrightarrow{QR}\) is perpendicular to \(\overrightarrow{PR}\) if and only if \(\overrightarrow{QR} ⋅\overrightarrow{PR} = 0\)
\(i.e. 6 + 3 + (2c – 5)(2c +1) = 0 \)
⇒ \(4c^ 2 – 8c + 4 = 0\)⇒ \((c – 1)^2 = 0\)⇒ \(c = 1\) - \(\overrightarrow{PR}=-3\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k}, \overrightarrow{PS}=-3\overrightarrow{i}+3\overrightarrow{k}\)
\(\overrightarrow{PS}×\overrightarrow{PR}= \begin{vmatrix} \overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}\\ -3&0&3\\ -3&-1&3 \end{vmatrix}=3\overrightarrow{i}+3\overrightarrow{k}\) - The parametric equation of a line \(l\) which passes through the point \((3, 3, 5)\) and is parallel to the vector \(\overrightarrow{PR}\) is given by
\(\overrightarrow{r}=(3\overrightarrow{i}+3\overrightarrow{j}+5\overrightarrow{k})+t(-3\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k})\)
\(=3(1-t)\overrightarrow{i}+(3-t)\overrightarrow{j}+(5+3t)\overrightarrow{k}(-∞<t<∞) \) - Let \(P_1\) and \(P_2\) be points on the line \(l\) corresponding to \(t = 0\) and \(t = 1\), respectively.
Hence, for \(\overrightarrow{r}= x\overrightarrow{i} + y \overrightarrow{j}+ z\overrightarrow{k} , x = 3(1 – t), y = (3 – t)\) and \(z = 5 + 3t\).
Putting \(t = 0\) and \(t = 1,\) we get the coordinates of points \(P_1\) and \(P_2\) as (3, 3, 5) and (0, 2, 8), respectively.
Vectors \(\overrightarrow{SP_1}\) , and \(\overrightarrow{SP_2}\) are given by \(\overrightarrow{SP_1}=2\overrightarrow{i}+2\overrightarrow{j}+3\overrightarrow{k}\) and \(\overrightarrow{SP_2}=-\overrightarrow{i}+\overrightarrow{j}+6\overrightarrow{k}\)
A vector perpendicular to both \(\overrightarrow{SP_1}\) and \(\overrightarrow{SP_2}\) is \(\overrightarrow{SP_1}×\overrightarrow{SP_2}=\begin{vmatrix} \overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}\\ 2&2&3\\ -1&1&6 \end{vmatrix}\)
\(= -9\overrightarrow{i}-15\overrightarrow{j}+4\overrightarrow{k}\)
Let \(T(x, y, z)\) be any point of the plane \(\pi\). Since \(S = (1, 1, 2), \overrightarrow{ST}=(x-1)\overrightarrow{i}+(y-1)\overrightarrow{j}+(z-2)\overrightarrow{k}\) is a vector in \(\pi .\) Hence \(\overrightarrow{TS}.\overrightarrow{n}=0\) \(i.e 9(x – 1) – 15(y – 1) + 4(z – 2) = 0\) ⇒ \(9x – 15y + 4z – 2 = 0\)
OR
\(\overrightarrow{QS}=(1-3)\overrightarrow{i}+(1-3)\overrightarrow{j}+(2-5)\overrightarrow{k}\)
The equation of the plane containing the line \(l\) and passing through the point \(S\) is determined by \(l\) and the vector \(\overrightarrow{SQ}\) .
Hence, the equation is: \(\overrightarrow{r}= \begin{pmatrix} 3\\ 3\\ 5\end{pmatrix}+\lambda \begin{pmatrix} -3\\ -1\\ 3\end{pmatrix}+\mu \begin{pmatrix} -2\\ -2\\ 3\end{pmatrix}\) - Shortest distance \(\frac{|\overrightarrow{PQ}.\overrightarrow{n}|}{|\overrightarrow{n}|}=\frac{\left | \begin{pmatrix} -1\\ 2\\ 6 \end{pmatrix}. \begin{pmatrix} 9\\ -15\\ 4 \end{pmatrix} \right |}{\sqrt{322}}\)
\(=\frac{15}{\sqrt{322}}\) Accept 0.836 (3 s.f.)
Question
Consider the points \(A(1, 2, 1), B(0, –1, 2), C(1, 0, 2)\) and \(D(2, –1, –6)\).
- Find the vectors \(\overrightarrow{AB}\) and \(\overrightarrow{BC}\).
- Calculate \(\overrightarrow{AB}× \overrightarrow{BC}\).
- Hence, or otherwise find the area of triangle \(ABC\).
- Find the Cartesian equation of the plane \(P\) containing the points \(A, B\) and \(C\).
- Find a set of parametric equations for the line \(L\) through the point \(D\) and perpendicular to the plane \(P\).
- Find the point of intersection \(E\), of the line \(L\) and the plane \(P\).
- Find the distance from the point \(D\) to the plane \(P\).
- Find a unit vector that is perpendicular to the plane \(P\).
- The point \(F\) is a reflection of \(D\) in the plane \(P\). Find the coordinates of \(F\).
▶️Answer/Explanation
Ans:
- \(\overrightarrow{AB}=-i-3j+k, \overrightarrow{BC}=i+j\)
- \(\overrightarrow{AB}×\overrightarrow{BC} = \begin{vmatrix} i&j&k\\ -1&-3&1\\ 1&1&0\end{vmatrix} = -i+j+2k\)
- Area of △\(ABC\) = \(\frac{1}{2}|-i+j+2k|=\frac{1}{2}\sqrt{1+1+4}=\frac{\sqrt{6}}{2}\)
- A normal to the plane is given by \(n=\overrightarrow{AB}×\overrightarrow{BC} =-i+j+2k\)
Therefore, the equation of the plane is of the form \(–x + y + 2z = g\)
and since the plane contains A, then \(–1 + 2 + 2 = g\) ⇒ \(g = 3\).
Hence, an equation of the plane is \(–x + y + 2z = 3\). - Vector \(n\) above is parallel to the required line.
Therefore,
\(x = 2 – t\)
\(y = – 1 + t\)
\(z = – 6 + 2t\) - \(–x + y + 2z = 3\)
\(–2 + t – 1 + t – 12 + 4t = 3\)
\(–15 + 6t = 3\)
\(6t = 18 \)
\(t = 3 \)
Point of intersection \((–1, 2, 0)\) - Distance = \(\sqrt{3^2+3^2+6^2}=\sqrt{54}\)
- Unit vector in the direction of \(n\) is \(e=\frac{1}{|n|}×n=\frac{1}{\sqrt{6}}(-i+j+2k)\)
Note: \(-e\) is also acceptable. - Point of intersection of \(L\) and \(P\) is \((-1,2,0)\).
\(\overrightarrow{DE}= \begin{pmatrix} -3\\ 3\\ 6\end{pmatrix}\) ⇒ \(\overrightarrow{EF}= \begin{pmatrix} -3\\ 3\\ 6\end{pmatrix}\)
⇒ coordinates of \(F\) are \((–4, 5, 6)\)
Question
The points \(A, B, C, D\) have the following coordinates
\(A : (1, 3, 1) B : (1, 2, 4) C : (2, 3, 6) D : (5, – 2, 1).\)
- Evaluate the vector product \(\overrightarrow{AB} × \overrightarrow{AC}\), giving your answer in terms of the unit vectors \(i, j, k\).
- Find the area of the triangle \(ABC\).
The plane containing the points \(A, B, C\) is denoted by \(Π\) and the line passing through \(D\) perpendicular to \(Π\) is denoted by \(L\). The point of intersection of \(L\) and \(Π\) is denoted by \(P\). - Find the cartesian equation of \(Π\).
- Find the cartesian equation of \(L\).
- Determine the coordinates of \(P\).
- Find the perpendicular distance of \(D\) from \(Π\)
▶️Answer/Explanation
Ans:
- \(\overrightarrow{AB}=-j+3k\) and \(\overrightarrow{AC}=i+5k\)
\(\overrightarrow{AB}×\overrightarrow{AC}=\begin{vmatrix} i&j&k\\ 0&-1&3\\ 1&0&5\end{vmatrix}=-5i+3j+k\) - Area = \(\frac{1}{2}×|-5i+3j+k|=\frac{\sqrt{35}}{2}\) (accept 2.96)
- The equation of the plane \(Π\) is
\((x, y, z).(–5, 3, 1) = c\), that is, \(– 5x + 3y + z = c\)
where \(c = –5 + 9 + 1 = 5\), that is, \(– 5x + 3y + z = 5\) - Equations of \(L\) are \(\frac{x-5}{-5}=\frac{y+2}{3}=z-1\)
- \(\overrightarrow{AB}=-j+3k\) and \(\overrightarrow{AC}=i+5k\)
- \(L\) meets \(Π\) where
\(5(5-5\lambda)+3(3\lambda-2)+\lambda+1=5\)⇒ \(\lambda=1\)
Point of intersection is (0,1,2). (Accept \(j+2k\)) - Perpendicular distance is \(\sqrt{5^2+3^2+1^2}=\sqrt{35}\)
Question
A line \(l_1\) has equation \(\frac{x+2}{3}=\frac{y}{1}=\frac{z-9}{-2}\)
- Let \(M\) be a point on \(l_1\) with parameter \(\mu\). Express the coordinates of \(M\) in terms of \(\mu\).
- The line \(l_2\) is parallel to \(l_1\) and passes through \(P(4, 0, –3)\).
- Write down an equation for \(l_2\)
- Express \(\overrightarrow{PM}\) in terms of \(\mu\).
- The vector \(\overrightarrow{PM}\) is perpendicular to \(l_1\).
- Find the value of \(\mu\).
- Find the distance between \(l_1\) and \(l_2\)
- The plane \(\pi_1\) contains \(l_1\) and \(l_2\). Find an equation for \(\pi_1\) , giving your answer in the form \(Ax + By + Cz = D.\)
- The plane \(\pi_2\) has equation \(x – 5y – z = –11\). Verify that \(l_1\) is the line of intersection of the planes \(\pi_1\) and \(\pi_2\).
▶️Answer/Explanation
Ans:
- \(M(3\mu-2,\mu,9-2\mu)\)
- \(\frac{x-4}{3}=\frac{y}{1}=\frac{z+3}{-2}\) or \(r=\begin{pmatrix} 4\\ 0\\ -3\end{pmatrix}+\lambda \begin{pmatrix} 3\\ 1\\ -2\end{pmatrix}\)
- \(\overrightarrow{PM}=\begin{pmatrix} 3\mu-2-4\\ \mu\\ 9-2\mu+3\end{pmatrix}=\begin{pmatrix} 3\mu-6\\ \mu\\ 12-2\mu\end{pmatrix}\)
- \(\begin{pmatrix} 3\mu-6\\ \mu\\ 12-2\mu\end{pmatrix}.\begin{pmatrix} 3\\ 1\\ -2\end{pmatrix}=0\)
\(9\mu – 18 + \mu – 24 + 4\mu = 0\)
\(\mu\)=3 - \(\overrightarrow{PM}=\begin{pmatrix} 3\\ 3\\ 6\end{pmatrix}\)
\(|\overrightarrow{PM}|=\sqrt{3^2+3^2+6^2}=3\sqrt{6}\) (accept \(\sqrt{54}\) or 7.35)
- \(\begin{pmatrix} 3\mu-6\\ \mu\\ 12-2\mu\end{pmatrix}.\begin{pmatrix} 3\\ 1\\ -2\end{pmatrix}=0\)
- \(n=\begin{vmatrix} i&j&k\\ 3&3&6\\ 3&1&-2\end{vmatrix}=–12i + 24j – 6k= –6(2i – 4j + k) \)
\(\begin{pmatrix} 2\\ -4\\ 1\end{pmatrix}.r=\begin{pmatrix} 2\\ -4\\ 1\end{pmatrix}.\begin{pmatrix} 4\\ 0\\ -3\end{pmatrix}\)
\(2x – 4y + z = 5\) - EITHER
\(l_1\) is on \(\pi_1\) from part (d).
Testing \(l_1\) on \(\pi_2\) gives \((3\mu – 2) –5(\mu) – (9 – 2\mu) = –11.\)
Therefore \(l_1\) is also on \(\pi_2\) and is therefore the line of intersection.
OR
\(2x – 4y + z = 5\)
\(x-5y-z=-11\)
_____________________
\(3x – 9y = – 6\)
\(x – 3y = –2\)
If \(y = \lambda, x = –2 + 3\lambda, z = –2\lambda + 9\)
or \(\frac{x+2}{3}=\frac{y}{1}=\frac{z-9}{-2}\)which is \(l_1\).
Question
- Show that lines \(\frac{x-2}{1}=\frac{y-2}{3}=\frac{z-3}{1}\) and \(\frac{x-2}{1}=\frac{y-3}{4}=\frac{z-4}{2}\) intersect and find the coordinates of \(P\), the point of intersection.
- Find the Cartesian equation of the plane \(\pi\) that contains the two lines.
- The point \(Q (3, 4, 3)\) lies on \(\pi\). The line \(L\) passes through the midpoint of \([PQ]\). Point \(S\) is on \(L\) such that \(|\overrightarrow{PS}|=|\overrightarrow{QS}|=3\), and the triangle \(PQS\) is normal to the plane \(\pi\). Given that there are two possible positions for \(S\), find their coordinates.
▶️Answer/Explanation
Ans:
- \(L_1: x = 2 + λ ; y = 2 + 3λ ; z = 3 + λ\)
\(L_2: x = 2 + µ ; y = 3 + 4µ ; z = 4 + 2µ\)
At the point of intersection
\(2 + \lambda = 2 + \mu\) (1)
\(2 + 3\lambda = 3 + 4\mu\) (2)
\(3 + \lambda = 4 + 2\mu\) (3)
From (1), \(\lambda = \mu\).
Substituting in (2), \(2 + 3\lambda = 3 + 4\lambda\)
⇒ \(\lambda = \mu = –1.\)
We need to show that these values satisfy (3).
They do because LHS = RHS = 2; therefore the lines intersect.
So \(P\) is \((1, –1, 2).\) - The normal to \(\pi\) is normal to both lines. It is therefore given by the vector product of the two direction vectors.
Therefore, normal vector is given by \(\begin{pmatrix} i&j&k\\ 1&3&1\\ 1&4&2\end{pmatrix}=2i-j+k\)
The Cartesian equation of \(\pi\) is \(2x-y+z=2+1+2\)
\(i.e. 2x-y+z=5\) - The midpoint \(M\) of \([PQ]\) is \((2,\frac{3}{2},\frac{5}{2})\).
The direction of \(\overrightarrow{MS}\) is the same as the normal to \(\pi\),\(i.e. 2i-j+k=5\)
The coordinates of a general point \(R\) on \(\overrightarrow{MS}\) are therefore
\((2+2\lambda,\frac{3}{2}-\lambda,\frac{5}{2}+\lambda)\)
It follows that \(\overrightarrow{PR}=(1+2\lambda)i+(\frac{5}{2}-\lambda)j+(\frac{1}{2}+\lambda)k\)
At \(S\), length of \(\overrightarrow{PR}\) is 3, i.e
\((1+2\lambda)^2+(\frac{5}{2}-\lambda)^2+(\frac{1}{2}+\lambda)^2=9\)
\(1+4\lambda+4\lambda^2+\frac{25}{4}-5\lambda+\lambda^2+\frac{1}{4}+\lambda+\lambda^2=9\)
\(6\lambda^2=\frac{6}{4}\)⇒\(\lambda=\pm \frac{1}{2}\)
Substituting these values,
the possible positions of \(S\) are \((3, 1, 3)\) and \((1, 2, 2)\)
Question
- The plane \(\pi_1\) has equation \(r=\begin{pmatrix} 2\\ 1\\ 1\end{pmatrix}+\lambda \begin{pmatrix} -2\\ 1\\ 8\end{pmatrix}+\mu \begin{pmatrix} 1\\ -3\\ -9\end{pmatrix}\).
The plane \(\pi_2\) has equation \(r=\begin{pmatrix} 2\\ 0\\ 1\end{pmatrix}+s \begin{pmatrix} 1\\ 2\\ 1\end{pmatrix}+t \begin{pmatrix} 1\\ 1\\ 1\end{pmatrix}\).- For points which lie in \(\pi_1\) and \(\pi_2\), show that, \(\lambda=\mu\).
- Hence, or otherwise, find a vector equation of the line of intersection of \(\pi_1\) and \(\pi_2\).
- The plane \(\pi_3\) contains the line \(\frac{2-x}{3}=\frac{y}{-4}=z+1\) and is perpendicular to \(3i-2j+k\). Find the Cartesian equation of \(\pi_3\).
- Find the intersection of \(\pi_1\),\(\pi_2\) and \(\pi_3\).
▶️Answer/Explanation
Ans:
- (1) \(2-2\lambda+\mu=2+s+t\)
(2) \(1+\lambda-3\mu=2s+t\)
(3) \(1+8\lambda-9\mu=1+s+t\)
subtracting (3) from (1)
\(1-10\lambda+10\mu=1\)⇒\(\lambda=\mu\) - On the line of intersection \(\lambda=\mu\)⇒ an equation of the line is
\(r=\begin{pmatrix} 2\\ 1\\ 1\end{pmatrix}+\lambda \begin{pmatrix} -2\\ 1\\ 8\end{pmatrix}+\lambda \begin{pmatrix} 1\\ -3\\ -9\end{pmatrix}=\begin{pmatrix} 2\\ 1\\ 1\end{pmatrix}+\lambda \begin{pmatrix} -1\\ -2\\ -1\end{pmatrix}\)
- (1) \(2-2\lambda+\mu=2+s+t\)
- The plane \(\pi_3\) contains, e.g. the point \((2,0,-1)\).
The equation of the plane is \(\begin{pmatrix} x\\ y\\ z\end{pmatrix}.\begin{pmatrix} 3\\ -2\\ 1\end{pmatrix}=\begin{pmatrix} 2\\ 0\\ -1\end{pmatrix}.\begin{pmatrix} 3\\ -2\\ 1\end{pmatrix}=5\)
The cartesian equation of the plane is \(3x-2y+z=5\). - Intersection line between \(r=\begin{pmatrix} 2\\ 1\\ 1\end{pmatrix}+\lambda \begin{pmatrix} -1\\ -2\\ -1\end{pmatrix}\) and \(\pi_3\).
\(3x-2y+z=5\)⇒\(3(2-\lambda)-2(1-2\lambda)+1-\lambda=5\)
This equation is satisfied by any real value of \(\lambda\)⇒ the 3 planes intersect at the line \(r=\begin{pmatrix} 2\\ 1\\ 1\end{pmatrix}+\lambda \begin{pmatrix} -1\\ -2\\ -1\end{pmatrix}\)
Question
- The line \(l_1\) passes through the point \(A(0,1,2)\) and is perpendicular to the plane \(x-4y-3z=0\). Find the Cartesian equations of \(l_1\).
- The line \(l_2\) is parallel to \(l_1\)and passes through the point \(P(3,-8,-11)\). Find the vector equation of the line \(l_2\).
- The point \(Q\) on the line \(l_1\) such that \(\overrightarrow{PQ}\) is perpendicular to \(l_1\) and \(l_1\). Find the coordinates of \(Q\).
- Hence find the distance between \(l_1\) and \(l_2\).
▶️Answer/Explanation
Ans:
- Direction vector of \(l_1=\begin{pmatrix} 1\\ -4\\ -3\end{pmatrix}\)
⇒ Equations of line through point \(A\) are: \(\frac{x}{1}=\frac{y-1}{-4}=\frac{z-2}{-3}\)
Note: Accept any correct cartesian form. - Direction vector of \(l_2=\begin{pmatrix} 1\\ -4\\ -3\end{pmatrix}\)
⇒ vector equation of \(l_2\) is \(r=\begin{pmatrix} 3\\ -8\\ -11\end{pmatrix}+\mu \begin{pmatrix} 1\\ -4\\ -3\end{pmatrix}\)
Note: Accept only this form but allow \(\begin{pmatrix} x\\ y\\ z\end{pmatrix}\) in place of \(r\)- General point on \(\_1\) is \((\lambda,1-4\lambda,2-3\lambda)\)
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}\)
\(=\begin{pmatrix} \lambda\\ 1-4\lambda\\ 2-3\lambda\end{pmatrix}-\begin{pmatrix} 3\\ -8\\ -11\end{pmatrix} =\begin{pmatrix} \lambda-3\\ 9-4\lambda\\ 13-3\lambda\end{pmatrix}\)
⇒\(\overrightarrow{PQ}.\overrightarrow{l_1}=0\)
\(=\begin{pmatrix} \lambda-3\\ 9-4\lambda\\ 13-3\lambda\end{pmatrix}.\begin{pmatrix} 1\\ -4\\ -3\end{pmatrix}=0\)
⇒\(\lambda-3-36+16\lambda-39+9\lambda=0\)
⇒\(26\lambda=78\)⇒\(\lambda=3\)
⇒\(Q=(3,-11,-7)\) - \(d=|\overrightarrow{PQ}|\)\(=\sqrt{0+9+16}=5\)
- General point on \(\_1\) is \((\lambda,1-4\lambda,2-3\lambda)\)
Question
Let \(A\) be the point \((2,-1,0)\),\(B\) the point \((3,0,1)\) and \(C\) the point \((1,m,2)\), where \(m\)∈\(Z,m<0\).
- Find the scalar product \(\overrightarrow{BA}.\overrightarrow{BC}\).
- Hence, given that \(\widehat{ABC}=arccos \frac{\sqrt{2}}{3},\) show that \(m=-1\).
- Determine the Cartesian equation of the plane \(ABC\)
- Find the area of triangle \(ABC\)
- The line \(L\) is perpendicular to plane \(ABC\) and passes through \(A\). Find a vector equation of \(L\).
- The point \(D(6,-7,2)\) lies on \(L\). Find the volume of the pyramid \(ABCD\).
▶️Answer/Explanation
Ans:
- \(\overrightarrow{BA}= \begin{pmatrix} -1\\ -1\\ -1\end{pmatrix}\) \(\overrightarrow{BC}=\begin{pmatrix} -2\\ m\\ 1\end{pmatrix}\)
\(\overrightarrow{BA}.\overrightarrow{BC}=1-m\) - \(\overrightarrow{BA}.\overrightarrow{BC}=|\overrightarrow{BA}||\overrightarrow{BC}|cos \widehat{ABC}\)
\(1-m=\sqrt{3}\sqrt{5+m^2}×\frac{\sqrt{2}}{3}\)
EITHER
\((1-m)^2=\frac{2}{3}(5+m^2)\)⇒\((m^2-6m-7=0)\)
Solving(gives \(m=-1\) or \(m=7)\)
⇒\(m=-1\)
OR
For a correct \(GDC\) sketch
Showing \(m=-1\) is the point of intersection
⇒\(m=-1\)
- \(\overrightarrow{BA}= \begin{pmatrix} -1\\ -1\\ -1\end{pmatrix}\) \(\overrightarrow{BC}=\begin{pmatrix} -2\\ m\\ 1\end{pmatrix}\)
- Using vector product
\(n=\begin{vmatrix} i&j&k\\ -1&-1&-1\\ -2&-1&1\end{vmatrix}=-2i+3j-k\)
Substituting coordinates of a point (e.g. \(A(2,-1,0)\))
⇒\(-2(x-2)+3(y+1)-z=0 (-2x+3y-z=-7)\) - Area \(ABC=\frac{1}{2}|\overrightarrow{BA}×\overrightarrow{BC}|\)
\(=\frac{1}{2}\left | \begin{pmatrix} -2\\ 3\\ -1\end{pmatrix} \right |\)
\(=\frac{\sqrt{14}}{2}(=1.87)\)- line perpendicular to plane \(ABC\) ⇒ line parallel to \(n\)
equation of line is \(r=\begin{pmatrix} 2\\ -1\\ 0\end{pmatrix}+\lambda \begin{pmatrix} -2\\ 3\\ -1\end{pmatrix}\) - \(\overrightarrow{AD}=\begin{pmatrix} 4\\ -6\\ 2\end{pmatrix}\)
volume of pyramid
\(=\frac{1}{3}\) area \(ABC|\overrightarrow{AD}|\)
\(=\frac{1}{3}\frac{\sqrt{14}}{2}\sqrt{56}\)(\(FT\) from any numerical error in \(\overrightarrow{AD}\))
\(=\frac{14}{3}\)(=4.67, accept 4.66)
- line perpendicular to plane \(ABC\) ⇒ line parallel to \(n\)
Question
Two planes \(\pi_1\) and \(\pi_2\) are represented by the equations
\(\pi_1:r=\begin{pmatrix} 3\\ 1\\ 5\end{pmatrix}+\lambda \begin{pmatrix} -2\\ 2\\ 3\end{pmatrix}+\mu \begin{pmatrix} 2\\ 1\\ 0\end{pmatrix}\)
\(\pi_2:2x-y-2z=4\)
- Find \(\begin{pmatrix} -2\\ 2\\ 3\end{pmatrix}×\begin{pmatrix} 2\\ 1\\ 0\end{pmatrix}.\)
- Show that the equation of \(\pi_1\) can be written as \(x-2y+2z=11\)
- Show that \(\pi_1\) is perpendicular to \(\pi_2\)
- The line \(l_1\) is the line of intersection of \(\pi_1\) and \(\pi_2\). Find the vector equation of \(l_1\), giving the answer in parametric form.
- The line \(l_2\) is parallel to both \(\pi_1\) and \(\pi_2\), and passes through \(P(3,-5,-1)\). Find an equation for \(l_2\) in Cartesian form.
- Let \(Q\) be the foot of the perpendicular from \(P\) to the plane \(\pi_2\)
- Find the coordinates of \(Q\)
- Find \(PQ\)
▶️Answer/Explanation
Ans:
Two planes \(\pi_1\) and \(\pi_2\) are represented by the equations
\(\pi_1:r=\begin{pmatrix} 3\\ 1\\ 5\end{pmatrix}+\lambda \begin{pmatrix} -2\\ 2\\ 3\end{pmatrix}+\mu \begin{pmatrix} 2\\ 1\\ 0\end{pmatrix}\)
\(\pi_2:2x-y-2z=4\)- Find \(\begin{pmatrix} -2\\ 2\\ 3\end{pmatrix}×\begin{pmatrix} 2\\ 1\\ 0\end{pmatrix}.\)
- Show that the equation of \(\pi_1\) can be written as \(x-2y+2z=11\)
- Show that \(\pi_1\) is perpendicular to \(\pi_2\)
- The line \(l_1\) is the line of intersection of \(\pi_1\) and \(\pi_2\). Find the vector equation of \(l_1\), giving the answer in parametric form.
- The line \(l_2\) is parallel to both \(\pi_1\) and \(\pi_2\), and passes through \(P(3,-5,-1)\). Find an equation for \(l_2\) in Cartesian form.
- Let \(Q\) be the foot of the perpendicular from \(P\) to the plane \(\pi_2\)
- Find the coordinates of \(Q\)
- Find \(PQ\)
Ans:
- \(\begin{vmatrix} i&j&k\\ -2&2&3\\ 2&1&0\end{vmatrix}=-3i+6j-6k\)
- \(n=i-2j+2k\) so equation of \(\pi_1\) is \(x-2y+2z=D\) (or \(r.n=a.n\))
substituting \((3,1,5)\) ⇒ \(3-2+10=D\)
so \(11=D\)
Therefore the equation of plane \(\pi_1\) is \(x-2y+2z=11\)
- Using scalar product of normal vectors
\(\begin{pmatrix} 1\\ -2\\ 2\end{pmatrix}.\begin{pmatrix} 2\\ -1\\ -2\end{pmatrix}=2+2-4=0\)
The normals are perpendicular, so the planes are perpendicular. - METHOD 1
Elimination of one variable.
Choosing a parameter.
METHOD 2
Finding direction of the line.
Finding a point on the line.
\(x=2\lambda-1;y=2\lambda-6;z=\lambda\)
OR \(\left ( x=\mu+5,y=\mu,z=\frac{1}{2}\mu+3 \right )\)
OR \(\left ( x=t,y=t-5,z=\frac{1}{2}t+\frac{1}{2} \right )\)
OR \(\left ( r= \begin{pmatrix} -1\\ -6\\ 0\end{pmatrix} +\lambda \begin{pmatrix} 2\\ 2\\ 1\end{pmatrix} \right )\) - Direction vector of \(l_2=2i+2j+k\) equation of \(l_2:\frac{x-3}{2}=\frac{y+5}{2}=\frac{z+1}{1}\)
- Recognising that the equation of line \((PQ)\) is needed equation of line \((PQ)\) is \(r=\begin{pmatrix} 3\\ -5\\ -1\end{pmatrix}+t \begin{pmatrix} 2\\ -1\\ -2\end{pmatrix}\)
\(Q\) on \(\pi_2\)⇒ \(2(3+2t)-(-5-t)-2(-1-2t)=4\)
\(t=-1\)⇒\(Q=(1,-4,1)\) - \(PQ=\sqrt{(3-1)^2+(-5+4)^2+(-1-1)^2}=3\)
- Recognising that the equation of line \((PQ)\) is needed equation of line \((PQ)\) is \(r=\begin{pmatrix} 3\\ -5\\ -1\end{pmatrix}+t \begin{pmatrix} 2\\ -1\\ -2\end{pmatrix}\)
- Recognising that the equation of the line \((PQ)\) is needed
equation of line \((PQ)\) is \(r=\begin{pmatrix} 3 \\ -5 \\ -1 \end{pmatrix}+t\begin{pmatrix} 2 \\ -1 \\ -2 \end{pmatrix}\)
\(Q\) on \(\pi_2\)⇒\(2(3+2t)-(-5-t)-2(-1-2t)=4\)
\(t=-1\)
⇒\(Q=1,-4,1)\) - \(PQ=\sqrt{(3-1)^2+(-5+4)^2+(-1-1)^2}=3\)
- Recognising that the equation of the line \((PQ)\) is needed
Question
Consider the vectors \(a=i-j+k,b=i+2j+4k\) and \(c=2i-5j-k\).
- Given that \(c=ma+nb\) where \(m,n\)∈\(Z\), find the value of \(m\) and of \(n\).
- Find a unit vector, \(u\), normal to both \(a\) and \(b\).
- The plane \(\pi_1\) contains the point \(A(1,-1,1)\) and is normal to \(b\). The plane intersects the \(x,y\) and \(z\) axes at the points \(L,M\) and \(N\) respectively.
- Find a Cartesian equation of \(\pi_1\)
- Write down the coordinates of \(L,M\) and \(N\).
- The line through the origin, \(O\), normal to \(\pi_1\) meets \(\pi_1\) at the point \(P\).
- Find the coordinates of \(P\).
- Hence find the distance of \(\pi_1\) from the origin.
- The plane \(\pi_2\) has equation \(x+2y+4z=4\). Calculate the angle between \(\pi_2\) and a line parallel to \(a\).
▶️Answer/Explanation
Ans:
- Substituting for \(a,b\) and \(c\) into \(c=ma+nb\)
Forming any 2 of the following equations
\(m+n=2\) Eq(1)
\(-m+2n=-5\) Eq(2)
\(m+4n=-1\) Eq(3)
Note: Accept equations in vector form.
Solving for \(m\) and \(n\)
\(m=3\) and \(n=-1\) - METHOD 1
\(a×b=\begin{vmatrix} i&j&k\\ 1&-1&1\\ 1&2&4\end{vmatrix}\)
\(=-6i-3j+3k\)
Attempting to find \(|a×b| (=\sqrt{54}=3\sqrt{6})\)
\(u=\frac{1}{\sqrt{54}}(-6i-3j+3k)\left ( =\frac{1}{\sqrt{6}}(-2i-j+k) \right)\)
Note: Award as above for \(b×a=6i+3j-3k\) and \(u=\frac{1}{\sqrt{54}}(6i+3j-3k)\).
METHOD 2
Stating 2 equations derived from \(a.u\) and \(b.u\) where \(u=xi+yj+zk\).
\(x-y+z=0\) Eq(1)
\(x+2y+4z=0\) Eq(2)
Attempting to solve the above system of equations
Solution sets include
\(x=-2z\) and \(y=-z\)
OR \(y=\frac{x}{2}\) and \(z=\frac{-x}{2}\)
OR \(z=-y and x=2y\)
Note: Accept any correct numerical solution such as \(x=2,y=1,z=-1\)
Using \(x^2+y^2+z^2=1 (i.e.|u|=1)\) to find values for \(x,y\) and \(z\).
Either \(u=\frac{1}{\sqrt{6}}(2i+j-k)\) or \(u=\frac{1}{\sqrt{6}}(-2i-j+k)\)
Note: Ignore any additional answers, even if incorrect.- METHOD 1
Equation of \(\pi_1\) is of the form \(x+2y+4z=d\)
Substituting \((1,-1,1)(\)⇒\(d=3)\)
⇒\(x+2y+4z=3\)
METHOD 2
\(r.(i+2j+4k)=d\)
Evaluate the scalar product \(a.(i+2j+4k)(=3)\)
⇒\(x+2y+4z=3\) - \(L(3,0,0),M(0,\frac{3}{2},0)\) and \(N(0,0,\frac{3}{4})\)
- \(P\) has coordinates \((x,y,z)=(\lambda,2\lambda,4\lambda)\)
Substituting the coordinates of \(P\) into the equation of \(\pi_1\)
\(\lambda+4\lambda+16\lambda=3\)
\(\lambda=\frac{1}{7}\)
\(P(\frac{1}{7},\frac{2}{7},\frac{4}{7})\) - Distance=\(\frac{1}{7}\sqrt{1^2+2^2+4^2}\)
\(=\frac{\sqrt{21}}{7}\) or equivalent(=0.655)
- METHOD 1
- (Given \(\theta\) is the angle between \(\pi_2\) and a line and \(\alpha\) is the angle between the normal and a line)
\(cos \alpha = cos(\frac{\pi}{2}-\theta)=sin \theta\)
Using the scalar product e.g. \(sin \theta = \frac{a.b}{|a|.|b|}\) or \(cos \alpha = \frac{a.b}{|a|.|b|}\)
\((sin \theta)=\frac{(i-j+k).(i+2j+4k)}{|i-j+k|.|i+2j+4k|}\)
\(=\frac{1}{\sqrt{7}}\)(or equivalent)
\(\theta=0.388\) (=22.2°) (\(=arcsin \frac{1}{\sqrt{7}}\)) \(P\) has coordinates \((x,y,z)=(\lambda,2\lambda,4\lambda)\)
Substituting the coordinates of \(P\) into the equation of \(\pi_1\)
\(\lambda+4\lambda+16\lambda=3\)
\(\lambda=\frac{1}{7}\)
\(P(\frac{1}{7},\frac{2}{7},\frac{4}{7})\)Distance=\(\frac{1}{7}\sqrt{1^2+2^2+4^2}\)
\(\frac{\sqrt{21}}{7}\) or equivalent (=0.655)
(Given \(\theta\) is the angle between \(\pi_2\) and a line and \(\alpha\) is the angle between the normal and a line)
\(\cos \alpha =\cos (\frac{\pi}{2}-\theta)=\sin \theta\)
Using the scalar product e.g. \(\sin \theta =\frac{a.b}{|a|.|b|}\) or \(\cos \alpha = \frac{a.b}{|a|.|b|}\)
\((\sin \theta)=\frac{(i-j+k).(i+2j+4k)}{|i-j+k|.|i+2j+4k|}\)
=\(\frac{1}{\sqrt{7}}\)(or equivalent)
\(\theta=0.388(=22.2\)°\(=\arcsin \frac{1}{\sqrt{7}})\)
Question
- Write the vector equations of the following lines in parametric form.
\(r_1=\begin{pmatrix} 3\\ 2\\ 7\end{pmatrix}+m\begin{pmatrix} 2\\ -1\\ 2\end{pmatrix}\) \(r_2=\begin{pmatrix} 1\\ 4\\ 2\end{pmatrix}+n\begin{pmatrix} 4\\ -1\\ 1\end{pmatrix}\) - Hence show that these two lines intersect and find the point of intersection, \(A\).
- Find the Cartesian equation of the plane \(Π\) that contains these two lines.
- Let \(B\) be the point of intersection of the plane \(Π\) and the line \(r=\begin{pmatrix} -8\\ -3\\ 0\end{pmatrix}+\lambda \begin{pmatrix} 3\\ 8\\ 2\end{pmatrix}.\) Find the coordinates of \(B\).
- If \(C\) is the mid-point of \(AB\), find the vector equation of the line perpendicular to the plane \(Π\) and passing through \(C\).
▶️Answer/Explanation
Ans:
- \(x = 3 + 2m\)
\(y = 2 – m\)
\(z = 7 + 2m\)
\(x = 1 + 4n\)
\(y = 4 – n\)
\(z = 2 + n\) - \(3 + 2m = 1 + 4n\) ⇒ \(2m – 4n = – 2\)(i)
\(2 – m = 4 – n\) ⇒ \(m – n = –2\)(ii)
\(7 + 2m = 2 + n\) ⇒ \(2m – n = –5\)(iii)
(iii) – (ii) ⇒ \(m = –3\)
⇒ \(n = –1\)
Substitute in (i), \(– 6 + 4 = – 2\). Hence lines intersect.
Point of intersection \(A\) is \((–3, 5, 1)\) - \(\begin{vmatrix} i&j&k\\ 2&-1&2\\ 4&-1&1\end{vmatrix}=\begin{pmatrix} 1\\ 6\\ 2\end{pmatrix}\)
\(r.\begin{pmatrix} 1\\ 6\\ 2\end{pmatrix}=\begin{pmatrix} 3\\ 2\\ 7\end{pmatrix}.\begin{pmatrix} 1\\ 6\\ 2\end{pmatrix}\)
\(r.\begin{pmatrix} 1\\ 6\\ 2\end{pmatrix}=29\)
\(x+6y+2z=29\) - \(x = –8 + 3\lambda\)
\(y = – 3 + 8\lambda\)
\(z = 2\lambda\)
Substitute in equation of plane.
\(–8 + 3\lambda – 18 + 48\lambda + 4\lambda = 29\)
\(55\lambda = 55\)
\(\lambda = 1\)
Coordinates of \(B\) are \((–5, 5, 2)\) - Coordinates of \(C\) are \((–4, 5, \frac{3}{2})\)
\(r=\begin{pmatrix} -4\\ 5\\ \frac{3}{2}\end{pmatrix}+\mu \begin{pmatrix} 1\\ 6\\ 2\end{pmatrix}\)
Question
The points \(A, B, C\) have position vectors \(i + j + 2k, i + 2 j + 3k, 3i + k\) respectively and lie in the plane \(\pi\).
- Find
- the area of the triangle \(ABC\);
- the shortest distance from \(C\) to the line \(AB\);
- the cartesian equation of the plane \(\pi\).
The line \(L\) passes through the origin and is normal to the plane \(\pi\), it intersects \(\pi\) at the point \(D\).
- Find
- the coordinates of the point \(D\);
- the distance of \(\pi\) from the origin
▶️Answer/Explanation
Ans:
a.
- \(\overrightarrow{AB}=b-a=\begin{pmatrix} 1\\ 2\\ 3\end{pmatrix}-\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}=\begin{pmatrix} 0\\ 1\\ 1\end{pmatrix}\) \(\overrightarrow{AC}=c-a=\begin{pmatrix} 3\\ 0\\ 1\end{pmatrix}-\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}=\begin{pmatrix} 2\\ -1\\ -1\end{pmatrix}\)
\(\overrightarrow{AB}×\overrightarrow{AC}=\begin{vmatrix} i&j&k\\ 0&1&1\\ 2&-1&-1\end{vmatrix}=i(-1+1)-j(0-2)+k(0-2)=2j-2k\)
Area of triangle \(ABC=\frac{1}{2}|2j-2k|=\frac{1}{2}\sqrt{8}(=\sqrt{2})sq.units\) - \(AB=\sqrt{2}\)
\(\sqrt{2}=\frac{1}{2}AB×h=\frac{1}{2}\sqrt{2}×h, h\) is the shortest distance ⇒ \(h=2\) - METHOD 1
\(\pi\) has form \(r.\begin{pmatrix} 0\\ 2\\ -2\end{pmatrix}=d\)
Since \((1,1,2)\) is on the plane \(d=\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}.\begin{pmatrix} 1\\ 2\\ -2\end{pmatrix}=2-4=-2\)
Hence \(2y-2z=-2\)(or \(y-z=-1\))
METHOD 2
\(r=\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}+\lambda \begin{pmatrix} 0\\ 1\\ 1\end{pmatrix}+\mu \begin{pmatrix} 2\\ -1\\ -1\end{pmatrix}\)
\(x = 1 + 2\mu\) (i)
\(y = 1 + \lambda − \mu\) (ii)
\(z = 2 + \lambda − \mu\) (iii)
From (i) \(\mu=\frac{x-1}{2}\)
substitute in (ii) \(y=1+\lambda-(\frac{x-1}{2})\)⇒\(\lambda=y-1+(\frac{x-1}{2})\)
substitute \(\lambda\) and \(\mu\) in (iii)
⇒ \(z=2+y-1+(\frac{x-1}{2})-(\frac{x-1}{2})\)⇒\(y-z=-1\)
b.
- The equation of \(OD\) is
\(r=\lambda \begin{pmatrix} 0\\ 2\\ -2\end{pmatrix},\left ( (or) r=\lambda \begin{pmatrix} 0\\ 1\\ -1\end{pmatrix} \right)\)
This meets \(\pi\) where
\(2\lambda+2\lambda=-1\)⇒\(\lambda=-\frac{1}{4}\)
Coordinates of \(D\) are \((0,-\frac{1}{2},\frac{1}{2})\) - \(|\overrightarrow{OD}|=\sqrt{0+(-\frac{1}{2})^2+(\frac{1}{2})^2}=\frac{1}{\sqrt{2}}\)
- \(\overrightarrow{AB}=b-a=\begin{pmatrix} 1\\ 2\\ 3\end{pmatrix}-\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}=\begin{pmatrix} 0\\ 1\\ 1\end{pmatrix}\) \(\overrightarrow{AC}=c-a=\begin{pmatrix} 3\\ 0\\ 1\end{pmatrix}-\begin{pmatrix} 1\\ 1\\ 2\end{pmatrix}=\begin{pmatrix} 2\\ -1\\ -1\end{pmatrix}\)
