Question
Mary, three female friends, and her brother, Peter, attend the theatre. In the theatre there is a row of 10 empty seats. For the first half of the show, they decide to sit next to each other in
this row.
(a) Find the number of ways these five people can be seated in this row.
For the second half of the show, they return to the same row of 10 empty seats. The four girls decide to sit at least one seat apart from Peter. The four girls do not have to sit next to each other.
(b) Find the number of ways these five people can now be seated in this row.
▶️Answer/Explanation
Ans:
(a) 6 × 5!
= 720 ( accept 6!)
(b) METHOD 1
(Peter apart from girls, in an end seat) 8P4 (=1680) OR
(Peter apart from girls, not in end seat) 7P4 (=840)
case 1: Peter at either end
2 × 8P4 (=3360) OR 2 × 8C4 × 4!(=3360)
case 2: Peter not at the end
8 × 7P4 (=6720) OR 8 × 7C4 × 4!(=6720)
Total number of ways = 3360 + 6720
=10080
METHOD 2
(Peter next to girl, in an end seat) 4 × 8P3 (=1344) OR
(Peter next to one girl, not in end seat) 2 × 4 × 7P3 (=1680) OR
(Peter next to two girls, not in end seat) 4 × 3 × 7P2 (=504)
case 1: Peter at either end
2 × 4 × 8P3 (=2688)
case 2: Peter not at the end
8(2 × 4 × 7P3 + 4 × 3 × 7P2 ) (=17472)
Total number of ways = 10P5 – (2688 + 17472)
= 10080
Question
A continuous random variable \(X\) has a probability density function given by the function \(f(x)\) , where
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k{{\left( {x + 2} \right)}^2},}&{ – 2 \leqslant x < 0} \\
{k,}&{0 \leqslant x \leqslant \frac{4}{3}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the value of \(k\) .
Hence find
(i) the mean of \(X\) ;
(ii) the median of \(X\) .
▶️Answer/Explanation
Markscheme
\(k\int_{ – 2}^0 {{{\left( {x + 2} \right)}^2}} {\text{d}}x + \int_0^{\frac{4}{3}} {k{\text{d}}x} = 1\) M1
\(\frac{{8k}}{3} + \frac{{4k}}{3} = 1\)
\(k = \frac{1}{4}\) A1
Note: Only ft on positive values of \(k\).
[2 marks]
(i) \({\text{E}}(X) = \frac{1}{4}{\int_{ – 2}^0 {x\left( {x + 2} \right)} ^2}{\text{d}}x + \frac{1}{4}\int_0^{\frac{4}{3}} {x{\text{d}}x} \) M1
\( = \frac{1}{4} \times \frac{{ – 4}}{3} + \frac{2}{9}\)
\( = – \frac{1}{9}\) (\( – 0.111\)) A1
(ii) median given by a such that \({\text{P}}(X < a) = 0.5\)
\(\frac{1}{4}{\int_{ – 2}^a {\left( {x + 2} \right)} ^2}{\text{d}}x = 0.5\) M1
\(\left[ {\frac{{{{\left( {x + 2} \right)}^3}}}{3}} \right]_{ – 2}^a = 2\) (A1)
\({\left( {a + 2} \right)^3} – 0 = 6\)
\(a = \sqrt[3]{6} – 2\) (\(= – 0.183\)) A1
[5 marks]
Examiners report
Many candidates recognised that integration was the appropriate technique to solve this question but the fact that the function was piecewise proved problematic for many. Good use of technology by some candidates was seen but few sketches of the function were made. A sketch would have been helpful to many candidates when attempting to solve (b (ii).
Many candidates recognised that integration was the appropriate technique to solve this question but the fact that the function was piecewise proved problematic for many. Good use of technology by some candidates was seen but few sketches of the function were made. A sketch would have been helpful to many candidates when attempting to solve (b (ii).
Question
A set of 15 observations has mean 11.5 and variance 9.3. One observation of 22.1 is considered unreliable and is removed. Find the mean and variance of the remaining 14 observations.
▶️Answer/Explanation
Markscheme
\(\frac{{\sum\limits_{i = 1}^{15} {{x_i}} }}{{15}} = 11.5 \Rightarrow \sum\limits_{i = 1}^{15} {{x_i} = 172.5} \) (A1)
new mean \(= \frac{{172.5 – 22.1}}{{14}}\) (M1)
= 10.7428… = 10.7 (3sf) A1
\(\frac{{\sum\limits_{i = 1}^{15} {x_i^2} }}{{15}} – {11.5^2} = 9.3\) (M1)
\( \Rightarrow \sum\limits_{i = 1}^{15} {x_i^2 = 2123.25} \)
new variance \(= \frac{{2123.25 – {{22.1}^2}}}{{14}} – {(10.7428…)^2}\) (M1)
= 1.37 (3sf) A1
[6 marks]
Examiners report
Most candidates were successful in finding the correct value of the mean; however, the variance caused many difficulties. Many candidates affirmed that there were no differences in the variance as it remained constant; some others got wrong results due to premature rounding of figures. Many candidates lost the final mark because they rounded their answers prematurely, resulting in a very inaccurate answer to this question.
Question
The marks obtained by a group of students in a class test are shown below.
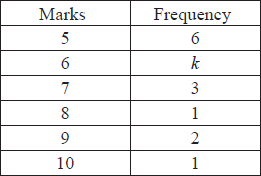
Given the mean of the marks is 6.5, find the value of k.
▶️Answer/Explanation
Markscheme
\(\frac{{5 \times 6 + 6k + 7 \times 3 + 8 \times 1 + 9 \times 2 + 10 \times 1}}{{13 + k}} = 6.5\) (or equivalent) (M1)(A1)(A1)
Note: Award (M1)(A1) for correct numerator, and (A1) for correct denominator.
\(0.5k = 2.5 \Rightarrow k = 5\) A1
[4 marks]
Examiners report
The question was well done generally as one would expect.
Question
Six balls numbered 1, 2, 2, 3, 3, 3 are placed in a bag. Balls are taken one at a time from the bag at random and the number noted. Throughout the question a ball is always replaced before the next ball is taken.
Three balls are taken from the bag. Find the probability that
a.A single ball is taken from the bag. Let \(X\) denote the value shown on the ball.
Find \({\text{E}}(X)\).[2]
b.i.the total of the three numbers is 5;[3]
b.ii.the median of the three numbers is 1.[3]
c.Ten balls are taken from the bag. Find the probability that less than four of the balls are numbered 2.[3]
d.Find the least number of balls that must be taken from the bag for the probability of taking out at least one ball numbered 2 to be greater than 0.95.[3]
e.Another bag also contains balls numbered 1 , 2 or 3.
Eight balls are to be taken from this bag at random. It is calculated that the expected number of balls numbered 1 is 4.8 , and the variance of the number of balls numbered 2 is 1.5.
Find the least possible number of balls numbered 3 in this bag.[8]
▶️Answer/Explanation
Markscheme
\({\text{E}}(X) = 1 \times \frac{1}{6} + 2 \times \frac{2}{6} + 3 \times \frac{3}{6} = \frac{{14}}{6}{\text{ }}\left( { = \frac{7}{3} = 2.33} \right)\) (M1)A1
[2 marks]
\(3 \times {\text{P}}(113) + 3 \times {\text{P}}(122)\) (M1)
\(3 \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{2} + 3 \times \frac{1}{6} \times \frac{1}{3} \times \frac{1}{3} = \frac{7}{{72}}{\text{ }}( = 0.0972)\) A1
Note: Award M1 for attempt to find at least four of the cases.
[3 marks]
recognising 111 as a possibility \(\left( {{\text{implied by }}\frac{1}{{216}}} \right)\) (M1)
recognising 112 and 113 as possibilities \(\left( {{\text{implied by }}\frac{2}{{216}}{\text{ and }}\frac{3}{{216}}} \right)\) (M1)
seeing the three arrangements of 112 and 113 (M1)
\({\text{P}}(111) + 3 \times {\text{P}}(112) + 3 \times {\text{P}}(113)\)
\( = \frac{1}{{216}} + \frac{6}{{216}} + \frac{9}{{216}} = \frac{{16}}{{216}}{\text{ }}\left( { = \frac{2}{{27}} = 0.0741} \right)\) A1
[3 marks]
let the number of twos be \(X,{\text{ }}X \sim B\left( {10,{\text{ }}\frac{1}{3}} \right)\) (M1)
\({\text{P}}(X < 4) = {\text{P}}(X \leqslant 3) = 0.559\) (M1)A1
[3 marks]
let \(n\) be the number of balls drawn
\({\text{P}}(X \geqslant 1) = 1 – {\text{P}}(X = 0)\) M1
\( = 1 – {\left( {\frac{2}{3}} \right)^n} > 0.95\) M1
\({\left( {\frac{2}{3}} \right)^n} > 0.05\)
\(n = 8\) A1
[3 marks]
\(8{p_1} = 4.8 \Rightarrow {p_1} = \frac{3}{5}\) (M1)A1
\(8{p_2}(1 – {p_2}) = 1.5\) (M1)
\(p_2^2 – {p_2} – 0.1875 = 0\) (M1)
\({p_2} = \frac{1}{4}{\text{ }}\left( {{\text{or }}\frac{3}{4}} \right)\) A1
reject \(\frac{3}{4}\) as it gives a total greater than one
\({\text{P}}(1{\text{ or }}2) = \frac{{17}}{{20}}{\text{ or P}}(3) = \frac{3}{{20}}\) (A1)
recognising LCM as 20 so min total number is 20 (M1)
the least possible number of 3’s is 3 A1
[8 marks]
Examiners report
Part (a) was generally well done, although many candidates lost their way after that.
Candidates had difficulty recognising all the different cases in part (b).
Candidates had difficulty recognising all the different cases in part (b).
Parts (c) and (d) should have been more standard questions, but many were unable to tackle them.
Parts (c) and (d) should have been more standard questions, but many were unable to tackle them.
Part (e) was poorly answered in general.
Question
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let \({\text{P}}(X = n)\) be the probability that Kati obtains her third voucher on the \(n{\text{th}}\) bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that \({\text{P}}(X = n) = \frac{{{n^2} + an + b}}{{2000}} \times {0.9^{n – 3}}\) for \(n \geqslant 3,{\text{ }}n \in \mathbb{N}\).
Kati’s mother goes to the shop and buys \(x\) chocolate bars. She takes the bars home for Kati to open.
a.Show that \({\text{P}}(X = 3) = 0.001\) and \({\text{P}}(X = 4) = 0.0027\).[3]
b.Find the values of the constants \(a\) and \(b\).[5]
c.Deduce that \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{0.9(n – 1)}}{{n – 3}}\) for \(n > 3\).[4]
(ii) State the values of \({m_1}\) and \({m_2}\).[5]
e.Determine the minimum value of \(x\) such that the probability Kati receives at least one free gift is greater than 0.5.[3]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 3) = {(0.1)^3}\) A1
\( = 0.001\) AG
\({\text{P}}(X = 4) = {\text{P}}(VV\bar VV) + {\text{P}}(V\bar VVV) + {\text{P}}(\bar VVVV)\) (M1)
\( = 3 \times {(0.1)^3} \times 0.9\) (or equivalent) A1
\( = 0.0027\) AG
[3 marks]
METHOD 1
attempting to form equations in \(a\) and \(b\) M1
\(\frac{{9 + 3a + b}}{{2000}} = \frac{1}{{1000}}{\text{ }}(3a + b = – 7)\) A1
\(\frac{{16 + 4a + b}}{{2000}} \times \frac{9}{{10}} = \frac{{27}}{{10\,000}}{\text{ }}(4a + b = – 10)\) A1
attempting to solve simultaneously (M1)
\(a = – 3,{\text{ }}b = 2\) A1
METHOD 2
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) M1
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) (M1)A1
\( = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) A1
\(a = – 3,b = 2\) A1
Note: Condone the absence of \({0.9^{n – 3}}\) in the determination of the values of \(a\) and \(b\).
[5 marks]
METHOD 1
EITHER
\({\text{P}}(X = n) = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) (M1)
OR
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) (M1)
THEN
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) A1
\({\text{P}}(X = n – 1) = \frac{{(n – 2)(n – 3)}}{{2000}} \times {0.9^{n – 4}}\) A1
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{(n – 1)(n – 2)}}{{(n – 2)(n – 3)}} \times 0.9\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
METHOD 2
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{\frac{{{n^2} – 3n + 2}}{{2000}} \times {{0.9}^{n – 3}}}}{{\frac{{{{(n – 1)}^2} – 3(n – 1) + 2}}{{2000}} \times {{0.9}^{n – 4}}}}\) (M1)
\( = \frac{{0.9({n^2} – 3n + 2)}}{{({n^2} – 5n + 6)}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{0.9(n – 1)(n – 2)}}{{(n – 2)(n – 3)}}\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
[4 marks]
(i) attempting to solve \(\frac{{0.9(n – 1)}}{{n – 3}} = 1\) for \(n\) M1
\(n = 21\) A1
\(\frac{{0.9(n – 1)}}{{n – 3}} < 1 \Rightarrow n > 21\) R1
\(\frac{{0.9(n – 1)}}{{n – 3}} > 1 \Rightarrow n < 21\) R1
\(X\) has two modes AG
Note: Award R1R1 for a clearly labelled graphical representation of the two inequalities (using \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}}\)).
(ii) the modes are 20 and 21 A1
[5 marks]
METHOD 1
\(Y \sim {\text{B}}(x,{\text{ }}0.1)\) (A1)
attempting to solve \({\text{P}}(Y \geqslant 3) > 0.5\) (or equivalent eg \(1 – {\text{P}}(Y \leqslant 2) > 0.5\)) for \(x\) (M1)
Note: Award (M1) for attempting to solve an equality (obtaining \(x = 26.4\)).
\(x = 27\) A1
METHOD 2
\(\sum\limits_{n = 0}^x {{\text{P}}(X = n) > 0.5} \) (A1)
attempting to solve for \(x\) (M1)
\(x = 27\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
