Question: [Maximum mark: 4]
The number of hours spent exercising each week by a group of students is shown in the following table.
| Exercising time (in hours) | Number of students |
| 2 | 5 |
| 3 | 1 |
| 4 | 4 |
| 5 | 3 |
| 6 | x |
The median is 4.5 hours.
(a) Find the value of x .
(b) Find the standard deviation.
▶️Answer/Explanation
Ans:
(a) EITHER
recognising that half the total frequency is 10 (may be seen in an ordered list or indicated on the frequency table)
OR
5 + 1 + 4 = 3 + x
OR
\(\sum f = 20\)
THEN
x = 7
(b) METHOD 1
1.58429…
1.58
METHOD 2
EITHER
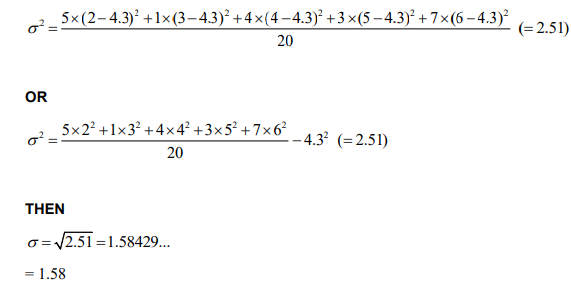
Question
The box and whisker plot below illustrates the IB grades obtained by 100 students.
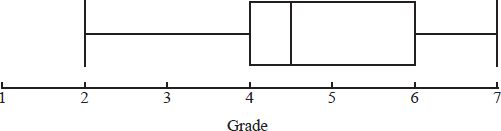
IB grades can only take integer values.
a.How many students obtained a grade of more than 4?[1]
b.State, with reasons, the maximum possible number and minimum possible number of students who obtained a 4 in the exam.[4]
▶️Answer/Explanation
Markscheme
50 A1
[1 mark]
Lower quartile is 4 so at least 26 obtained a 4 R1
Lower bound is 26 A1
Minimum is 2 but the rest could be 4 R1
So upper bound is 49 A1
Note: Do not allow follow through for A marks.
Note: If answers are incorrect award R0A0; if argument is correct but no clear lower/upper bound is stated award R1A0; award R0A1 for correct answer without explanation or incorrect explanation.
[4 marks]
Question
Six balls numbered 1, 2, 2, 3, 3, 3 are placed in a bag. Balls are taken one at a time from the bag at random and the number noted. Throughout the question a ball is always replaced before the next ball is taken.
Three balls are taken from the bag. Find the probability that
A single ball is taken from the bag. Let \(X\) denote the value shown on the ball.
a.Find \({\text{E}}(X)\).[2]
b.i.the total of the three numbers is 5;[3]
b.ii.the median of the three numbers is 1.[3]
c.Ten balls are taken from the bag. Find the probability that less than four of the balls are numbered 2.[3]
d.Find the least number of balls that must be taken from the bag for the probability of taking out at least one ball numbered 2 to be greater than 0.95.[3]
e.Another bag also contains balls numbered 1 , 2 or 3.
Eight balls are to be taken from this bag at random. It is calculated that the expected number of balls numbered 1 is 4.8 , and the variance of the number of balls numbered 2 is 1.5.
Find the least possible number of balls numbered 3 in this bag.[8]
▶️Answer/Explanation
Markscheme
\({\text{E}}(X) = 1 \times \frac{1}{6} + 2 \times \frac{2}{6} + 3 \times \frac{3}{6} = \frac{{14}}{6}{\text{ }}\left( { = \frac{7}{3} = 2.33} \right)\) (M1)A1
[2 marks]
\(3 \times {\text{P}}(113) + 3 \times {\text{P}}(122)\) (M1)
\(3 \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{2} + 3 \times \frac{1}{6} \times \frac{1}{3} \times \frac{1}{3} = \frac{7}{{72}}{\text{ }}( = 0.0972)\) A1
Note: Award M1 for attempt to find at least four of the cases.
[3 marks]
recognising 111 as a possibility \(\left( {{\text{implied by }}\frac{1}{{216}}} \right)\) (M1)
recognising 112 and 113 as possibilities \(\left( {{\text{implied by }}\frac{2}{{216}}{\text{ and }}\frac{3}{{216}}} \right)\) (M1)
seeing the three arrangements of 112 and 113 (M1)
\({\text{P}}(111) + 3 \times {\text{P}}(112) + 3 \times {\text{P}}(113)\)
\( = \frac{1}{{216}} + \frac{6}{{216}} + \frac{9}{{216}} = \frac{{16}}{{216}}{\text{ }}\left( { = \frac{2}{{27}} = 0.0741} \right)\) A1
[3 marks]
let the number of twos be \(X,{\text{ }}X \sim B\left( {10,{\text{ }}\frac{1}{3}} \right)\) (M1)
\({\text{P}}(X < 4) = {\text{P}}(X \leqslant 3) = 0.559\) (M1)A1
[3 marks]
let \(n\) be the number of balls drawn
\({\text{P}}(X \geqslant 1) = 1 – {\text{P}}(X = 0)\) M1
\( = 1 – {\left( {\frac{2}{3}} \right)^n} > 0.95\) M1
\({\left( {\frac{2}{3}} \right)^n} > 0.05\)
\(n = 8\) A1
[3 marks]
\(8{p_1} = 4.8 \Rightarrow {p_1} = \frac{3}{5}\) (M1)A1
\(8{p_2}(1 – {p_2}) = 1.5\) (M1)
\(p_2^2 – {p_2} – 0.1875 = 0\) (M1)
\({p_2} = \frac{1}{4}{\text{ }}\left( {{\text{or }}\frac{3}{4}} \right)\) A1
reject \(\frac{3}{4}\) as it gives a total greater than one
\({\text{P}}(1{\text{ or }}2) = \frac{{17}}{{20}}{\text{ or P}}(3) = \frac{3}{{20}}\) (A1)
recognising LCM as 20 so min total number is 20 (M1)
the least possible number of 3’s is 3 A1
[8 marks]
Question
Six balls numbered 1, 2, 2, 3, 3, 3 are placed in a bag. Balls are taken one at a time from the bag at random and the number noted. Throughout the question a ball is always replaced before the next ball is taken.
Three balls are taken from the bag. Find the probability that
A single ball is taken from the bag. Let \(X\) denote the value shown on the ball.
a.Find \({\text{E}}(X)\).[2]
b.i.the total of the three numbers is 5;[3]
b.ii.the median of the three numbers is 1.[3]
c.Ten balls are taken from the bag. Find the probability that less than four of the balls are numbered 2.[3]
d.Find the least number of balls that must be taken from the bag for the probability of taking out at least one ball numbered 2 to be greater than 0.95.[3]
e.Another bag also contains balls numbered 1 , 2 or 3.
Eight balls are to be taken from this bag at random. It is calculated that the expected number of balls numbered 1 is 4.8 , and the variance of the number of balls numbered 2 is 1.5.
Find the least possible number of balls numbered 3 in this bag.[8]
▶️Answer/Explanation
Markscheme
\({\text{E}}(X) = 1 \times \frac{1}{6} + 2 \times \frac{2}{6} + 3 \times \frac{3}{6} = \frac{{14}}{6}{\text{ }}\left( { = \frac{7}{3} = 2.33} \right)\) (M1)A1
[2 marks]
\(3 \times {\text{P}}(113) + 3 \times {\text{P}}(122)\) (M1)
\(3 \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{2} + 3 \times \frac{1}{6} \times \frac{1}{3} \times \frac{1}{3} = \frac{7}{{72}}{\text{ }}( = 0.0972)\) A1
Note: Award M1 for attempt to find at least four of the cases.
[3 marks]
recognising 111 as a possibility \(\left( {{\text{implied by }}\frac{1}{{216}}} \right)\) (M1)
recognising 112 and 113 as possibilities \(\left( {{\text{implied by }}\frac{2}{{216}}{\text{ and }}\frac{3}{{216}}} \right)\) (M1)
seeing the three arrangements of 112 and 113 (M1)
\({\text{P}}(111) + 3 \times {\text{P}}(112) + 3 \times {\text{P}}(113)\)
\( = \frac{1}{{216}} + \frac{6}{{216}} + \frac{9}{{216}} = \frac{{16}}{{216}}{\text{ }}\left( { = \frac{2}{{27}} = 0.0741} \right)\) A1
[3 marks]
let the number of twos be \(X,{\text{ }}X \sim B\left( {10,{\text{ }}\frac{1}{3}} \right)\) (M1)
\({\text{P}}(X < 4) = {\text{P}}(X \leqslant 3) = 0.559\) (M1)A1
[3 marks]
let \(n\) be the number of balls drawn
\({\text{P}}(X \geqslant 1) = 1 – {\text{P}}(X = 0)\) M1
\( = 1 – {\left( {\frac{2}{3}} \right)^n} > 0.95\) M1
\({\left( {\frac{2}{3}} \right)^n} > 0.05\)
\(n = 8\) A1
[3 marks]
\(8{p_1} = 4.8 \Rightarrow {p_1} = \frac{3}{5}\) (M1)A1
\(8{p_2}(1 – {p_2}) = 1.5\) (M1)
\(p_2^2 – {p_2} – 0.1875 = 0\) (M1)
\({p_2} = \frac{1}{4}{\text{ }}\left( {{\text{or }}\frac{3}{4}} \right)\) A1
reject \(\frac{3}{4}\) as it gives a total greater than one
\({\text{P}}(1{\text{ or }}2) = \frac{{17}}{{20}}{\text{ or P}}(3) = \frac{3}{{20}}\) (A1)
recognising LCM as 20 so min total number is 20 (M1)
the least possible number of 3’s is 3 A1
[8 marks]
Question
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let \({\text{P}}(X = n)\) be the probability that Kati obtains her third voucher on the \(n{\text{th}}\) bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that \({\text{P}}(X = n) = \frac{{{n^2} + an + b}}{{2000}} \times {0.9^{n – 3}}\) for \(n \geqslant 3,{\text{ }}n \in \mathbb{N}\).
Kati’s mother goes to the shop and buys \(x\) chocolate bars. She takes the bars home for Kati to open.
a.Show that \({\text{P}}(X = 3) = 0.001\) and \({\text{P}}(X = 4) = 0.0027\).[3]
b.Find the values of the constants \(a\) and \(b\).[5]
c.Deduce that \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{0.9(n – 1)}}{{n – 3}}\) for \(n > 3\).[4]
d.(i) Hence show that \(X\) has two modes \({m_1}\) and \({m_2}\).
(ii) State the values of \({m_1}\) and \({m_2}\).[5]
e.Determine the minimum value of \(x\) such that the probability Kati receives at least one free gift is greater than 0.5.[3]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 3) = {(0.1)^3}\) A1
\( = 0.001\) AG
\({\text{P}}(X = 4) = {\text{P}}(VV\bar VV) + {\text{P}}(V\bar VVV) + {\text{P}}(\bar VVVV)\) (M1)
\( = 3 \times {(0.1)^3} \times 0.9\) (or equivalent) A1
\( = 0.0027\) AG
[3 marks]
METHOD 1
attempting to form equations in \(a\) and \(b\) M1
\(\frac{{9 + 3a + b}}{{2000}} = \frac{1}{{1000}}{\text{ }}(3a + b = – 7)\) A1
\(\frac{{16 + 4a + b}}{{2000}} \times \frac{9}{{10}} = \frac{{27}}{{10\,000}}{\text{ }}(4a + b = – 10)\) A1
attempting to solve simultaneously (M1)
\(a = – 3,{\text{ }}b = 2\) A1
METHOD 2
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) M1
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) (M1)A1
\( = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) A1
\(a = – 3,b = 2\) A1
Note: Condone the absence of \({0.9^{n – 3}}\) in the determination of the values of \(a\) and \(b\).
[5 marks]
METHOD 1
EITHER
\({\text{P}}(X = n) = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) (M1)
OR
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) (M1)
THEN
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) A1
\({\text{P}}(X = n – 1) = \frac{{(n – 2)(n – 3)}}{{2000}} \times {0.9^{n – 4}}\) A1
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{(n – 1)(n – 2)}}{{(n – 2)(n – 3)}} \times 0.9\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
METHOD 2
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{\frac{{{n^2} – 3n + 2}}{{2000}} \times {{0.9}^{n – 3}}}}{{\frac{{{{(n – 1)}^2} – 3(n – 1) + 2}}{{2000}} \times {{0.9}^{n – 4}}}}\) (M1)
\( = \frac{{0.9({n^2} – 3n + 2)}}{{({n^2} – 5n + 6)}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{0.9(n – 1)(n – 2)}}{{(n – 2)(n – 3)}}\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
[4 marks]
(i) attempting to solve \(\frac{{0.9(n – 1)}}{{n – 3}} = 1\) for \(n\) M1
\(n = 21\) A1
\(\frac{{0.9(n – 1)}}{{n – 3}} < 1 \Rightarrow n > 21\) R1
\(\frac{{0.9(n – 1)}}{{n – 3}} > 1 \Rightarrow n < 21\) R1
\(X\) has two modes AG
Note: Award R1R1 for a clearly labelled graphical representation of the two inequalities (using \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}}\)).
(ii) the modes are 20 and 21 A1
[5 marks]
METHOD 1
\(Y \sim {\text{B}}(x,{\text{ }}0.1)\) (A1)
attempting to solve \({\text{P}}(Y \geqslant 3) > 0.5\) (or equivalent eg \(1 – {\text{P}}(Y \leqslant 2) > 0.5\)) for \(x\) (M1)
Note: Award (M1) for attempting to solve an equality (obtaining \(x = 26.4\)).
\(x = 27\) A1
METHOD 2
\(\sum\limits_{n = 0}^x {{\text{P}}(X = n) > 0.5} \) (A1)
attempting to solve for \(x\) (M1)
\(x = 27\) A1
[3 marks]
