Question
A biased coin is weighted such that the probability of obtaining a head is \(\frac{4}{7}\). The coin is tossed 6 times and X denotes the number of heads observed. Find the value of the ratio \(\frac{{{\text{P}}(X = 3)}}{{{\text{P}}(X = 2)}}\).
▶️Answer/Explanation
Markscheme
recognition of \(X \sim {\text{B}}\left( {6,\frac{4}{7}} \right)\) (M1)
\({\text{P}}(X = 3) = \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right){\left( {\frac{4}{7}} \right)^3}{\left( {\frac{3}{7}} \right)^3}\left( { = 20 \times \frac{{{4^3} \times {3^3}}}{{{7^6}}}} \right)\) A1
\({\text{P}}(X = 2) = \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right){\left( {\frac{4}{7}} \right)^2}{\left( {\frac{3}{7}} \right)^4}\left( { = 15 \times \frac{{{4^2} \times 34}}{{{7^6}}}} \right)\) A1
\(\frac{{{\text{P}}(X = 3)}}{{{\text{P}}(X = 2)}} = \frac{{80}}{{45}}\left( { = \frac{{16}}{9}} \right)\) A1
[4 marks]
Examiners report
Many correct answers were seen to this and the majority of candidates recognised the need to use a Binomial distribution. A number of candidates, although finding the correct expressions for \({\text{P}}(X = 3)\) and \({\text{P}}(X = 4)\), were unable to perform the required simplification.
Question
On Saturday, Alfred and Beatrice play 6 different games against each other. In each game, one of the two wins. The probability that Alfred wins any one of these games is \(\frac{2}{3}\).
Show that the probability that Alfred wins exactly 4 of the games is \(\frac{{80}}{{243}}\).
(i) Explain why the total number of possible outcomes for the results of the 6 games is 64.
(ii) By expanding \({(1 + x)^6}\) and choosing a suitable value for x, prove
\[64 = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)\]
(iii) State the meaning of this equality in the context of the 6 games played.
The following day Alfred and Beatrice play the 6 games again. Assume that the probability that Alfred wins any one of these games is still \(\frac{2}{3}\).
(i) Find an expression for the probability Alfred wins 4 games on the first day and 2 on the second day. Give your answer in the form \({\left( {\begin{array}{*{20}{c}}
6 \\
r
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^s}{\left( {\frac{1}{3}} \right)^t}\) where the values of r, s and t are to be found.
(ii) Using your answer to (c) (i) and 6 similar expressions write down the probability that Alfred wins a total of 6 games over the two days as the sum of 7 probabilities.
(iii) Hence prove that \(\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right) = {\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2}\).
Alfred and Beatrice play n games. Let A denote the number of games Alfred wins. The expected value of A can be written as \({\text{E}}(A) = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{a^r}}}{{{b^n}}}\).
(i) Find the values of a and b.
(ii) By differentiating the expansion of \({(1 + x)^n}\), prove that the expected number of games Alfred wins is \(\frac{{2n}}{3}\).
▶️Answer/Explanation
Markscheme
\(B\left( {6,\frac{2}{3}} \right)\) (M1)
\(p(4) = \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right){\left( {\frac{2}{3}} \right)^4}{\left( {\frac{1}{3}} \right)^2}\) A1
\(\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) = 15\) A1
\( = 15 \times \frac{{{2^4}}}{{{3^6}}} = \frac{{80}}{{243}}\) AG
[3 marks]
(i) 2 outcomes for each of the 6 games or \({2^6} = 64\) R1
(ii) \({(1 + x)^6} = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)x + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right){x^2} + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right){x^3} + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right){x^4} + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right){x^5} + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right){x^6}\) A1
Note: Accept \(^n{C_r}\) notation or \(1 + 6x + 15{x^2} + 20{x^3} + 15{x^4} + 6{x^5} + {x^6}\)
setting x = 1 in both sides of the expression R1
Note: Do not award R1 if the right hand side is not in the correct form.
\(64 = \left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)\) AG
(iii) the total number of outcomes = number of ways Alfred can win no games, plus the number of ways he can win one game etc. R1
[4 marks]
(i) Let \({\text{P}}(x,{\text{ }}y)\) be the probability that Alfred wins x games on the first day and y on the second.
\({\text{P(4, 2)}} = \left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^4} \times {\left( {\frac{1}{3}} \right)^2} \times \left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^2} \times {\left( {\frac{1}{3}} \right)^4}\) M1A1
\({\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) or \({\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) A1
r = 2 or 4, s = t = 6
(ii) P(Total = 6) =
P(0, 6) + P(1, 5) + P(2, 4) + P(3, 3) + P(4, 2) + P(5, 1) + P(6, 0) (M1)
\( = {\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6} + … + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2}{\left( {\frac{2}{3}} \right)^6}{\left( {\frac{1}{3}} \right)^6}\) A2
\( = \frac{{{2^6}}}{{{3^{12}}}}\left( {{{\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)}^2}} \right)\)
Note: Accept any valid sum of 7 probabilities.
(iii) use of \(\left( {\begin{array}{*{20}{c}}
6 \\
i
\end{array}} \right) = \left( {\begin{array}{*{20}{l}}
6 \\
{6 – i}
\end{array}} \right)\) (M1)
(can be used either here or in (c)(ii))
P(wins 6 out of 12) \( = \left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right) \times {\left( {\frac{2}{3}} \right)^6} \times {\left( {\frac{1}{3}} \right)^6} = \frac{{{2^6}}}{{{3^{12}}}}\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) A1
\( = \frac{{{2^6}}}{{{3^{12}}}}\left( {{{\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)}^2} + {{\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)}^2}} \right) = \frac{{{2^6}}}{{{3^{12}}}}\left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) A1
therefore \({\left( {\begin{array}{*{20}{c}}
6 \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
2
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
3
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
4
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
5
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
6 \\
6
\end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}}
{12} \\
6
\end{array}} \right)\) AG
[9 marks]
(i) \({\text{E}}(A) = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} {\left( {\frac{2}{3}} \right)^r}{\left( {\frac{1}{3}} \right)^{n – r}} = \sum\limits_{r = 0}^n {r\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{2^r}}}{{{3^n}}}\)
(a = 2, b = 3) M1A1
Note: M0A0 for a = 2, b = 3 without any method.
(ii) \(n{(1 + x)^{n – 1}} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r{x^{r – 1}}\) A1A1
(sigma notation not necessary)
(if sigma notation used also allow lower limit to be r = 0)
let x = 2 M1
\(n{3^{n – 1}} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r{2^{r – 1}}\)
multiply by 2 and divide by \({3^n}\) (M1)
\(\frac{{2n}}{3} = \sum\limits_{r = 1}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} r\frac{{{2^r}}}{{{3^n}}}\left( { = \sum\limits_{r = 0}^n {\left( {\begin{array}{*{20}{c}}
n \\
r
\end{array}} \right)} \frac{{{2^r}}}{{{3^n}}}} \right)\) AG
[6 marks]
Examiners report
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(a) Candidates need to be aware how to work out binomial coefficients without a calculator
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(b) (ii) A surprising number of candidates chose to work out the values of all the binomial coefficients (or use Pascal’s triangle) to make a total of 64 rather than simply putting 1 into the left hand side of the expression.
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
This question linked the binomial distribution with binomial expansion and coefficients and was generally well done.
(d) This was poorly done. Candidates were not able to manipulate expressions given using sigma notation.
Question
A biased coin is tossed five times. The probability of obtaining a head in any one throw is \(p\).
Let \(X\) be the number of heads obtained.
Find, in terms of \(p\), an expression for \({\text{P}}(X = 4)\).
(i) Determine the value of \(p\) for which \({\text{P}}(X = 4)\) is a maximum.
(ii) For this value of \(p\), determine the expected number of heads.
▶️Answer/Explanation
Markscheme
\(X \sim {\text{B}}(5,{\text{ }}p)\) (M1)
\({\text{P}}(X = 4) = \left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right){p^4}(1 – p)\) (or equivalent) A1
[2 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}p}}(5{p^4} – 5{p^5}) = 20{p^3} – 25{p^4}\) M1A1
\(5{p^3}(4 – 5p) = 0 \Rightarrow p = \frac{4}{5}\) M1A1
Note: Do not award the final A1 if \(p = 0\) is included in the answer.
(ii) \({\text{E}}(X) = np = 5\left( {\frac{4}{5}} \right)\) (M1)
\( = 4\) A1
[6 marks]
Examiners report
This question was generally very well done and posed few problems except for the weakest candidates.
This question was generally very well done and posed few problems except for the weakest candidates.
Question
A biased coin is tossed five times. The probability of obtaining a head in any one throw is \(p\).
Let \(X\) be the number of heads obtained.
Find, in terms of \(p\), an expression for \({\text{P}}(X = 4)\).
(i) Determine the value of \(p\) for which \({\text{P}}(X = 4)\) is a maximum.
(ii) For this value of \(p\), determine the expected number of heads.
▶️Answer/Explanation
Markscheme
\(X \sim {\text{B}}(5,{\text{ }}p)\) (M1)
\({\text{P}}(X = 4) = \left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right){p^4}(1 – p)\) (or equivalent) A1
[2 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}p}}(5{p^4} – 5{p^5}) = 20{p^3} – 25{p^4}\) M1A1
\(5{p^3}(4 – 5p) = 0 \Rightarrow p = \frac{4}{5}\) M1A1
Note: Do not award the final A1 if \(p = 0\) is included in the answer.
(ii) \({\text{E}}(X) = np = 5\left( {\frac{4}{5}} \right)\) (M1)
\( = 4\) A1
[6 marks]
Examiners report
This question was generally very well done and posed few problems except for the weakest candidates.
This question was generally very well done and posed few problems except for the weakest candidates.
Question
Chloe and Selena play a game where each have four cards showing capital letters A, B, C and D.
Chloe lays her cards face up on the table in order A, B, C, D as shown in the following diagram.
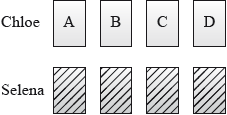
Selena shuffles her cards and lays them face down on the table. She then turns them over one by one to see if her card matches with Chloe’s card directly above.
Chloe wins if no matches occur; otherwise Selena wins.
Chloe and Selena repeat their game so that they play a total of 50 times.
Suppose the discrete random variable X represents the number of times Chloe wins.
Show that the probability that Chloe wins the game is \(\frac{3}{8}\).
Determine the mean of X.
Determine the variance of X.
▶️Answer/Explanation
Markscheme
METHOD 1
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving “no matches” (Chloe winning):
Selena could deal B, C, D (ie, 3 possibilities)
as her first card R1
for each of these matches, there are only 3 possible combinations for the remaining 3 cards R1
so no. ways achieving no matches \( = 3 \times 3 = 9\) M1A1
so probability Chloe wins \( = \frac{9}{{23}} = \frac{3}{8}\) A1AG
METHOD 2
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving a match (Selena winning)
Selena card A can match with Chloe card A, giving 6 possibilities for this happening R1
if Selena deals B as her first card, there are only 3 possible combinations for the remaining 3 cards. Similarly for dealing C and dealing D R1
so no. ways achieving one match is \( = 6 + 3 + 3 + 3 = 15\) M1A1
so probability Chloe wins \( = 1 – \frac{{15}}{{24}} = \frac{3}{8}\) A1AG
METHOD 3
systematic attempt to find number of outcomes where Chloe wins (no matches)
(using tree diag. or otherwise) M1
9 found A1
each has probability \(\frac{1}{4} \times \frac{1}{3} \times \frac{1}{2} \times 1\) M1
\( = \frac{1}{{24}}\) A1
their 9 multiplied by their \(\frac{1}{{24}}\) M1A1
\( = \frac{3}{8}\) AG
[6 marks]
\(X \sim {\text{B}}\left( {50,{\text{ }}\frac{3}{8}} \right)\) (M1)
\(\mu = np = 50 \times \frac{3}{8} = \frac{{150}}{8}{\text{ }}\left( { = \frac{{75}}{4}} \right){\text{ }}( = 18.75)\) (M1)A1
[3 marks]
\({\sigma ^2} = np(1 – p) = 50 \times \frac{3}{8} \times \frac{5}{8} = \frac{{750}}{{64}}{\text{ }}\left( { = \frac{{375}}{{32}}} \right){\text{ }}( = 11.7)\) (M1)A1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
[without GDC]
The random variable \(X\) follows the binomial distribution B(\(n,p\)). Given that \(E(X)\) = \(10\) and Var(\(X\)) = \(6\) find the values of \(n\) and \(p\).
▶️Answer/Explanation
Ans
\(np=10\) and \(np(1-p)=6\). Hence \(10(1-p)=6 \Leftrightarrow \(p=0.4\) and \(n=25\)
Question
[with GDC]
A fair coin is tossed five times. Calculate the probability of obtaining
(a) exactly three heads;
(b) at least one head.
▶️Answer/Explanation
Ans
B\((n,p)\) with \(n= 5\) and \(p= \frac{1}{2}\)
(a) \(P(X = 3) = 0.3125 … = 0.313\)
(b) \(P(X \geq 1) = 0.969\)
Question
[with GDC]
The probability of obtaining heads on a biased coin is \(0.18\). The coin is tossed seven times.
(a) Find the probability of obtaining exactly two heads.
(b) Find the probability of obtaining at least two heads.
▶️Answer/Explanation
Ans
\(B( n, p)\) with \(n = 7\) and \(p = 0.18\)
(a) \(P(X = 2) = 0.252\)
(b) \(P(X \geq 2) = 0.368\)
Question
[with GDC]
A factory makes switches. The probability that a switch is defective is \(0.04\).
The factory tests a random sample of \(100\) switches.
(a) Find the mean number of defective switches in the sample.
(b) Find the probability that there are exactly six defective switches in the sample.
(c) Find the probability that there is at least one defective switch in the sample.
▶️Answer/Explanation
Ans
\(B( n,p)\) with \(n = 100\) and \(p = 0.04\)
(a) mean = \(np = 100\) \times \(0.04 = 4\)
(b) \(P(X = 6)\) = \(0.105\)
(c) \(P(X \geq 1) = 0.983\)
Question
[with GDC]
A factory makes calculators. Over a long period, \(2\)% of them are found to be faulty. A random sample of \(100\) calculators is tested.
(a) Write down the expected number of faulty calculators in the sample.
(b) Find the probability that three calculators are faulty.
(c) Find the probability that more than one calculator is faulty.
▶️Answer/Explanation
Ans
\(X \sim B(100,0.02)\)
(a) \(E(X) = 100 \times 0.02 = 2\)
(b) (i) \(P(X = 3) = 0.182\) (ii) \(P(X > 1) = 0.597\)
Question
[with GDC]
A box contains \(35\) red discs and \(5\) black discs. A disc is selected at random and its colour noted. The disc is then replaced in the box.
(a) In eight such selections, what is the probability that a black disc is selected
(i) exactly once?
(ii) at least once?
(b) The process of selecting and replacing is carried out \(400\) times.
What is the expected number of black discs that would be drawn?
▶️Answer/Explanation
Ans
\(p\)(Red)=\(\frac{35}{40}=\frac{7}{8}\) \(p\)(Black)=\(\frac{5}{40}=\frac{1}{8}\)
(a) B( n, p ) with n = 5, p=\(\frac{1}{8}\)
(i) \(p\)(one black) = P(\(X = 1) = 0.393\) to \(3\) s.f.
(ii) \(p\)(at least one black) = \(P(X\geq 1)=0.656\)
(b) 400 draws: expected number of blacks =\(\frac{400}{8}=50\)
Question
[with GDC]
The probability of obtaining heads on a biased coin is \(\frac{1}{3}\)
(a) Sammy tosses the coin three times. Find the probability of getting
(i) three heads;
(ii) two heads and one tail.
(b) Amir plays a game in which he tosses the coin \(12\) times.
(i) Find the expected number of heads.
(ii) Amir wins \($10\) for each head obtained and loses \($6\) for each tail. Find his expected winnings.
▶️Answer/Explanation
Ans
(a) B\((n, p)\) with \(n=3, p=\frac{1}{3}\)
(i) \(P(X = 3) = 0.0370\) or P(\(3\)H)= \(\left ( \frac{1}{3}^{3} \right )=\frac{1}{27}\)
(ii) \(P(X = 3) = 0.222\) or P(2H, 1T) = \(3\left ( \frac{1}{3}^{2} \right )\frac{2}{3}=\frac{2}{9}\)
(b) (i) expected number of heads = \(np\) = \(\left ( \frac{1}{3}\times 12 \right )=4\)
(ii) \(4\) heads, so \(8\) tails
E(winnings) = \(4\times 10-8\times 6(=40-48)\)= \(–$ 8\)
Question
[without GDC]
Two fair four-sided dice, one red and one green, are thrown. For each die, the faces are labelled 1, 2, 3, 4. The score for each die is the number which lands face down.
The sample space is shown below:
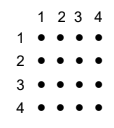
(a) Write down the probability that two scores of \(4\) are obtained.
Let \(X\) be the number of \(4\)s that land face down.
(b) Complete the following probability distribution for \(X\).

(c) Find \(E(X)\).
Chris plays a game where he rolls the dice above. If two \(4\)s are obtained he wins \(20\)€.
If only one \(4\) is obtained he wins \(5\)€. If no \(4\) is obtained he loses \(2\)€
(d) Find the expected amount earned in one game.
(e) If Chris plays this game \(100\) times find the amount he is expected to win.
▶️Answer/Explanation
Ans
(a) Probability of two \(4\)s is \(\frac{1}{16}(=0.0625)\)
(b) 
(c) \(E(X)=\sum_{0}^{2} xP(X=x),=0\times \frac{9}{16}+1\times \frac{6}{16}+2\times \frac{1}{16}\frac{8}{16}\left ( =\frac{1}{2} \right )\)
or \(E(X)=np=2\times \frac{1}{4}=\frac{1}{2}\)
(d) 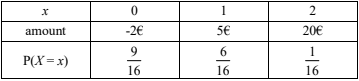
Expected amount = \(-2\times \frac{9}{16}+5\times \frac{6}{16}+20\times \frac{1}{16}= 2\)€
(e) \(100\times 2\)= \(200\) €
Question
[with GDC]
Bag A contains \(2\) red balls and \(3\) green balls. Two balls are chosen at random from the bag without replacement. Let \(X\) denote the number of red balls chosen. The following
table shows the probability distribution for \(X\)

(a) Calculate E(X), the mean number of red balls chosen.
Bag B contains \(4\) red balls and \(2\) green balls. Two balls are chosen at random from bag B.
(b) (i) Draw a tree diagram to represent the above information, including the probability of each event.
(ii) Hence find the probability distribution for \(Y\), where \(Y\) is the number of red balls chosen.
A standard die with six faces is rolled. If a \(1\) or \(6\) is obtained, two balls are chosen from bag A, otherwise two balls are chosen from bag B.
(c) Calculate the probability that two red balls are chosen.
(d) Given that two red balls are obtained, find the conditional probability that a \(1\) or \(6\) was rolled on the die.
▶️Answer/Explanation
Ans
(a) \(E(X)=0\times \frac{3}{10}+1\times \frac{6}{10}+2\times \frac{1}{10}=\frac{8}{10} (0.8)\)
(b) (i) 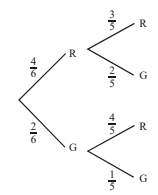
(ii) \(P(Y=0)=\frac{2}{5}\times \frac{1}{5}=\frac{2}{30}\)
\(P(Y=1)= P(RG)+P(GR \left ( =\frac{4}{6}\times \frac{2}{5}+\frac{2}{6}\times \frac{4}{5} \right )=\frac{16}{30}\)
\(P(Y=2)= \frac{4}{6}\times \frac{3}{5}=\frac{12}{30}\)
Forming a distribution
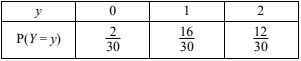
(c) \(P(RR)=\frac{1}{3}\times \frac{1}{10}+\frac{2}{3}\times \frac{12}{30}=\frac{27}{90} \left ( \frac{3}{10}, 0.3 \right )\)
(d) \(P(1 or 6|RR)= P(A|RR)= \frac{P(A\cap RR)}{P(RR)}=\frac{1}{30}\div \frac{27}{90}=\frac{3}{27} \left ( \frac{1}{9},0.111 \right )\)
Question
[without GDC]
A four-sided die has three blue faces and one red face. The die is rolled. Let \(B\) be the event a blue face lands down, and \(R\) be the event a red face lands down.
(a) Write down the values of
(i) \(P(B)\)
(ii) \(P(R)\)
(b) If the blue face lands down, the die is not rolled again. If the red face lands down, the die is rolled once again. This is represented by the following tree diagram, where \(p, s, t\) are
probabilities.
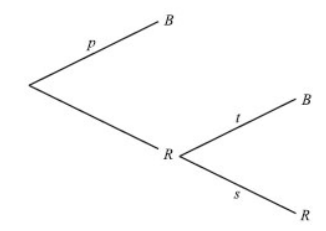
Find the value of \(p\), of \(s\) and of \(t\).
Guiseppi plays a game where he rolls the die. If a blue face lands down, he scores \(2\) and is finished. If the red face lands down, he scores \(1\) and rolls one more time. Let \(X\) be the total score obtained.
(c) (i) Show that \(P(X=3)=\frac{3}{16}\).
(ii) Find P \((X = 2)\).
(d) (i) Construct a probability distribution table for \(X\).
(ii) Calculate the expected value of \(X\).
(e) If the total score is \(3\), Guiseppi wins \($10\). If the total score is \(2\), Guiseppi gets nothing. He plays the game twice. Find the probability that he wins exactly \($10\).
▶️Answer/Explanation
Ans
(a) (i) P\((B)=\frac{3}{4} \) (ii) P\((R)=\frac{1}{4}\)
(b) \(p=\frac{3}{4}\ s=\frac{1}{4},\ t=\frac{3}{4}\)
(c) (i) \(P(X=3)\)=P(getting \(1\) and \(2\))=\(\frac{1}{4}\times \frac{3}{4}=\frac{3}{16}\)
(ii) \(P(X=2)=\frac{1}{4}\times \frac{1}{4}+\frac{3}{4} \left ( or\ 1-\frac{3}{16} \right )= \frac{13}{16}\)
(d) (i) 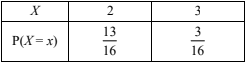
(ii) \(E(X)= 2\left ( \frac{13}{16} \right )+3\left ( \frac{3}{16} \right )=\frac{35}{16}\)
(e) win \($10 \Rightarrow\) scores \(3\) one time, \(2\) other time
P(win \($10\)) = \(P(3)\times P(2)+P(2)\times P(3)=2\left ( \frac{13}{16}\times \frac{3}{16} \right ), =\frac{78}{256}\left ( =\frac{39}{128} \right )\)
Question
[with GDC]
A pair of fair dice is thrown.
(a) Complete the tree diagram below, which shows the possible outcomes.
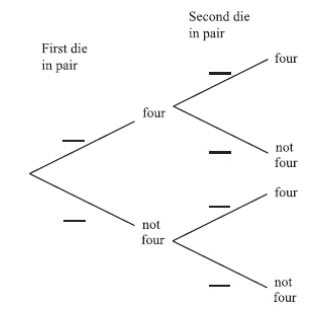
Let \(E\) be the event that exactly one four occurs when the pair of dice is thrown.
(b) Calculate \(P(E)\).
The pair of dice is now thrown five times.
(c) Calculate the probability that event \(E\) occurs exactly three times in the five throws.
(d) Calculate the probability that event \(E\) occurs at least three times in the five throws.
▶️Answer/Explanation
Ans
(a) 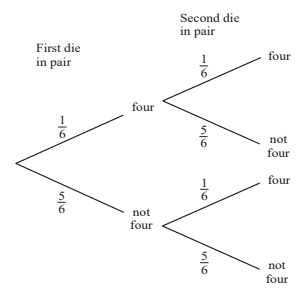
(b) \(P(E)=\frac{1}{6}\times \frac{5}{6}+\frac{5}{6}\times \frac{1}{6} \left ( =\frac{5}{36}+\frac{5}{36} \right )=\frac{10}{36} \left ( \frac{5}{18}\ or\ 0.0278\right )\)
(c) \(X\sim B \left ( 5, \frac{5}{18} \right )\)
P\((X=3)=0.112\) [in fact \(\binom{5}{3}\left ( \frac{5}{3} \right )^{3}\left ( \frac{13}{8} \right )^{2}=0.112\)]
(d) \(P(X\geq 3)=0.135\)
