Question
Consider the function \(f(x) = \frac{{\ln x}}{x}\) , \(0 < x < {{\text{e}}^2}\) .
(i) Solve the equation \(f'(x) = 0\) .
(ii) Hence show the graph of \(f\) has a local maximum.
(iii) Write down the range of the function \(f\) .[5]
Show that there is a point of inflexion on the graph and determine its coordinates.[5]
Sketch the graph of \(y = f(x)\) , indicating clearly the asymptote, x-intercept and the local maximum.[3]
Now consider the functions \(g(x) = \frac{{\ln \left| x \right|}}{x}\) and \(h(x) = \frac{{\ln \left| x \right|}}{{\left| x \right|}}\) , where \(0 < x < {{\text{e}}^2}\) .
(i) Sketch the graph of \(y = g(x)\) .
(ii) Write down the range of \(g\) .
(iii) Find the values of \(x\) such that \(h(x) > g(x)\) .[6]
Answer/Explanation
Markscheme
(i) \(f'(x) = \frac{{x\frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\)
so \(f'(x) = 0\) when \(\ln x = 1\), i.e. \(x = {\text{e}}\) A1
(ii) \(f'(x) > 0\) when \(x < {\text{e}}\) and \(f'(x) < 0\) when \(x > {\text{e}}\) R1
hence local maximum AG
Note: Accept argument using correct second derivative.
(iii) \(y \leqslant \frac{1}{{\text{e}}}\) A1
[5 marks]
\(f”(x) = \frac{{{x^2}\frac{{ – 1}}{x} – \left( {1 – \ln x} \right)2x}}{{{x^4}}}\) M1
\( = \frac{{ – x – 2x + 2x\ln x}}{{{x^4}}}\)
\( = \frac{{ – 3 + 2\ln x}}{{{x^3}}}\) A1
Note: May be seen in part (a).
\(f”(x) = 0\) (M1)
\({ – 3 + 2\ln x = 0}\)
\(x = {{\text{e}}^{\frac{3}{2}}}\)
since \(f”(x) < 0\) when \(x < {{\text{e}}^{\frac{3}{2}}}\) and \(f”(x) > 0\) when \(x > {{\text{e}}^{\frac{3}{2}}}\) R1
then point of inflexion \(\left( {{{\text{e}}^{\frac{3}{2}}},\frac{3}{{2{{\text{e}}^{\frac{3}{2}}}}}} \right)\) A1
[5 marks]
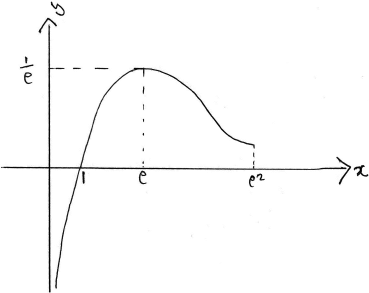A1A1A1
Note: Award A1 for the maximum and intercept, A1 for a vertical asymptote and A1 for shape (including turning concave up).
[3 marks]
(i)
A1A1
Note: Award A1 for each correct branch.
(ii) all real values A1
(iii)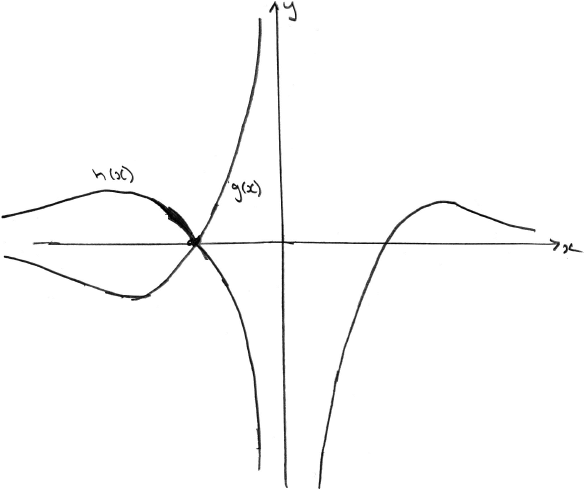
(M1)(A1)
Note: Award (M1)(A1) for sketching the graph of h, ignoring any graph of g.
\( – {{\text{e}}^2} < x < – 1\) (accept \(x < – 1\) ) A1
[6 marks]
Question
Let \(f(x) = \sqrt {\frac{x}{{1 – x}}} ,{\text{ }}0 < x < 1\).
Show that \(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) and deduce that f is an increasing function.[5]
Show that the curve \(y = f(x)\) has one point of inflexion, and find its coordinates.[6]
Use the substitution \(x = {\sin ^2}\theta \) to show that \(\int {f(x){\text{d}}x} = \arcsin \sqrt x – \sqrt {x – {x^2}} + c\) .[11]
Answer/Explanation
Markscheme
EITHER
derivative of \(\frac{x}{{1 – x}}\) is \(\frac{{(1 – x) – x( – 1)}}{{{{(1 – x)}^2}}}\) M1A1
\(f'(x) = \frac{1}{2}{\left( {\frac{x}{{1 – x}}} \right)^{ – \frac{1}{2}}}\frac{1}{{{{(1 – x)}^2}}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
OR
\(f(x) = \frac{{{x^{\frac{1}{2}}}}}{{{{(1 – x)}^{\frac{1}{2}}}}}\)
\(f'(x) = \frac{{{{(1 – x)}^{\frac{1}{2}}}\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \frac{1}{2}{x^{\frac{1}{2}}}{{(1 – x)}^{ – \frac{1}{2}}}( – 1)}}{{1 – x}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{1}{2}}} + \frac{1}{2}{x^{\frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}[1 – x + x]\) M1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
[5 marks]
\(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\)
\( \Rightarrow f”(x) = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{3}{2}}} + \frac{3}{4}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{5}{2}}}\) M1A1
\( = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{5}{2}}}[1 – 4x]\)
\(f”(x) = 0 \Rightarrow x = \frac{1}{4}\) M1A1
\(f”(x)\) changes sign at \(x = \frac{1}{4}\) hence there is a point of inflexion R1
\(x = \frac{1}{4} \Rightarrow y = \frac{1}{{\sqrt 3 }}\) A1
the coordinates are \(\left( {\frac{1}{4},\frac{1}{{\sqrt 3 }}} \right)\)
[6 marks]
\(x = {\sin ^2}\theta \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = 2\sin \theta \cos \theta \) M1A1
\(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \int {\sqrt {\frac{{{{\sin }^2}\theta }}{{1 – {{\sin }^2}\theta }}} 2\sin \theta \cos \theta {\text{d}}\theta } } \) M1A1
\( = \int {2{{\sin }^2}\theta {\text{d}}\theta } \) A1
\( = \int {1 – \cos 2\theta } {\text{d}}\theta \) M1A1
\( = \theta – \frac{1}{2}\sin 2\theta + c\) A1
\(\theta = \arcsin \sqrt x \) A1
\(\frac{1}{2}\sin 2\theta = \sin \theta \cos \theta = \sqrt x \sqrt {1 – x} = \sqrt {x – {x^2}} \) M1A1
hence \(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \arcsin \sqrt x } – \sqrt {x – {x^2}} + c\) AG
[11 marks]
Question
Consider the curve defined by the equation \({x^2} + \sin y – xy = 0\) .
Find the gradient of the tangent to the curve at the point \((\pi ,{\text{ }}\pi )\) .[6]
Hence, show that \(\tan \theta = \frac{1}{{1 + 2\pi }}\), where \(\theta \) is the acute angle between the tangent to the curve at \((\pi ,{\text{ }}\pi )\) and the line y = x .[3]
Answer/Explanation
Markscheme
attempt to differentiate implicitly M1
\(2x + \cos y\frac{{{\text{d}}y}}{{{\text{d}}x}} – y – x\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) A1A1
Note: A1 for differentiating \({x^2}\) and sin y ; A1 for differentiating xy.
substitute x and y by \(\pi \) M1
\(2\pi – \frac{{{\text{d}}y}}{{{\text{d}}x}} – \pi – \pi \frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{\pi }{{1 + \pi }}\) M1A1
Note: M1 for attempt to make dy/dx the subject. This could be seen earlier.
[6 marks]
\(\theta = \frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}\) (or seen the other way) M1
\(\tan \theta = \tan \left( {\frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}} \right) = \frac{{1 – \frac{\pi }{{1 + \pi }}}}{{1 + \frac{\pi }{{1 + \pi }}}}\) M1A1
\(\tan \theta = \frac{1}{{1 + 2\pi }}\) AG
[3 marks]
Question
The curve C is given by \(y = \frac{{x\cos x}}{{x + \cos x}}\), for \(x \geqslant 0\).
Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{{\cos }^2}x – {x^2}\sin x}}{{{{(x + \cos x)}^2}}},{\text{ }}x \geqslant 0\).[4]
Find the equation of the tangent to C at the point \(\left( {\frac{\pi }{2},0} \right)\).[3]
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(x + \cos x)(\cos x – x\sin x) – x\cos x(1 – \sin x)}}{{{{(x + \cos x)}^2}}}\) M1A1A1
Note: Award M1 for attempt at differentiation of a quotient and a product condoning sign errors in the quotient formula and the trig differentiations, A1 for correct derivative of “u”, A1 for correct derivative of “v”.
\( = \frac{{x\cos x + {{\cos }^2}x – {x^2}\sin x – x\cos x\sin x – x\cos x + x\cos x\sin x}}{{{{(x + \cos x)}^2}}}\) A1
\( = \frac{{{{\cos }^2}x – {x^2}\sin x}}{{{{(x + \cos x)}^2}}}\) AG
[4 marks]
the derivative has value –1 (A1)
the equation of the tangent line is \((y – 0) = ( – 1)\left( {x – \frac{\pi }{2}} \right)\left( {y = \frac{\pi }{2} – x} \right)\) M1A1
[3 marks]
Question
The function f is defined by \(f(x) = \frac{{2x – 1}}{{x + 2}}\), with domain \(D = \{ x: – 1 \leqslant x \leqslant 8\} \).
Express \(f(x)\) in the form \(A + \frac{B}{{x + 2}}\), where \(A\) and \(B \in \mathbb{Z}\).[2]
Hence show that \(f'(x) > 0\) on D.[2]
State the range of f.[2]
(i) Find an expression for \({f^{ – 1}}(x)\).
(ii) Sketch the graph of \(y = f(x)\), showing the points of intersection with both axes.
(iii) On the same diagram, sketch the graph of \(y = f'(x)\).[8]
(i) On a different diagram, sketch the graph of \(y = f(|x|)\) where \(x \in D\).
(ii) Find all solutions of the equation \(f(|x|) = – \frac{1}{4}\).[7]
Answer/Explanation
Markscheme
by division or otherwise
\(f(x) = 2 – \frac{5}{{x + 2}}\) A1A1
[2 marks]
\(f'(x) = \frac{5}{{{{(x + 2)}^2}}}\) A1
> 0 as \({(x + 2)^2} > 0\) (on D) R1AG
Note: Do not penalise candidates who use the original form of the function to compute its derivative.
[2 marks]
\(S = \left[ { – 3,\frac{3}{2}} \right]\) A2
Note: Award A1A0 for the correct endpoints and an open interval.
[2 marks]
(i) EITHER
rearrange \(y = f(x)\) to make x the subject M1
obtain one-line equation, e.g. \(2x – 1 = xy + 2y\) A1
\(x = \frac{{2y + 1}}{{2 – y}}\) A1
OR
interchange x and y M1
obtain one-line equation, e.g. \(2y – 1 = xy + 2x\) A1
\(y = \frac{{2x + 1}}{{2 – x}}\) A1
THEN
\({f^{ – 1}}(x) = \frac{{2x + 1}}{{2 – x}}\) A1
Note: Accept \(\frac{5}{{2 – x}} – 2\)
(ii), (iii)
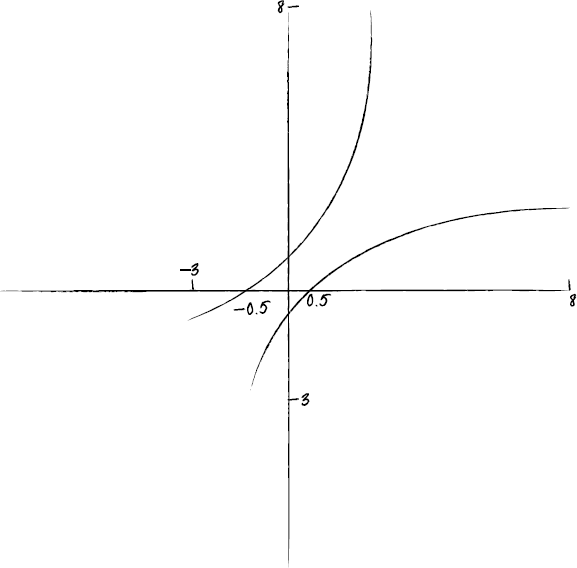A1A1A1A1
[8 marks]
Note: Award A1 for correct shape of \(y = f(x)\).
Award A1 for x intercept \(\frac{1}{2}\) seen. Award A1 for y intercept \( – \frac{1}{2}\) seen.
Award A1 for the graph of \(y = {f^{ – 1}}(x)\) being the reflection of \(y = f(x)\) in the line \(y = x\). Candidates are not required to indicate the full domain, but \(y = f(x)\) should not be shown approaching \(x = – 2\). Candidates, in answering (iii), can FT on their sketch in (ii).
(i)
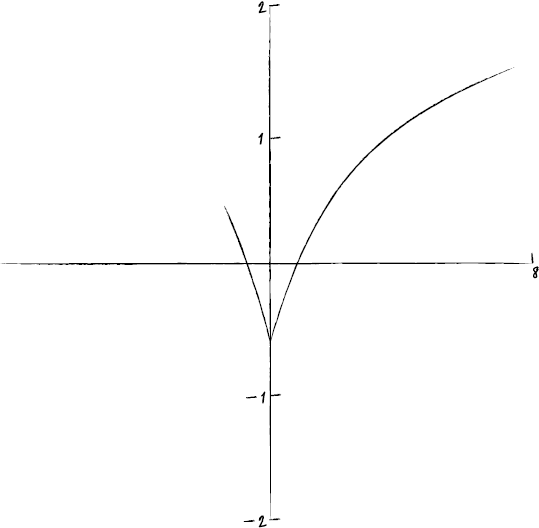A1A1A1
Note: A1 for correct sketch \(x > 0\), A1 for symmetry, A1 for correct domain (from –1 to +8).
Note: Candidates can FT on their sketch in (d)(ii).
(ii) attempt to solve \(f(x) = – \frac{1}{4}\) (M1)
obtain \(x = \frac{2}{9}\) A1
use of symmetry or valid algebraic approach (M1)
obtain \(x = – \frac{2}{9}\) A1
[7 marks]
Question
The function \(f\) is given by \(f(x) = x{{\text{e}}^{ – x}}{\text{ }}(x \geqslant 0)\).
(i) Find an expression for \(f'(x)\).
(ii) Hence determine the coordinates of the point A, where \(f'(x) = 0\).[3]
Find an expression for \(f”(x)\) and hence show the point A is a maximum.[3]
Find the coordinates of B, the point of inflexion.[2]
The graph of the function \(g\) is obtained from the graph of \(f\) by stretching it in the x-direction by a scale factor 2.
(i) Write down an expression for \(g(x)\).
(ii) State the coordinates of the maximum C of \(g\).
(iii) Determine the x-coordinates of D and E, the two points where \(f(x) = g(x)\).[5]
Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the same axes, showing clearly the points A, B, C, D and E.[4]
Find an exact value for the area of the region bounded by the curve \(y = g(x)\), the x-axis and the line \(x = 1\).[3]
Answer/Explanation
Markscheme
(i) \(f'(x) = {{\text{e}}^{ – x}} – x{{\text{e}}^{ – x}}\) M1A1
(ii) \(f'(x) = 0 \Rightarrow x = 1\)
coordinates \(\left( {1,{\text{ }}{{\text{e}}^{ – 1}}} \right)\) A1
[3 marks]
\(f”(x) = – {{\text{e}}^{ – x}} – {{\text{e}}^{ – x}} + x{{\text{e}}^{ – x}}{\text{ }}\left( { = – {{\text{e}}^{ – x}}(2 – x)} \right)\) A1
substituting \(x = 1\) into \(f”(x)\) M1
\(f”(1){\text{ }}\left( { = – {{\text{e}}^{ – 1}}} \right) < 0\) hence maximum R1AG
[3 marks]
\(f”(x) = 0{\text{ (}} \Rightarrow x = 2)\) M1
coordinates \(\left( {2,{\text{ 2}}{{\text{e}}^{ – 2}}} \right)\) A1
[2 marks]
(i) \(g(x) = \frac{x}{2}{{\text{e}}^{ – \frac{x}{2}}}\) A1
(ii) coordinates of maximum \(\left( {2,{\text{ }}{{\text{e}}^{ – 1}}} \right)\) A1
(iii) equating \(f(x) = g(x)\) and attempting to solve \(x{{\text{e}}^{ – x}} = \frac{x}{2}{{\text{e}}^{ – \frac{x}{2}}}\)
\( \Rightarrow x\left( {2{{\text{e}}^{\frac{x}{2}}} – {{\text{e}}^x}} \right) = 0\) (A1)
\( \Rightarrow x = 0\) A1
or \(2{{\text{e}}^{\frac{x}{2}}} = {{\text{e}}^x}\)
\( \Rightarrow {{\text{e}}^{\frac{x}{2}}} = 2\)
\( \Rightarrow x = 2\ln 2\) \((\ln 4)\) A1
Note: Award first (A1) only if factorisation seen or if two correct
solutions are seen.
A4
Note: Award A1 for shape of \(f\), including domain extending beyond \(x = 2\).
Ignore any graph shown for \(x < 0\).
Award A1 for A and B correctly identified.
Award A1 for shape of \(g\), including domain extending beyond \(x = 2\).
Ignore any graph shown for \(x < 0\). Allow follow through from \(f\).
Award A1 for C, D and E correctly identified (D and E are interchangeable).
[4 marks]
\(A = \int_0^1 {\frac{x}{2}{{\text{e}}^{ – \frac{x}{2}}}{\text{d}}x} \) M1
\( = \left[ { – x{{\text{e}}^{ – \frac{x}{2}}}} \right]_0^1 – \int_0^1 { – {{\text{e}}^{ – \frac{x}{2}}}{\text{d}}x} \) A1
Note: Condone absence of limits or incorrect limits.
\( = – {{\text{e}}^{ – \frac{1}{2}}} – \left[ {2{{\text{e}}^{ – \frac{x}{2}}}} \right]_0^1\)
\( = – {{\text{e}}^{ – \frac{1}{2}}} – \left( {2{{\text{e}}^{ – \frac{1}{2}}} – 2} \right) = 2 – 3{{\text{e}}^{ – \frac{1}{2}}}\) A1
[3 marks]
Question
Consider the function \(f(x) = \frac{{\ln x}}{x},{\text{ }}x > 0\).
The sketch below shows the graph of \(y = {\text{ }}f(x)\) and its tangent at a point A.
Show that \(f'(x) = \frac{{1 – \ln x}}{{{x^2}}}\).[2]
Find the coordinates of B, at which the curve reaches its maximum value.[3]
Find the coordinates of C, the point of inflexion on the curve.[5]
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the equation of the tangent to the graph of \(f\) at the point A.[4]
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the area enclosed by the curve \(y = f(x)\), the tangent at A, and the line \(x = {\text{e}}\).[7]
Answer/Explanation
Markscheme
\(f'(x) = \frac{{x \times \frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\) AG
[2 marks]
\(\frac{{1 – \ln x}}{{{x^2}}} = 0\) has solution \(x = {\text{e}}\) M1A1
\(y = \frac{1}{{\text{e}}}\) A1
hence maximum at the point \(\left( {{\text{e, }}\frac{1}{{\text{e}}}} \right)\)
[3 marks]
\(f”(x) = \frac{{{x^2}\left( { – \frac{1}{x}} \right) – 2x(1 – \ln x)}}{{{x^4}}}\) M1A1
\( = \frac{{2\ln x – 3}}{{{x^3}}}\)
Note: The M1A1 should be awarded if the correct working appears in part (b).
point of inflexion where \(f”(x) = 0\) M1
so \(x = {{\text{e}}^{\frac{3}{2}}},{\text{ }}y = \frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}\) A1A1
C has coordinates \(\left( {{{\text{e}}^{\frac{3}{2}}},{\text{ }}\frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}} \right)\)
[5 marks]
\(f(1) = 0\) A1
\(f'(1) = 1\) (A1)
\(y = x + c\) (M1)
through (1, 0)
equation is \(y = x – 1\) A1
[4 marks]
METHOD 1
area \( = \int_1^{\text{e}} {x – 1 – \frac{{\ln x}}{x}{\text{d}}x} \) M1A1A1
Note: Award M1 for integration of difference between line and curve, A1 for correct limits, A1 for correct expressions in either order.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}} ( + c)\) (M1)A1
\(\int {(x – 1){\text{d}}x = \frac{{{x^2}}}{2} – x( + c)} \) A1
\( = \left[ {\frac{1}{2}{x^2} – x – \frac{1}{2}{{(\ln x)}^2}} \right]_1^{\text{e}}\)
\( = \left( {\frac{1}{2}{{\text{e}}^2} – {\text{e}} – \frac{1}{2}} \right) – \left( {\frac{1}{2} – 1} \right)\)
\( = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
METHOD 2
area = area of triangle \( – \int_1^e {\frac{{\ln x}}{x}{\text{d}}x} \) M1A1
Note: A1 is for correct integral with limits and is dependent on the M1.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}( + c)} \) (M1)A1
area of triangle \( = \frac{1}{2}(e – 1)(e – 1)\) M1A1
\(\frac{1}{2}(e – 1)(e – 1) – \left( {\frac{1}{2}} \right) = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
[7 marks]
Question
The graph of the function \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\) is shown below.
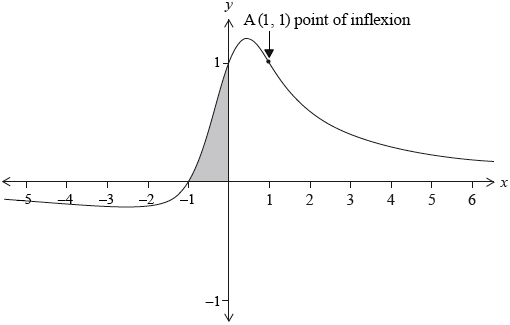
The point (1, 1) is a point of inflexion. There are two other points of inflexion.
Find \(f'(x)\).[2]
Hence find the \(x\)-coordinates of the points where the gradient of the graph of \(f\) is zero.[1]
Find \(f”(x)\) expressing your answer in the form \(\frac{{p(x)}}{{{{({x^2} + 1)}^3}}}\), where \(p(x)\) is a polynomial of degree 3.[3]
Find the \(x\)-coordinates of the other two points of inflexion.[4]
Find the area of the shaded region. Express your answer in the form \(\frac{\pi }{a} – \ln \sqrt b \), where \(a\) and \(b\) are integers.[6]
Answer/Explanation
Markscheme
(a) \(f'(x) = \frac{{\left( {{x^2} + 1} \right) – 2x(x + 1)}}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{ }}\left( { = \frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} \right)\) M1A1
[2 marks]
\(\frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0\)
\(x = – 1 \pm \sqrt 2 \) A1
[1 mark]
\(f”(x) = \frac{{( – 2x – 2){{\left( {{x^2} + 1} \right)}^2} – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^4}}}\) A1A1
Note: Award A1 for \(( – 2x – 2){\left( {{x^2} + 1} \right)^2}\) or equivalent.
Note: Award A1 for \( – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)\) or equivalent.
\( = \frac{{( – 2x – 2)\left( {{x^2} + 1} \right) – 4x\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}\)
\( = \frac{{2{x^3} + 6{x^2} – 6x – 2}}{{{{\left( {{x^2} + 1} \right)}^3}}}\) A1
\(\left( { = \frac{{2\left( {{x^3} + 3{x^2} – 3x – 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}} \right)\)
[3 marks]
recognition that \((x – 1)\) is a factor (R1)
\((x – 1)\left( {{x^2} + bx + c} \right) = \left( {{x^3} + 3{x^2} – 3x – 1} \right)\) M1
\( \Rightarrow {x^2} + 4x + 1 = 0\) A1
\(x = – 2 \pm \sqrt 3 \) A1
Note: Allow long division / synthetic division.
[4 marks]
\(\int_{ – 1}^0 {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x} \) M1
\(\int {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x = \int {\frac{x}{{{x^2} + 1}}{\text{d}}x + \int {\frac{1}{{{x^2} + 1}}{\text{d}}x} } } \) M1
\( = \frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)\) A1A1
\( = \left[ {\frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)} \right]_{ – 1}^0 = \frac{1}{2}\ln 1 + \arctan 0 – \frac{1}{2}\ln 2 – \arctan ( – 1)\) M1
\( = \frac{\pi }{4} – \ln \sqrt 2 \) A1
[6 marks]
Question
A tranquilizer is injected into a muscle from which it enters the bloodstream.
The concentration \(C\) in \({\text{mg}}{{\text{l}}^{ – 1}}\), of tranquilizer in the bloodstream can be modelled by the function \(C(t) = \frac{{2t}}{{3 + {t^2}}},{\text{ }}t \ge 0\) where \(t\) is the number of minutes after the injection.
Find the maximum concentration of tranquilizer in the bloodstream.
Answer/Explanation
Markscheme
use of the quotient rule or the product rule M1
\(C'(t) = \frac{{(3 + {t^2}) \times 2 – 2t \times 2t}}{{{{\left( {3 + {t^2}} \right)}^2}}}\;\;\;\left( { = \frac{{6 – 2{t^2}}}{{{{\left( {3 + {t^2}} \right)}^2}}}} \right)\;\;\;{\text{or}}\;\;\;\frac{2}{{3 + {t^2}}} – \frac{{4{t^2}}}{{{{\left( {3 + {t^2}} \right)}^2}}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator in the quotient rule, and A1 for each correct term in the product rule.
attempting to solve \(C'(t) = 0\;\;\;{\text{for }}t\) (M1)
\(t = \pm \sqrt 3 \;\;\;{\text{(minutes)}}\) A1
\(C\left( {\sqrt 3 } \right) = \frac{{\sqrt 3 }}{3}\;\;\;\left( {{\text{mg}}{{\text{l}}^{ – 1}}} \right)\;\;\;{\text{or equivalent.}}\) A1
[6 marks]
Question
Consider two functions \(f\) and \(g\) and their derivatives \(f’\) and \(g’\). The following table shows the values for the two functions and their derivatives at \(x = 1\), \(2\) and \(3\).
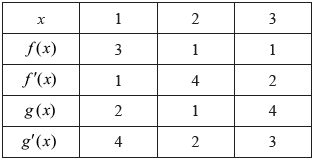
Given that \(p(x) = f(x)g(x)\) and \(h(x) = g \circ f(x)\), find
\(p'(3)\);[2]
\(h'(2)\).[4]
Answer/Explanation
Markscheme
\(p'(3) = f'(3)g(3) + g'(3)f(3)\) (M1)
Note: Award M1 if the derivative is in terms of \(x\) or \(3\).
\( = 2 \times 4 + 3 \times 1\)
\( = 11\) A1
[2 marks]
\(h'(x) = g’\left( {f(x)} \right)f'(x)\) (M1)(A1)
\(h'(2) = g'(1)f'(2)\) A1
\( = 4 \times 4\)
\( = 16\) A1
[4 marks]
Total [6 marks]
Question
Let \(y(x) = x{e^{3x}},{\text{ }}x \in \mathbb{R}\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
Prove by induction that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n – 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\) for \(n \in {\mathbb{Z}^ + }\).[7]
Find the coordinates of any local maximum and minimum points on the graph of \(y(x)\).
Justify whether any such point is a maximum or a minimum.[5]
Find the coordinates of any points of inflexion on the graph of \(y(x)\). Justify whether any such point is a point of inflexion.[5]
Hence sketch the graph of \(y(x)\), indicating clearly the points found in parts (c) and (d) and any intercepts with the axes.[2]
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = ({{\text{e}}^{3x}} + 3x{{\text{e}}^{3x}})\) M1A1
[2 marks]
let \(P(n)\) be the statement \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n – 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\)
prove for \(n = 1\) M1
\(LHS\) of \(P(1)\) is \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) which is \(1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}}\) and \(RHS\) is \({3^0}{{\text{e}}^{3x}} + x{3^1}{{\text{e}}^{3x}}\) R1
as \({\text{LHS}} = {\text{RHS, }}P(1)\) is true
assume \(P(k)\) is true and attempt to prove \(P(k + 1)\) is true M1
assuming \(\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = k{3^{k – 1}}{{\text{e}}^{3x}} + x{3^k}{{\text{e}}^{3x}}\)
\(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}}} \right)\) (M1)
\( = k{3^{k – 1}} \times 3{{\text{e}}^{3x}} + 1 \times {3^k}{{\text{e}}^{3x}} + x{3^k} \times 3{{\text{e}}^{3x}}\) A1
\( = (k + 1){3^k}{{\text{e}}^{3x}} + x{3^{k + 1}}{{\text{e}}^{3x}}\;\;\;\)(as required) A1
Note: Can award the A marks independent of the M marks
since \(P(1)\) is true and \(P(k)\) is true \( \Rightarrow P(k + 1)\) is true
then (by \(PMI\)), \(P(n)\) is true \((\forall n \in {\mathbb{Z}^ + })\) R1
Note: To gain last R1 at least four of the above marks must have been gained.
[7 marks]
\({{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = 0 \Rightarrow 1 + 3x = 0 \Rightarrow x = – \frac{1}{3}\) M1A1
point is \(\left( { – \frac{1}{3},{\text{ }} – \frac{1}{{3{\text{e}}}}} \right)\) A1
EITHER
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\)
when \(x = – \frac{1}{3},{\text{ }}\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} > 0\) therefore the point is a minimum M1A1
OR
nature table shows point is a minimum M1A1
[5 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\) A1
\(2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}} = 0 \Rightarrow 2 + 3x = 0 \Rightarrow x = – \frac{2}{3}\) M1A1
point is \(\left( { – \frac{2}{3},{\text{ }} – \frac{2}{{3{{\text{e}}^2}}}} \right)\) A1
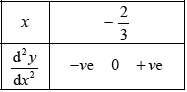
since the curvature does change (concave down to concave up) it is a point of inflection R1
Note: Allow \({3^{{\text{rd}}}}\) derivative is not zero at \( – \frac{2}{3}\)
[5 marks]
(general shape including asymptote and through origin) A1
showing minimum and point of inflection A1
Note: Only indication of position of answers to (c) and (d) required, not coordinates.
[2 marks]
Total [21 marks]
Question
Consider the functions \(f(x) = \tan x,{\text{ }}0 \le \ x < \frac{\pi }{2}\) and \(g(x) = \frac{{x + 1}}{{x – 1}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 1\).
Find an expression for \(g \circ f(x)\), stating its domain.[2]
Hence show that \(g \circ f(x) = \frac{{\sin x + \cos x}}{{\sin x – \cos x}}\).[2]
Let \(y = g \circ f(x)\), find an exact value for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) at the point on the graph of \(y = g \circ f(x)\) where \(x = \frac{\pi }{6}\), expressing your answer in the form \(a + b\sqrt 3 ,{\text{ }}a,{\text{ }}b \in \mathbb{Z}\).[6]
Show that the area bounded by the graph of \(y = g \circ f(x)\), the \(x\)-axis and the lines \(x = 0\) and \(x = \frac{\pi }{6}\) is \(\ln \left( {1 + \sqrt 3 } \right)\).[6]
Answer/Explanation
Markscheme
\(g \circ f(x) = \frac{{\tan x + 1}}{{\tan x – 1}}\) A1
\(x \ne \frac{\pi }{4},{\text{ }}0 \le x < \frac{\pi }{2}\) A1
[2 marks]
\(\frac{{\tan x + 1}}{{\tan x – 1}} = \frac{{\frac{{\sin x}}{{\cos x}} + 1}}{{\frac{{\sin x}}{{\cos x}} – 1}}\) M1A1
\( = \frac{{\sin x + \cos x}}{{\sin x – \cos x}}\) AG
[2 marks]
METHOD 1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(\sin x – \cos x)(\cos x – \sin x) – (\sin x + \cos x)(\cos x + \sin x)}}{{{{(\sin x – \cos x)}^2}}}\) M1(A1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(2\sin x\cos x – {{\cos }^2}x – {{\sin }^2}x) – (2\sin x\cos x + {{\cos }^2}x + {{\sin }^2}x)}}{{{{\cos }^2}x + {{\sin }^2}x – 2\sin x\cos x}}\)
\( = \frac{{ – 2}}{{1 – \sin 2x}}\)
Substitute \(\frac{\pi }{6}\) into any formula for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
\(\frac{{ – 2}}{{1 – \sin \frac{\pi }{3}}}\)
\( = \frac{{ – 2}}{{1 – \frac{{\sqrt 3 }}{2}}}\) A1
\( = \frac{{ – 4}}{{2 – \sqrt 3 }}\)
\( = \frac{{ – 4}}{{2 – \sqrt 3 }}\left( {\frac{{2 + \sqrt 3 }}{{2 + \sqrt 3 }}} \right)\) M1
\( = \frac{{ – 8 – 4\sqrt 3 }}{1} = – 8 – 4\sqrt 3 \) A1
METHOD 2
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(\tan x – 1){{\sec }^2}x – (\tan x + 1){{\sec }^2}x}}{{{{(\tan x – 1)}^2}}}\) M1A1
\( = \frac{{ – 2{{\sec }^2}x}}{{{{(\tan x – 1)}^2}}}\) A1
\( = \frac{{ – 2{{\sec }^2}\frac{\pi }{6}}}{{{{\left( {\tan \frac{\pi }{6} – 1} \right)}^2}}} = \frac{{ – 2\left( {\frac{4}{3}} \right)}}{{{{\left( {\frac{1}{{\sqrt 3 }} – 1} \right)}^2}}} = \frac{{ – 8}}{{{{\left( {1 – \sqrt 3 } \right)}^2}}}\) M1
Note: Award M1 for substitution \(\frac{\pi }{6}\).
\(\frac{{ – 8}}{{{{\left( {1 – \sqrt 3 } \right)}^2}}} = \frac{{ – 8}}{{\left( {4 – 2\sqrt 3 } \right)}}\frac{{\left( {4 + 2\sqrt 3 } \right)}}{{\left( {4 + 2\sqrt 3 } \right)}} = – 8 – 4\sqrt 3 \) M1A1
[6 marks]
Area \(\left| {\int_0^{\frac{\pi }{6}} {\frac{{\sin x + \cos x}}{{\sin x – \cos x}}{\text{d}}x} } \right|\) M1
\( = \left| {\left[ {\ln \left| {\sin x – \cos x} \right|} \right]_0^{\frac{\pi }{6}}} \right|\) A1
Note: Condone absence of limits and absence of modulus signs at this stage.
\( = \left| {\ln \left| {\sin \frac{\pi }{6} – \cos \frac{\pi }{6}} \right| – \ln \left| {\sin 0 – \cos 0} \right|} \right|\) M1
\( = \left| {\ln \left| {\frac{1}{2} – \frac{{\sqrt 3 }}{2}} \right| – 0} \right|\)
\( = \left| {\ln \left( {\frac{{\sqrt 3 – 1}}{2}} \right)} \right|\) A1
\( = – \ln \left( {\frac{{\sqrt 3 – 1}}{2}} \right) = \ln \left( {\frac{2}{{\sqrt 3 – 1}}} \right)\) A1
\( = \ln \left( {\frac{2}{{\sqrt 3 – 1}} \times \frac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}} \right)\) M1
\( = \ln \left( {\sqrt 3 + 1} \right)\) AG
[6 marks]
Total [16 marks]
Question
Consider the function defined by \(f(x) = x\sqrt {1 – {x^2}} \) on the domain \( – 1 \le x \le 1\).
Show that \(f\) is an odd function.[2]
Find \(f'(x)\).[3]
Hence find the \(x\)-coordinates of any local maximum or minimum points.[3]
Find the range of \(f\).[3]
Sketch the graph of \(y = f(x)\) indicating clearly the coordinates of the \(x\)-intercepts and any local maximum or minimum points.[3]
Find the area of the region enclosed by the graph of \(y = f(x)\) and the \(x\)-axis for \(x \ge 0\).[4]
Show that \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \).[2]
Answer/Explanation
Markscheme
\(f( – x) = ( – x)\sqrt {1 – {{( – x)}^2}} \) M1
\( = – x\sqrt {1 – {x^2}} \)
\( = – f(x)\) R1
hence \(f\) is odd AG
[2 marks]
\(f'(x) = x \bullet \frac{1}{2}{(1 – {x^2})^{ – \frac{1}{2}}} \bullet – 2x + {(1 – {x^2})^{\frac{1}{2}}}\) M1A1A1
[3 marks]
\(f'(x) = \sqrt {1 – {x^2}} – \frac{{{x^2}}}{{\sqrt {1 – {x^2}} }}\;\;\;\left( { = \frac{{1 – 2{x^2}}}{{\sqrt {1 – {x^2}} }}} \right)\) A1
Note: This may be seen in part (b).
Note: Do not allow FT from part (b).
\(f'(x) = 0 \Rightarrow 1 – 2{x^2} = 0\) M1
\(x = \pm \frac{1}{{\sqrt 2 }}\) A1
[3 marks]
\(y\)-coordinates of the Max Min Points are \(y = \pm \frac{1}{2}\) M1A1
so range of \(f(x)\) is \(\left[ { – \frac{1}{2},{\text{ }}\frac{1}{2}} \right]\) A1
Note: Allow FT from (c) if values of \(x\), within the domain, are used.
[3 marks]
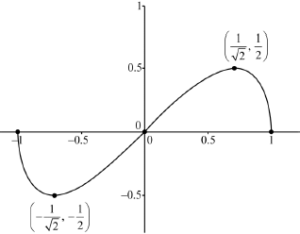
Shape: The graph of an odd function, on the given domain, s-shaped,
where the max(min) is the right(left) of \(0.5{\text{ }}( – 0.5)\) A1
\(x\)-intercepts A1
turning points A1
[3 marks]
\({\text{area}} = \int_0^1 {x\sqrt {1 – {x^2}} {\text{d}}x} \) (M1)
attempt at “backwards chain rule” or substitution M1
\( = – \frac{1}{2}\int_0^1 {( – 2x)\sqrt {1 – {x^2}} {\text{d}}x} \)
Note: Condone absence of limits for first two marks.
\( = \left[ {\frac{2}{3}{{(1 – {x^2})}^{\frac{3}{2}}} \bullet – \frac{1}{2}} \right]_0^1\) A1
\( = \left[ { – \frac{1}{3}{{(1 – {x^2})}^{\frac{3}{2}}}} \right]_0^1\)
\( = 0 – \left( { – \frac{1}{3}} \right) = \frac{1}{3}\) A1
[4 marks]
\(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > 0} \) R1
\(\left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right| = 0\) R1
so \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \) AG
[2 marks]
Total [20 marks]
Question
A curve is given by the equation \(y = \sin (\pi \cos x)\).
Find the coordinates of all the points on the curve for which \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0,{\text{ }}0 \leqslant x \leqslant \pi \).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \cos (\pi \cos x) \times \pi \sin x\) M1A1
Note: Award follow through marks below if their answer is a multiple of the correct answer.
considering either \(\sin x = 0\) or \(\cos (\pi \cos x) = 0\) (M1)
\(x = 0,{\text{ }}\pi \) A1
\(\pi \cos x = \frac{\pi }{2},{\text{ }} – \frac{\pi }{2}{\text{ }}\left( { \Rightarrow \cos x = \frac{1}{2}, – \frac{1}{2}} \right)\) M1
Note: Condone absence of \( – \frac{\pi }{2}\).
\( \Rightarrow x = \frac{\pi }{3},{\text{ }}\frac{{2\pi }}{3}\)
\((0,{\text{ }}0),{\text{ }}\left( {\frac{\pi }{3},{\text{ 1}}} \right),{\text{ (}}\pi {\text{, 0)}}\) A1
\(\left( {\frac{{2\pi }}{3},{\text{ }} – 1} \right)\) A1
[7 marks]
Question
The following graph shows the relation \(x = 3\cos 2y + 4,{\text{ }}0 \leqslant y \leqslant \pi \).
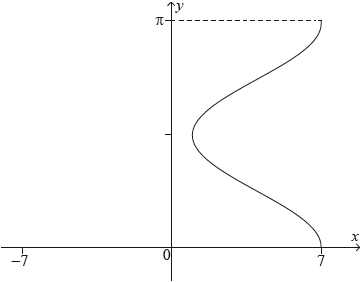
The curve is rotated 360° about the \(y\)-axis to form a volume of revolution.
A container with this shape is made with a solid base of diameter 14 cm . The container is filled with water at a rate of \({\text{2 c}}{{\text{m}}^{\text{3}}}\,{\text{mi}}{{\text{n}}^{ – 1}}\). At time \(t\) minutes, the water depth is \(h{\text{ cm, }}0 \leqslant h \leqslant \pi \) and the volume of water in the container is \(V{\text{ c}}{{\text{m}}^{\text{3}}}\).
Calculate the value of the volume generated.[8]
(i) Given that \(\frac{{{\text{d}}V}}{{{\text{d}}h}} = \pi {(3\cos 2h + 4)^2}\), find an expression for \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\).
(ii) Find the value of \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) when \(h = \frac{\pi }{4}\).[4]
(i) Find \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(ii) Find the values of \(h\) for which \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = 0\).
(iii) By making specific reference to the shape of the container, interpret \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) at the values of \(h\) found in part (c)(ii).[7]
Answer/Explanation
Markscheme
use of \(\pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
Note: Condone any or missing limits.
\(V = \pi \int_0^\pi {{{(3\cos 2y + 4)}^2}{\text{d}}y} \) (A1)
\( = \pi \int_0^\pi {(9{{\cos }^2}2y + 24\cos 2y + 16){\text{d}}y} \) A1
\(9{\cos ^2}2y = \frac{9}{2}(1 + \cos 4y)\) (M1)
\( = \pi \left[ {\frac{{9y}}{2} + \frac{9}{8}\sin 4y + 12\sin 2y + 16y} \right]_0^\pi \) M1A1
\( = \pi \left( {\frac{{9\pi }}{2} + 16\pi } \right)\) (A1)
\( = \frac{{41{\pi ^2}}}{2}{\text{ (c}}{{\text{m}}^3})\) A1
Note: If the coefficient “\(\pi \)” is absent, or eg, “\(2\pi \)” is used, only M marks are available.
[8 marks]
(i) attempting to use \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}V}}{{{\text{d}}t}} \times \frac{{{\text{d}}h}}{{{\text{d}}V}}\) with \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 2\) M1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}}\) A1
(ii) substituting \(h = \frac{\pi }{4}\) into \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{8\pi }}{\text{ (cm}}\,{\text{mi}}{{\text{n}}^{ – 1}})\) A1
Note: Do not allow FT marks for (b)(ii).
[4 marks]
(i) \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right) = \frac{{{\text{d}}h}}{{{\text{d}}t}} \times \frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\) (M1)
\( = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}} \times \frac{{24\sin 2h}}{{\pi {{(3\cos 2h + 4)}^3}}}\) M1A1
Note: Award M1 for attempting to find \(\frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\).
\( = \frac{{48\sin 2h}}{{{\pi ^2}{{(3\cos 2h + 4)}^5}}}\) A1
(ii) \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) A1
Note: Award A1 for \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) from an incorrect \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(iii) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a minimum at \(h = 0,{\text{ }}\pi \) and the container is widest at these values R1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a maximum at \(h = \frac{\pi }{2}\) and the container is narrowest at this value R1
[7 marks]
Question
Let \(y = {{\text{e}}^x}\sin x\).
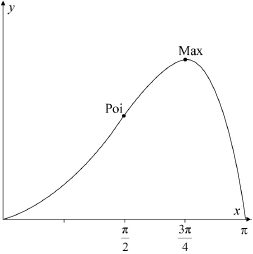
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).[2]
Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).[2]
Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).[2]
Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.[3]
Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).[6]
Find the value of the curvature of the graph of \(f\) at the local maximum point.[3]
Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.[2]
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Question
Let \(y = {\text{si}}{{\text{n}}^2}\theta ,\,\,0 \leqslant \theta \leqslant \pi \).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}\theta }}\)[2]
Hence find the values of θ for which \(\frac{{{\text{d}}y}}{{{\text{d}}\theta }} = 2y\).[5]
Answer/Explanation
Markscheme
attempt at chain rule or product rule (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}\theta }} = 2\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta \) A1
[2 marks]
\(2\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta = 2{\text{si}}{{\text{n}}^2}\theta \)
sin θ = 0 (A1)
θ = 0, \(\pi \) A1
obtaining cos θ = sin θ (M1)
tan θ = 1 (M1)
\(\theta = \frac{\pi }{4}\) A1
[5 marks]
Question
Let \(y = {\text{arccos}}\left( {\frac{x}{2}} \right)\)
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
Find \(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} \).[7]
Answer/Explanation
Markscheme
\(y = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{{2\sqrt {1 – {{\left( {\frac{x}{2}} \right)}^2}} }}\left( { = – \frac{1}{{\sqrt {4 – {x^2}} }}} \right)\) M1A1
Note: M1 is for use of the chain rule.
[2 marks]
attempt at integration by parts M1
\(u = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}u}}{{{\text{d}}x}} = – \frac{1}{{\sqrt {4 – {x^2}} }}\)
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 1 \Rightarrow v = x\) (A1)
\(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} = \left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \int_0^1 {\frac{1}{{\sqrt {4 – {x^2}} }}} dx\) A1
using integration by substitution or inspection (M1)
\(\left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \left[ { – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}} \right]_0^1\) A1
Note: Award A1 for \({ – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}}\) or equivalent.
Note: Condone lack of limits to this point.
attempt to substitute limits into their integral M1
\( = \frac{\pi }{3} – \sqrt 3 + 2\) A1
[7 marks]
Question
Consider the functions \(f,\,\,g,\) defined for \(x \in \mathbb{R}\), given by \(f\left( x \right) = {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) and \(g\left( x \right) = {{\text{e}}^{ – x}}\,{\text{cos}}\,x\).
Find \(f’\left( x \right)\).[2]
Find \(g’\left( x \right)\).[1]
Hence, or otherwise, find \(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} \).[4]
Answer/Explanation
Markscheme
attempt at product rule M1
\(f’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + {{\text{e}}^{ – x}}\,{\text{cos}}\,x\) A1
[2 marks]
\(g’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
[1 mark]
METHOD 1
Attempt to add \(f’\left( x \right)\) and \(g’\left( x \right)\) (M1)
\(f’\left( x \right) + g’\left( x \right) = – 2{{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
\(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} = \left[ { – \frac{{{{\text{e}}^{ – x}}}}{2}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)} \right]_0^\pi \) (or equivalent) A1
Note: Condone absence of limits.
\( = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)\) A1
METHOD 2
\(I = \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\( = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) OR \( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) M1A1
\( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\(I = \frac{1}{2}{{\text{e}}^{ – x}}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)\) A1
\(\int_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)} \) A1
[4 marks]