Question
(a) Let \(a > 0\) . Draw the graph of \(y = \left| {x – \frac{a}{2}} \right|\) for \( – a \leqslant x \leqslant a\) on the grid below.

(b) Find k such that \(\int_{ – a}^0 {\left| {x – \frac{a}{2}} \right|{\text{d}}x = k\int_0^a {\left| {x – \frac{a}{2}} \right|{\text{d}}x} } \) .
Answer/Explanation
Markscheme
(a)
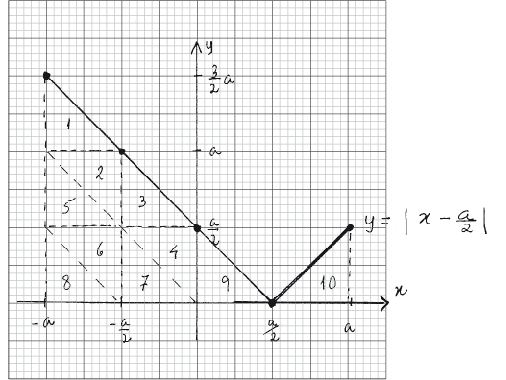 A1A1
A1A1
Note: Award A1 for the correct x-intercept,
A1 for completely correct graph.
(b) METHOD 1
the area under the graph of \(y = \left| {x – \frac{a}{2}} \right|\) for \( – a \leqslant x \leqslant a\) , can be divided into ten congruent triangles; M1A1
the area of eight of these triangles is given by \(\int_{ – a}^0 {\left| {x – \frac{a}{2}} \right|{\text{d}}x} \) and the areas of the other two by \(\int_0^a {\left| {x – \frac{a}{2}} \right|{\text{d}}x} \) M1A1
so, \(\int_{ – a}^0 {\left| {x – \frac{a}{2}} \right|{\text{d}}x} = 4\int_0^a {\left| {x – \frac{a}{2}} \right|{\text{d}}x} \Rightarrow k = 4\) A1 N0
METHOD 2
use area of trapezium to calculate M1
\(\int_{ – a}^0 {\left| {x – \frac{a}{2}} \right|{\text{d}}x} = a \times \frac{1}{2}\left( {\frac{{3a}}{2} + \frac{a}{2}} \right) = {a^2}\) A1
and area of two triangles to obtain M1
\(\int_0^a {\left| {x – \frac{a}{2}} \right|{\text{d}}x} = 2 \times \frac{1}{2}{\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}\) A1
so, k = 4 A1 N0
METHOD 3
use integration to find the area under the curve
\(\int_{ – a}^0 {\left| {x – \frac{a}{2}} \right|{\text{d}}x} = \int_{ – a}^0 { – x + \frac{a}{2}{\text{d}}x} \) M1
\( = \left[ { – \frac{{{x^2}}}{2} + \frac{a}{2}x} \right]_{ – a}^0 = \frac{{{a^2}}}{2} + \frac{{{a^2}}}{2} = {a^2}\) A1
and
\(\int_0^a {\left| {x – \frac{a}{2}} \right|{\text{d}}x} = \int_0^{\frac{a}{2}} { – x + \frac{a}{2}{\text{d}}x + \int_{\frac{a}{2}}^a {x – \frac{a}{2}{\text{d}}x} } \) M1
\( = \left[ { – \frac{{{x^2}}}{2} + \frac{a}{2}x} \right]_0^{\frac{a}{2}} + \left[ {\frac{{{x^2}}}{2} – \frac{a}{2}x} \right]_{\frac{a}{2}}^a = \frac{{{a^2}}}{8} + \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} – \frac{{{a^2}}}{2} – \frac{{{a^2}}}{8} + \frac{{{a^2}}}{4} = \frac{{{a^2}}}{4}\) A1
so, k = 4 A1 N0
[7 marks]
Examiners report
Most candidates attempted this question but very often produced sketches lacking labels on axes and intercepts or ignored the domain of the function. For part (b) many candidates attempted to use integration to find the areas but seldom considered the absolute value. A small number of candidates used geometrical methods to determine the areas, showing good understanding of the problem.
Question
(a) Show that \(\frac{3}{{x + 1}} + \frac{2}{{x + 3}} = \frac{{5x + 11}}{{{x^2} + 4x + 3}}\).
(b) Hence find the value of k such that \(\int_0^2 {\frac{{5x + 11}}{{{x^2} + 4x + 3}}{\text{d}}x = \ln k} \) .
Answer/Explanation
Markscheme
(a) \(\frac{3}{{x + 1}} + \frac{2}{{x + 3}} = \frac{{3(x + 3) + 2(x + 1)}}{{(x + 1)(x + 3)}}\) M1
\( = \frac{{3x + 9 + 2x + 2}}{{{x^2} + 4x + 3}}\) A1
\( = \frac{{5x + 11}}{{{x^2} + 4x + 3}}\) AG
(b) \(\int_0^2 {\frac{{5x + 11}}{{{x^2} + 4x + 3}}{\text{d}}x} = \int_0^2 {\left( {\frac{3}{{x + 1}} + \frac{2}{{x + 3}}} \right){\text{d}}x} \) M1
\( = \left[ {3\ln (x + 1) + 2\ln (x + 3)} \right]_0^2\) A1
\( = 3\ln 3 + 2\ln 5 – 3\ln 1 – 2\ln 3\,\,\,\,\,( = 3\ln 3 + 2\ln 5 – 2\ln 3)\) A1
\( = \ln 3 + 2\ln 5\)
\( = \ln 75\,\,\,\,\,(k = 75)\) A1
[6 marks]
Examiners report
Many students did not ‘Show’ enough in a) in order to be convincing. The need for the steps of the simplification to be shown was not clear. Too many did not link a) to b) and seemed to not be aware of the Command Term ‘hence’ and its implication for marking ( no marks will be awarded to alternative methods). The simplifications of the log expressions were done poorly by many and the fact that \({3^3} = 9\) was noted by too many. There were very few elegant solutions to this question.
Question
Find all values of x for \(0.1 \leqslant x \leqslant 1\) such that \(\sin (\pi {x^{ – 1}}) = 0\).
Find \(\int_{\frac{1}{{n + 1}}}^{\frac{1}{n}} {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}}){\text{d}}x} \), showing that it takes different integer values when n is even and when n is odd.
Evaluate \(\int_{0.1}^1 {\left| {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}})} \right|{\text{d}}x} \).
Answer/Explanation
Markscheme
\(\sin (\pi {x^{ – 1}}) = 0{\text{ }}\frac{\pi }{x} = \pi ,{\text{ }}2\pi ( \ldots )\) (A1)
\(x = 1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\frac{1}{7},\frac{1}{8},\frac{1}{9},\frac{1}{{10}}\) A1
[2 marks]
\(\left[ {\cos (\pi {x^{ – 1}})} \right]_{\frac{1}{{n + 1}}}^{\frac{1}{n}}\) M1
\( = \cos (\pi n) – \cos \left( {\pi (n + 1)} \right)\) A1
= 2 when n is even and = –2 when n is odd A1
[3 marks]
\(\int_{0.1}^1 {\left| {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}})} \right|{\text{d}}x} = 2 + 2 + \ldots + 2 = 18\) (M1)A1
[2 marks]
Examiners report
There were a pleasing number of candidates who answered part (a) correctly. Fewer were successful with part (b). It was expected by this stage of the paper that candidates would be able to just write down the value of the integral rather than use substitution to evaluate it.
There were a pleasing number of candidates who answered part (a) correctly. Fewer were successful with part (b). It was expected by this stage of the paper that candidates would be able to just write down the value of the integral rather than use substitution to evaluate it.
There were disappointingly few correct answers to part (c) with candidates not realising that it was necessary to combine the previous two parts in order to write down the answer.
Question
Find all values of x for \(0.1 \leqslant x \leqslant 1\) such that \(\sin (\pi {x^{ – 1}}) = 0\).
Find \(\int_{\frac{1}{{n + 1}}}^{\frac{1}{n}} {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}}){\text{d}}x} \), showing that it takes different integer values when n is even and when n is odd.
Evaluate \(\int_{0.1}^1 {\left| {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}})} \right|{\text{d}}x} \).
Answer/Explanation
Markscheme
\(\sin (\pi {x^{ – 1}}) = 0{\text{ }}\frac{\pi }{x} = \pi ,{\text{ }}2\pi ( \ldots )\) (A1)
\(x = 1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\frac{1}{7},\frac{1}{8},\frac{1}{9},\frac{1}{{10}}\) A1
[2 marks]
\(\left[ {\cos (\pi {x^{ – 1}})} \right]_{\frac{1}{{n + 1}}}^{\frac{1}{n}}\) M1
\( = \cos (\pi n) – \cos \left( {\pi (n + 1)} \right)\) A1
= 2 when n is even and = –2 when n is odd A1
[3 marks]
\(\int_{0.1}^1 {\left| {\pi {x^{ – 2}}\sin (\pi {x^{ – 1}})} \right|{\text{d}}x} = 2 + 2 + \ldots + 2 = 18\) (M1)A1
[2 marks]
Examiners report
There were a pleasing number of candidates who answered part (a) correctly. Fewer were successful with part (b). It was expected by this stage of the paper that candidates would be able to just write down the value of the integral rather than use substitution to evaluate it.
There were a pleasing number of candidates who answered part (a) correctly. Fewer were successful with part (b). It was expected by this stage of the paper that candidates would be able to just write down the value of the integral rather than use substitution to evaluate it.
There were disappointingly few correct answers to part (c) with candidates not realising that it was necessary to combine the previous two parts in order to write down the answer.
Question
Find the exact value of \(\int_1^2 {\left( {{{(x – 2)}^2} + \frac{1}{x} + \sin \pi x} \right){\text{dx}}} \).
Answer/Explanation
Markscheme
\(\left[ {\frac{1}{3}{{(x – 2)}^3} + \ln x – \frac{1}{\pi }\cos \pi x} \right]_{(1)}^{(2)}\) A1A1A1
Note: Accept \(\frac{1}{3}{x^3} – 2{x^2} + 4x\) in place of \(\frac{1}{3}{(x – 2)^3}\).
\( = \left( {0 + \ln 2 – \frac{1}{\pi }\cos 2\pi } \right) – \left( { – \frac{1}{3} + \ln 1 – \frac{1}{\pi }\cos \pi } \right)\) (M1)
\( = \frac{1}{3} + \ln 2 – \frac{2}{\pi }\) A1A1
Note: Award A1 for any two terms correct, A1 for the third correct.
[6 marks]
Examiners report
Generally well done, although quite a number of candidates were either unable to integrate the sine term or incorrectly evaluated the resulting cosine at the limits.
Question
Consider the complex number \(z = \cos \theta + {\text{i}}\sin \theta \).
The region S is bounded by the curve \(y = \sin x{\cos ^2}x\) and the x-axis between \(x = 0\) and \(x = \frac{\pi }{2}\).
Use De Moivre’s theorem to show that \({z^n} + {z^{ – n}} = 2\cos n\theta ,{\text{ }}n \in {\mathbb{Z}^ + }\).
Expand \({\left( {z + {z^{ – 1}}} \right)^4}\).
Hence show that \({\cos ^4}\theta = p\cos 4\theta + q\cos 2\theta + r\), where \(p,{\text{ }}q\) and \(r\) are constants to be determined.
Show that \({\cos ^6}\theta = \frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}\).
Hence find the value of \(\int_0^{\frac{\pi }{2}} {{{\cos }^6}\theta {\text{d}}\theta } \).
S is rotated through \(2\pi \) radians about the x-axis. Find the value of the volume generated.
(i) Write down an expression for the constant term in the expansion of \({\left( {z + {z^{ – 1}}} \right)^{2k}}\), \(k \in {\mathbb{Z}^ + }\).
(ii) Hence determine an expression for \(\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta } \) in terms of k.
Answer/Explanation
Markscheme
\({z^n} + {z^{ – n}} = \cos n\theta + i\sin n\theta + \cos ( – n\theta ) + i\sin ( – n\theta )\) M1
\( = \cos n\theta + \cos n\theta + i\sin n\theta – i\sin n\theta \) A1
\( = 2\cos n\theta \) AG
[2 marks]
(b) \({\left( {z + {z^{ – 1}}} \right)^4} = {z^4} + 4{z^3}\left( {\frac{1}{z}} \right) + 6{z^2}\left( {\frac{1}{{{z^2}}}} \right) + 4z\left( {\frac{1}{{{z^3}}}} \right) + \frac{1}{{{z^4}}}\) A1
Note: Accept \({\left( {z + {z^{ – 1}}} \right)^4} = 16{\cos ^4}\theta \).
[1 mark]
METHOD 1
\({\left( {z + {z^{ – 1}}} \right)^4} = \left( {{z^4} + \frac{1}{{{z^4}}}} \right) + 4\left( {{z^2} + \frac{1}{{{z^2}}}} \right) + 6\) M1
\({(2\cos \theta )^4} = 2\cos 4\theta + 8\cos 2\theta + 6\) A1A1
Note: Award A1 for RHS, A1 for LHS, independent of the M1.
\({\cos ^4}\theta = \frac{1}{8}\cos 4\theta + \frac{1}{2}\cos 2\theta + \frac{3}{8}\) A1
\(\left( {{\text{or }}p = \frac{1}{8},{\text{ }}q = \frac{1}{2},{\text{ }}r = \frac{3}{8}} \right)\)
METHOD 2
\({\cos ^4}\theta = {\left( {\frac{{\cos 2\theta + 1}}{2}} \right)^2}\) M1
\( = \frac{1}{4}({\cos ^2}2\theta + 2\cos 2\theta + 1)\) A1
\( = \frac{1}{4}\left( {\frac{{\cos 4\theta + 1}}{2} + 2\cos 2\theta + 1} \right)\) A1
\({\cos ^4}\theta = \frac{1}{8}\cos 4\theta + \frac{1}{2}\cos 2\theta + \frac{3}{8}\) A1
\(\left( {{\text{or }}p = \frac{1}{8},{\text{ }}q = \frac{1}{2},{\text{ }}r = \frac{3}{8}} \right)\)
[4 marks]
\({\left( {z + {z^{ – 1}}} \right)^6} = {z^6} + 6{z^5}\left( {\frac{1}{z}} \right) + 15{z^4}\left( {\frac{1}{{{z^2}}}} \right) + 20{z^3}\left( {\frac{1}{{{z^3}}}} \right) + 15{z^2}\left( {\frac{1}{{{z^4}}}} \right) + 6z\left( {\frac{1}{{{z^5}}}} \right) + \frac{1}{{{z^6}}}\) M1
\({\left( {z + {z^{ – 1}}} \right)^6} = \left( {{z^6} + \frac{1}{{{z^6}}}} \right) + 6\left( {{z^4} + \frac{1}{{{z^4}}}} \right) + 15\left( {{z^2} + \frac{1}{{{z^2}}}} \right) + 20\)
\({(2\cos \theta )^6} = 2\cos 6\theta + 12\cos 4\theta + 30\cos 2\theta + 20\) A1A1
Note: Award A1 for RHS, A1 for LHS, independent of the M1.
\({\cos ^6}\theta = \frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}\) AG
Note: Accept a purely trigonometric solution as for (c).
[3 marks]
\(\int_0^{\frac{\pi }{2}} {{{\cos }^6}\theta {\text{d}}\theta = \int_0^{\frac{\pi }{2}} {\left( {\frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}} \right){\text{d}}\theta } } \)
\( = \left[ {\frac{1}{{192}}\sin 6\theta + \frac{3}{{64}}\sin 4\theta + \frac{{15}}{{64}}\sin 2\theta + \frac{5}{{16}}\theta } \right]_0^{\frac{\pi }{2}}\) M1A1
\( = \frac{{5\pi }}{{32}}\) A1
[3 marks]
\({\text{V}} = \pi \int_0^{\frac{\pi }{2}} {{{\sin }^2}x{{\cos }^4}x{\text{d}}x} \) M1
\( = \pi \int_0^{\frac{\pi }{2}} {{{\cos }^4}x{\text{d}}x – \pi \int_0^{\frac{\pi }{2}} {{{\cos }^6}x{\text{d}}x} } \) M1
\(\int_0^{\frac{\pi }{2}} {{{\cos }^4}x{\text{d}}x} = \frac{{3\pi }}{{16}}\) A1
\({\text{V}} = \frac{{3{\pi ^2}}}{{16}} – \frac{{5{\pi ^2}}}{{32}} = \frac{{{\pi ^2}}}{{32}}\) A1
Note: Follow through from an incorrect r in (c) provided the final answer is positive.
(i) constant term = \(\left( \begin{array}{c}2k\\k\end{array} \right)\) \( = \frac{{(2k)!}}{{k!k!}} = \frac{{(2k)!}}{{{{(k!)}^2}}}{\text{ (accept }}C_k^{2k})\) A1
(ii) \({2^{2k}}\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta = \frac{{(2k)!\pi }}{{{{(k!)}^2}}}\frac{\pi }{2}} \) A1
\(\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta = \frac{{(2k)!\pi }}{{{2^{2k + 1}}{{(k!)}^2}}}} \) \(\left( {{\rm{or}}\frac{{\left( \begin{array}{c}2k\\k\end{array} \right)\pi }}{{{2^{2k + 1}}}}} \right)\) A1
[3 marks]
Examiners report
Part a) has appeared several times before, though with it again being a ‘show that’ question, some candidates still need to be more aware of the need to show every step in their working, including the result that \(\sin ( – n\theta ) = – \sin (n\theta )\).
Part b) was usually answered correctly.
Part c) was again often answered correctly, though some candidates often less successfully utilised a trig-only approach rather than taking note of part b).
Part d) was a good source of marks for those who kept with the spirit of using complex numbers for this type of question. Some limited attempts at trig-only solutions were seen, and correct solutions using this approach were extremely rare.
Part e) was well answered, though numerical slips were often common. A small number integrated \(\sin n\theta \) as \(n\cos n\theta \).
A large number of candidates did not realise the help that part e) inevitably provided for part f). Some correctly expressed the volume as \(\pi \int {{{\cos }^4}x{\text{d}}x – \pi \int {{{\cos }^6}x{\text{d}}x} } \) and thus gained the first 2 marks but were able to progress no further. Only a small number of able candidates were able to obtain the correct answer of \(\frac{{{\pi ^2}}}{{32}}\).
[N/A]
Part g) proved to be a challenge for the vast majority, though it was pleasing to see some of the highest scoring candidates gain all 3 marks.
Question
Consider the complex number \(z = \cos \theta + {\text{i}}\sin \theta \).
The region S is bounded by the curve \(y = \sin x{\cos ^2}x\) and the x-axis between \(x = 0\) and \(x = \frac{\pi }{2}\).
Use De Moivre’s theorem to show that \({z^n} + {z^{ – n}} = 2\cos n\theta ,{\text{ }}n \in {\mathbb{Z}^ + }\).
Expand \({\left( {z + {z^{ – 1}}} \right)^4}\).
Hence show that \({\cos ^4}\theta = p\cos 4\theta + q\cos 2\theta + r\), where \(p,{\text{ }}q\) and \(r\) are constants to be determined.
Show that \({\cos ^6}\theta = \frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}\).
Hence find the value of \(\int_0^{\frac{\pi }{2}} {{{\cos }^6}\theta {\text{d}}\theta } \).
S is rotated through \(2\pi \) radians about the x-axis. Find the value of the volume generated.
(i) Write down an expression for the constant term in the expansion of \({\left( {z + {z^{ – 1}}} \right)^{2k}}\), \(k \in {\mathbb{Z}^ + }\).
(ii) Hence determine an expression for \(\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta } \) in terms of k.
Answer/Explanation
Markscheme
\({z^n} + {z^{ – n}} = \cos n\theta + i\sin n\theta + \cos ( – n\theta ) + i\sin ( – n\theta )\) M1
\( = \cos n\theta + \cos n\theta + i\sin n\theta – i\sin n\theta \) A1
\( = 2\cos n\theta \) AG
[2 marks]
(b) \({\left( {z + {z^{ – 1}}} \right)^4} = {z^4} + 4{z^3}\left( {\frac{1}{z}} \right) + 6{z^2}\left( {\frac{1}{{{z^2}}}} \right) + 4z\left( {\frac{1}{{{z^3}}}} \right) + \frac{1}{{{z^4}}}\) A1
Note: Accept \({\left( {z + {z^{ – 1}}} \right)^4} = 16{\cos ^4}\theta \).
[1 mark]
METHOD 1
\({\left( {z + {z^{ – 1}}} \right)^4} = \left( {{z^4} + \frac{1}{{{z^4}}}} \right) + 4\left( {{z^2} + \frac{1}{{{z^2}}}} \right) + 6\) M1
\({(2\cos \theta )^4} = 2\cos 4\theta + 8\cos 2\theta + 6\) A1A1
Note: Award A1 for RHS, A1 for LHS, independent of the M1.
\({\cos ^4}\theta = \frac{1}{8}\cos 4\theta + \frac{1}{2}\cos 2\theta + \frac{3}{8}\) A1
\(\left( {{\text{or }}p = \frac{1}{8},{\text{ }}q = \frac{1}{2},{\text{ }}r = \frac{3}{8}} \right)\)
METHOD 2
\({\cos ^4}\theta = {\left( {\frac{{\cos 2\theta + 1}}{2}} \right)^2}\) M1
\( = \frac{1}{4}({\cos ^2}2\theta + 2\cos 2\theta + 1)\) A1
\( = \frac{1}{4}\left( {\frac{{\cos 4\theta + 1}}{2} + 2\cos 2\theta + 1} \right)\) A1
\({\cos ^4}\theta = \frac{1}{8}\cos 4\theta + \frac{1}{2}\cos 2\theta + \frac{3}{8}\) A1
\(\left( {{\text{or }}p = \frac{1}{8},{\text{ }}q = \frac{1}{2},{\text{ }}r = \frac{3}{8}} \right)\)
[4 marks]
\({\left( {z + {z^{ – 1}}} \right)^6} = {z^6} + 6{z^5}\left( {\frac{1}{z}} \right) + 15{z^4}\left( {\frac{1}{{{z^2}}}} \right) + 20{z^3}\left( {\frac{1}{{{z^3}}}} \right) + 15{z^2}\left( {\frac{1}{{{z^4}}}} \right) + 6z\left( {\frac{1}{{{z^5}}}} \right) + \frac{1}{{{z^6}}}\) M1
\({\left( {z + {z^{ – 1}}} \right)^6} = \left( {{z^6} + \frac{1}{{{z^6}}}} \right) + 6\left( {{z^4} + \frac{1}{{{z^4}}}} \right) + 15\left( {{z^2} + \frac{1}{{{z^2}}}} \right) + 20\)
\({(2\cos \theta )^6} = 2\cos 6\theta + 12\cos 4\theta + 30\cos 2\theta + 20\) A1A1
Note: Award A1 for RHS, A1 for LHS, independent of the M1.
\({\cos ^6}\theta = \frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}\) AG
Note: Accept a purely trigonometric solution as for (c).
[3 marks]
\(\int_0^{\frac{\pi }{2}} {{{\cos }^6}\theta {\text{d}}\theta = \int_0^{\frac{\pi }{2}} {\left( {\frac{1}{{32}}\cos 6\theta + \frac{3}{{16}}\cos 4\theta + \frac{{15}}{{32}}\cos 2\theta + \frac{5}{{16}}} \right){\text{d}}\theta } } \)
\( = \left[ {\frac{1}{{192}}\sin 6\theta + \frac{3}{{64}}\sin 4\theta + \frac{{15}}{{64}}\sin 2\theta + \frac{5}{{16}}\theta } \right]_0^{\frac{\pi }{2}}\) M1A1
\( = \frac{{5\pi }}{{32}}\) A1
[3 marks]
\({\text{V}} = \pi \int_0^{\frac{\pi }{2}} {{{\sin }^2}x{{\cos }^4}x{\text{d}}x} \) M1
\( = \pi \int_0^{\frac{\pi }{2}} {{{\cos }^4}x{\text{d}}x – \pi \int_0^{\frac{\pi }{2}} {{{\cos }^6}x{\text{d}}x} } \) M1
\(\int_0^{\frac{\pi }{2}} {{{\cos }^4}x{\text{d}}x} = \frac{{3\pi }}{{16}}\) A1
\({\text{V}} = \frac{{3{\pi ^2}}}{{16}} – \frac{{5{\pi ^2}}}{{32}} = \frac{{{\pi ^2}}}{{32}}\) A1
Note: Follow through from an incorrect r in (c) provided the final answer is positive.
(i) constant term = \(\left( \begin{array}{c}2k\\k\end{array} \right)\) \( = \frac{{(2k)!}}{{k!k!}} = \frac{{(2k)!}}{{{{(k!)}^2}}}{\text{ (accept }}C_k^{2k})\) A1
(ii) \({2^{2k}}\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta = \frac{{(2k)!\pi }}{{{{(k!)}^2}}}\frac{\pi }{2}} \) A1
\(\int_0^{\frac{\pi }{2}} {{{\cos }^{2k}}\theta {\text{d}}\theta = \frac{{(2k)!\pi }}{{{2^{2k + 1}}{{(k!)}^2}}}} \) \(\left( {{\rm{or}}\frac{{\left( \begin{array}{c}2k\\k\end{array} \right)\pi }}{{{2^{2k + 1}}}}} \right)\) A1
[3 marks]
Examiners report
Part a) has appeared several times before, though with it again being a ‘show that’ question, some candidates still need to be more aware of the need to show every step in their working, including the result that \(\sin ( – n\theta ) = – \sin (n\theta )\).
Part b) was usually answered correctly.
Part c) was again often answered correctly, though some candidates often less successfully utilised a trig-only approach rather than taking note of part b).
Part d) was a good source of marks for those who kept with the spirit of using complex numbers for this type of question. Some limited attempts at trig-only solutions were seen, and correct solutions using this approach were extremely rare.
Part e) was well answered, though numerical slips were often common. A small number integrated \(\sin n\theta \) as \(n\cos n\theta \).
A large number of candidates did not realise the help that part e) inevitably provided for part f). Some correctly expressed the volume as \(\pi \int {{{\cos }^4}x{\text{d}}x – \pi \int {{{\cos }^6}x{\text{d}}x} } \) and thus gained the first 2 marks but were able to progress no further. Only a small number of able candidates were able to obtain the correct answer of \(\frac{{{\pi ^2}}}{{32}}\).
[N/A]
Part g) proved to be a challenge for the vast majority, though it was pleasing to see some of the highest scoring candidates gain all 3 marks.
Question
Use the identity \(\cos 2\theta = 2{\cos ^2}\theta – 1\) to prove that \(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} ,{\text{ }}0 \leqslant x \leqslant \pi \).
Find a similar expression for \(\sin \frac{1}{2}x,{\text{ }}0 \leqslant x \leqslant \pi \).
Hence find the value of \(\int_0^{\frac{\pi }{2}} {\left( {\sqrt {1 + \cos x} + \sqrt {1 – \cos x} } \right){\text{d}}x} \).
Answer/Explanation
Markscheme
\(\cos x = 2{\cos ^2}\frac{1}{2}x – 1\)
\(\cos \frac{1}{2}x = \pm \sqrt {\frac{{1 + \cos x}}{2}} \) M1
positive as \(0 \leqslant x \leqslant \pi \) R1
\(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} \) AG
[2 marks]
\(\cos 2\theta = 1 – 2{\sin ^2}\theta \) (M1)
\(\sin \frac{1}{2}x = \sqrt {\frac{{1 – \cos x}}{2}} \) A1
[2 marks]
\(\sqrt 2 \int_0^{\frac{\pi }{2}} {\cos \frac{1}{2}x + \sin \frac{1}{2}x{\text{d}}x} \) A1
\( = \sqrt 2 \left[ {2\sin \frac{1}{2}x – 2\cos \frac{1}{2}x} \right]_0^{\frac{\pi }{2}}\) A1
\( = \sqrt 2 (0) – \sqrt 2 (0 – 2)\) A1
\( = 2\sqrt 2 \) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Show that \(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) for \(0 < \alpha < \frac{\pi }{2}\).
Hence find \(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x,{\text{ }}0 < \alpha < \frac{\pi }{2}} \).
Answer/Explanation
Markscheme
EITHER
use of a diagram and trig ratios
eg,
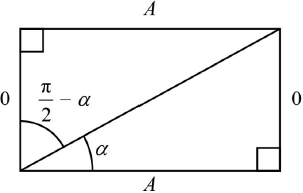
\(\tan \alpha = \frac{O}{A} \Rightarrow \cot \alpha = \frac{A}{O}\)
from diagram, \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{A}{O}\) R1
OR
use of \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} – \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} – \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) R1
THEN
\(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) AG
[1 mark]
\(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x} = [\arctan x]_{\tan \alpha }^{\cot \alpha }\) (A1)
Note: Limits (or absence of such) may be ignored at this stage.
\( = \arctan (\cot \alpha ) – \arctan (\tan \alpha )\) (M1)
\( = \frac{\pi }{2} – \alpha – \alpha \) (A1)
\( = \frac{\pi }{2} – 2\alpha \) A1
[4 marks]
Examiners report
This was generally well done.
This was generally well done. Some weaker candidates tried to solve part (b) through use of a substitution, though the standard result \(\arctan x\) was well known. A small number used \(\arctan x + c\) and went on to obtain an incorrect final answer.
Question
Consider the function \(f(x) = \frac{1}{{{x^2} + 3x + 2}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne – 2,{\text{ }}x \ne – 1\).
Express \({x^2} + 3x + 2\) in the form \({(x + h)^2} + k\).
Factorize \({x^2} + 3x + 2\).
Sketch the graph of \(f(x)\), indicating on it the equations of the asymptotes, the coordinates of the \(y\)-intercept and the local maximum.
Show that \(\frac{1}{{x + 1}} – \frac{1}{{x + 2}} = \frac{1}{{{x^2} + 3x + 2}}\).
Hence find the value of \(p\) if \(\int_0^1 {f(x){\text{d}}x = \ln (p)} \).
Sketch the graph of \(y = f\left( {\left| x \right|} \right)\).
Determine the area of the region enclosed between the graph of \(y = f\left( {\left| x \right|} \right)\), the \(x\)-axis and the lines with equations \(x = – 1\) and \(x = 1\).
Answer/Explanation
Markscheme
\({x^2} + 3x + 2 = {\left( {x + \frac{3}{2}} \right)^2} – \frac{1}{4}\) A1
[1 mark]
\({x^2} + 3x + 2 = (x + 2)(x + 1)\) A1
[1 mark]
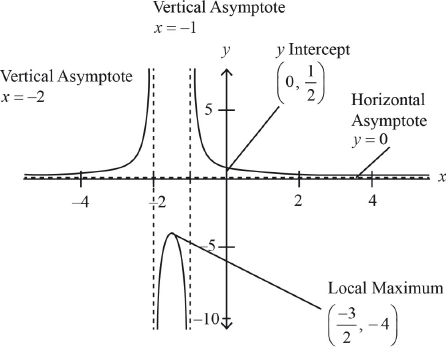
A1 for the shape
A1 for the equation \(y = 0\)
A1 for asymptotes \(x = – 2\) and \(x = – 1\)
A1 for coordinates \(\left( { – \frac{3}{2},{\text{ }} – 4} \right)\)
A1 \(y\)-intercept \(\left( {0,{\text{ }}\frac{1}{2}} \right)\)
[5 marks]
\(\frac{1}{{x + 1}} – \frac{1}{{x + 2}} = \frac{{(x + 2) – (x + 1)}}{{(x + 1)(x + 2)}}\) M1
\( = \frac{1}{{{x^2} + 3x + 2}}\) AG
[1 mark]
\(\int\limits_0^1 {\frac{1}{{x + 1}} – \frac{1}{{x + 2}}{\text{d}}x} \)
\( = \left[ {\ln (x + 1) – \ln (x + 2)} \right]_0^1\) A1
\( = \ln 2 – \ln 3 – \ln 1 + \ln 2\) M1
\( = \ln \left( {\frac{4}{3}} \right)\) M1A1
\(\therefore p = \frac{4}{3}\)
[4 marks]
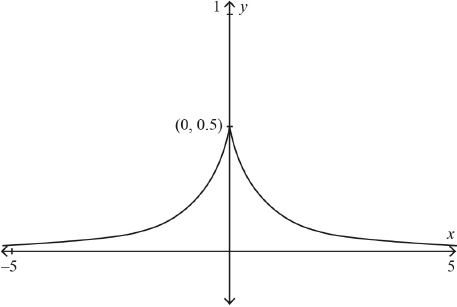
symmetry about the \(y\)-axis M1
correct shape A1
Note: Allow FT from part (b).
[2 marks]
\(2\int_0^1 {f(x){\text{d}}x} \) (M1)(A1)
\( = 2\ln \left( {\frac{4}{3}} \right)\) A1
Note: Do not award FT from part (e).
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Given that \(\int_{ – 2}^2 {f\left( x \right){\text{d}}x = 10} \) and \(\int_0^2 {f\left( x \right){\text{d}}x = 12} \), find
\(\int_{ – 2}^0 {\left( {f\left( x \right){\text{ + 2}}} \right){\text{d}}x} \).
\(\int_{ – 2}^0 {f\left( {x{\text{ + 2}}} \right){\text{d}}x} \).
Answer/Explanation
Markscheme
\(\int_{ – 2}^0 {f\left( x \right){\text{d}}x = 10} – 12 = – 2\) (M1)(A1)
\(\int_{ – 2}^0 {2{\text{d}}x = \left[ {2x} \right]} _{ – 2}^0 = 4\) A1
\(\int_{ – 2}^0 {\left( {f\left( x \right){\text{ + 2}}} \right){\text{d}}x} = 2\) A1
[4 marks]
\(\int_{ – 2}^0 {f\left( {x{\text{ + 2}}} \right){\text{d}}x} = \int_0^2 {f\left( x \right){\text{d}}x} \) (M1)
= 12 A1
[2 marks]
Examiners report
[N/A]
[N/A]
Question
Given that \(\int_{ – 2}^2 {f\left( x \right){\text{d}}x = 10} \) and \(\int_0^2 {f\left( x \right){\text{d}}x = 12} \), find
\(\int_{ – 2}^0 {\left( {f\left( x \right){\text{ + 2}}} \right){\text{d}}x} \).
\(\int_{ – 2}^0 {f\left( {x{\text{ + 2}}} \right){\text{d}}x} \).
Answer/Explanation
Markscheme
\(\int_{ – 2}^0 {f\left( x \right){\text{d}}x = 10} – 12 = – 2\) (M1)(A1)
\(\int_{ – 2}^0 {2{\text{d}}x = \left[ {2x} \right]} _{ – 2}^0 = 4\) A1
\(\int_{ – 2}^0 {\left( {f\left( x \right){\text{ + 2}}} \right){\text{d}}x} = 2\) A1
[4 marks]
\(\int_{ – 2}^0 {f\left( {x{\text{ + 2}}} \right){\text{d}}x} = \int_0^2 {f\left( x \right){\text{d}}x} \) (M1)
= 12 A1
[2 marks]
Examiners report
[N/A]
[N/A]
Question
Let \(y = {\text{arccos}}\left( {\frac{x}{2}} \right)\)
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Find \(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} \).
Answer/Explanation
Markscheme
\(y = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{{2\sqrt {1 – {{\left( {\frac{x}{2}} \right)}^2}} }}\left( { = – \frac{1}{{\sqrt {4 – {x^2}} }}} \right)\) M1A1
Note: M1 is for use of the chain rule.
[2 marks]
attempt at integration by parts M1
\(u = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}u}}{{{\text{d}}x}} = – \frac{1}{{\sqrt {4 – {x^2}} }}\)
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 1 \Rightarrow v = x\) (A1)
\(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} = \left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \int_0^1 {\frac{1}{{\sqrt {4 – {x^2}} }}} dx\) A1
using integration by substitution or inspection (M1)
\(\left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \left[ { – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}} \right]_0^1\) A1
Note: Award A1 for \({ – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}}\) or equivalent.
Note: Condone lack of limits to this point.
attempt to substitute limits into their integral M1
\( = \frac{\pi }{3} – \sqrt 3 + 2\) A1
[7 marks]
Examiners report
[N/A]
[N/A]
Question
Consider the functions \(f,\,\,g,\) defined for \(x \in \mathbb{R}\), given by \(f\left( x \right) = {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) and \(g\left( x \right) = {{\text{e}}^{ – x}}\,{\text{cos}}\,x\).
Find \(f’\left( x \right)\).
Find \(g’\left( x \right)\).
Hence, or otherwise, find \(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} \).
Answer/Explanation
Markscheme
attempt at product rule M1
\(f’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + {{\text{e}}^{ – x}}\,{\text{cos}}\,x\) A1
[2 marks]
\(g’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
[1 mark]
METHOD 1
Attempt to add \(f’\left( x \right)\) and \(g’\left( x \right)\) (M1)
\(f’\left( x \right) + g’\left( x \right) = – 2{{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
\(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} = \left[ { – \frac{{{{\text{e}}^{ – x}}}}{2}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)} \right]_0^\pi \) (or equivalent) A1
Note: Condone absence of limits.
\( = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)\) A1
METHOD 2
\(I = \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\( = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) OR \( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) M1A1
\( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\(I = \frac{1}{2}{{\text{e}}^{ – x}}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)\) A1
\(\int_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)} \) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
