Question: [Maximum mark: 20]
Consider the function f (x) = \(\sqrt{x^{2}-1}\), where 1 ≤ x ≤ 2.
(a) Sketch the curve y = f (x), clearly indicating the coordinates of the endpoints.
(b) (i) Show that the inverse function of f is given by f-1(x) = \(\sqrt{x^{2}+1}\).
(ii) State the domain and range of f -1.
The curve y = f (x) is rotated 2π about the y-axis to form a solid of revolution that is used to model a water container.
(c) (i) Show that the volume, Vm3, of water in the container when it is filled to a height of h metres is given by V = \(\pi \left ( \frac{1}{3}h^{3}+h \right )\).
(ii) Hence, determine the maximum volume of the container.
At t = 0, the container is empty. Water is then added to the container at a constant rate of 0.4m3 s-1.
(d) Find the time it takes to fill the container to its maximum volume.
(e) Find the rate of change of the height of the water when the container is filled to half its maximum volume.
▶️Answer/Explanation
Ans:
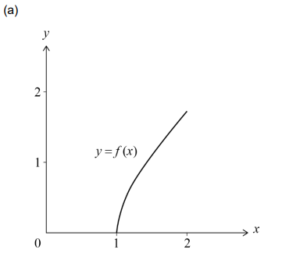
correct shape (concave down) within the given domain 1≤ x ≤ 2
(1, 0) and \(\left ( 2, \sqrt{3} \right )\) (=(2, 1.73))
Note: The coordinates of endpoints may be seen on the graph or marked on the axes.




Question
The region bounded by the curve \(y = \frac{{\ln (x)}}{x}\) and the lines x = 1, x = e, y = 0 is rotated through \(2\pi \) radians about the x-axis.
Find the volume of the solid generated.
▶️Answer/Explanation
Markscheme
METHOD 1
\(V = \pi \int_1^{\text{e}} {{{\left( {\frac{{\ln x}}{x}} \right)}^2}{\text{d}}x} \) M1
Integrating by parts:
\(u = {(\ln x)^2},{\text{ }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{1}{{{x^2}}}\) (M1)
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{{2\ln x}}{x},{\text{ }}v = – \frac{1}{x}\)
\( \Rightarrow V = \pi \left( { – \frac{{{{(\ln x)}^2}}}{x} + 2\int {\frac{{\ln x}}{{{x^2}}}{\text{d}}x} } \right)\) A1
\(u = \ln x,{\text{ }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{1}{{{x^2}}}\) (M1)
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{x},{\text{ }}v = – \frac{1}{x}\)
\(\therefore \int {\frac{{\ln x}}{{{x^2}}}{\text{d}}x = – \frac{{\ln x}}{x} + \int {\frac{1}{{{x^2}}}{\text{d}}x = – \frac{{\ln x}}{x} – \frac{1}{x}} } \) A1
\(\therefore V = \pi \left[ { – \frac{{{{(\ln x)}^2}}}{x} + 2\left( { – \frac{{\ln x}}{x} – \frac{1}{x}} \right)} \right]_1^{\text{e}}\)
\( = 2\pi – \frac{{5\pi }}{e}\) A1
[6 marks]
METHOD 2
\(V = \pi \int_1^{\text{e}} {{{\left( {\frac{{\ln x}}{x}} \right)}^2}{\text{d}}x} \) M1
Let \(\ln x = u \Rightarrow x = {{\text{e}}^u},{\text{ }}\frac{{{\text{d}}x}}{x} = {\text{d}}u\) (M1)
\(\int {{{\left( {\frac{{\ln x}}{x}} \right)}^2}{\text{d}}x = \int {\frac{{{u^2}}}{{{{\text{e}}^u}}}{\text{d}}u = \int {{{\text{e}}^{ – u}}} {u^2}{\text{d}}u = – {{\text{e}}^{ – u}}{u^2} + 2\int {{{\text{e}}^{ – u}}u{\text{d}}u} } } \) A1
\( = – {{\text{e}}^{ – u}}{u^2} + 2\left( { – {{\text{e}}^{ – u}}u + \int {{{\text{e}}^{ – u}}{\text{d}}u} } \right) = – {{\text{e}}^{ – u}}{u^2} – 2{{\text{e}}^{ – u}}u – 2{{\text{e}}^{ – u}}\)
\( = – {{\text{e}}^{ – u}}({u^2} + 2u + 2)\) A1
When x = e, u = 1. When x = 1, u = 0 .
\(\therefore {\text{ Volume}} = \pi \left[ { – {{\text{e}}^{ – u}}({u^2} + 2u + 2)} \right]_0^1\) M1
\( = \pi ( – 5{{\text{e}}^{ – 1}} + 2){\text{ }}\left( { = 2\pi – \frac{{5\pi }}{{\text{e}}}} \right)\) A1
[6 marks]
Examiners report
Only the best candidates were able to make significant progress with this question. It was disappointing to see that many candidates could not state that the formula for the required volume was \(\pi \int_1^e {{{\left( {\frac{{\ln x}}{x}} \right)}^2}{\text{d}}x} \) . Of those who could, very few either attempted integration by parts or used an appropriate substitution.
Question
Consider the part of the curve \(4{x^2} + {y^2} = 4\) shown in the diagram below.
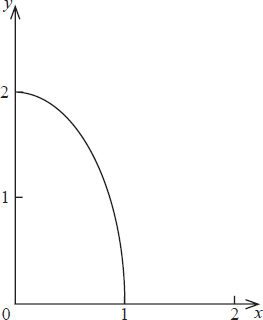
(a) Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of x and y .
(b) Find the gradient of the tangent at the point \(\left( {\frac{2}{{\sqrt 5 }},\frac{2}{{\sqrt 5 }}} \right)\).
(c) A bowl is formed by rotating this curve through \(2\pi \) radians about the x-axis.
Calculate the volume of this bowl.
▶️Answer/Explanation
Markscheme
(a) \(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1
Note: Award M1A0 for \(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4\) .
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{y}\) A1
(b) – 4 A1
(c) \(V = \int {\pi {y^2}{\text{d}}x} \) or equivalent M1
\(V = \pi \int_0^1 {(4 – 4{x^2}){\text{d}}x} \) A1
\( = \pi \left[ {4x – \frac{4}{3}{x^3}} \right]_0^1\) A1
\( = \frac{{8\pi }}{3}\) A1
Note: If it is correct except for the omission of \(\pi \) , award 2 marks.
[8 marks]
Examiners report
The first part of this question was done well by many, the only concern being the number that did not simplify the result from \( – \frac{{8x}}{{2y}}\). There were many variations on the formula for the volume in part c), the most common error being a multiple of \(2\pi \) rather than \(\pi \). On the whole this question was done well by many.
