Question
A particle moves in a straight line in a positive direction from a fixed point O.
The velocity v m \({{\text{s}}^{ – 1}}\) , at time t seconds, where \(t \geqslant 0\) , satisfies the differential equation
\[\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{ – v(1 + {v^2})}}{{50}}.\]
The particle starts from O with an initial velocity of 10 m \({{\text{s}}^{ – 1}}\) .
(a) (i) Express as a definite integral, the time taken for the particle’s velocity to decrease from 10 m \({{\text{s}}^{ – 1}}\) to 5 m \({{\text{s}}^{ – 1}}\) .
(ii) Hence calculate the time taken for the particle’s velocity to decrease from 10 m \({{\text{s}}^{ – 1}}\) to 5 m \({{\text{s}}^{ – 1}}\) .
(b) (i) Show that, when \(v > 0\) , the motion of this particle can also be described by the differential equation \(\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{ – (1 + {v^2})}}{{50}}\) where x metres is the displacement from O.
(ii) Given that v =10 when x = 0 , solve the differential equation expressing x in terms of v.
(iii) Hence show that \(v = \frac{{10 – \tan \frac{x}{{50}}}}{{1 + 10\tan \frac{x}{{50}}}}\).
Answer/Explanation
Markscheme
(a) (i) EITHER
Attempting to separate the variables (M1)
\(\frac{{{\text{d}}v}}{{ – v(1 + {v^2})}} = \frac{{{\text{d}}t}}{{50}}\) (A1)
OR
Inverting to obtain \(\frac{{{\text{d}}t}}{{{\text{d}}v}}\) (M1)
\(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{{ – 50}}{{v(1 + {v^2})}}\) (A1)
THEN
\(t = – 50\int_{10}^5 {\frac{1}{{v(1 + {v^2})}}} {\text{d}}v\,\,\,\,\,\left( { = 50\int_5^{10} {\frac{1}{{v(1 + {v^2})}}{\text{d}}v} } \right)\) A1 N3
(ii) \(t = 0.732{\text{ (sec)}}\,\,\,\,\,\left( { = 25\ln \frac{{104}}{{101}}(\sec )} \right)\) A2 N2
[5 marks]
(b) (i) \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = v\frac{{{\text{d}}v}}{{{\text{d}}x}}\) (M1)
Must see division by v \((v > 0)\) A1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{ – (1 + {v^2})}}{{50}}\) AG N0
(ii) Either attempting to separate variables or inverting to obtain \(\frac{{{\text{d}}x}}{{{\text{d}}v}}\) (M1)
\({\frac{{{\text{d}}v}}{{1 + {v^2}}} = – \frac{1}{{50}}\int {{\text{d}}x} }\) (or equivalent) A1
Attempting to integrate both sides M1
\(\arctan v = – \frac{x}{{50}} + C\) A1A1
Note: Award A1 for a correct LHS and A1 for a correct RHS that must include C.
When \(x = 0{\text{ , }}v = 10{\text{ and so }}C = \arctan 10\) M1
\(x = 50(\arctan 10 – \arctan v)\) A1 N1
(iii) Attempting to make \(\arctan v\) the subject. M1
\(\arctan v = \arctan 10 – \frac{x}{{50}}\) A1
\(v = \tan \left( {\arctan 10 – \frac{x}{{50}}} \right)\) M1A1
Using tan(A − B) formula to obtain the desired form. M1
\(v = \frac{{10 – \tan \frac{x}{{50}}}}{{1 + 10\tan \frac{x}{{50}}}}\) AG N0
[14 marks]
Total [19 marks]
Examiners report
No comment.
Question
A body is moving through a liquid so that its acceleration can be expressed as
\[\left( { – \frac{{{v^2}}}{{200}} – 32} \right){\text{m}}{{\text{s}}^{ – 2}},\]
where \(v{\text{ m}}{{\text{s}}^{ – 1}}\) is the velocity of the body at time t seconds.
The initial velocity of the body was known to be \(40{\text{ m}}{{\text{s}}^{ – 1}}\).
(a) Show that the time taken, T seconds, for the body to slow to \(V{\text{ m}}{{\text{s}}^{ – 1}}\) is given by
\[T = 200\int_V^{40} {\frac{1}{{{v^2} + {{80}^2}}}{\text{d}}v.} \]
(b) (i) Explain why acceleration can be expressed as \(v\frac{{{\text{d}}v}}{{{\text{d}}s}}\), where s is displacement, in metres, of the body at time t seconds.
(ii) Hence find a similar integral to that shown in part (a) for the distance, S metres, travelled as the body slows to \(V{\text{ m}}{{\text{s}}^{ – 1}}\).
(c) Hence, using parts (a) and (b), find the distance travelled and the time taken until the body momentarily comes to rest.
Answer/Explanation
Markscheme
(a) \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = – \frac{{{v^2}}}{{200}} – 32\left( { = \frac{{ – {v^2} – 6400}}{{200}}} \right)\) (M1)
\(\int_0^T {{\text{d}}t = \int_{40}^V { – \frac{{200}}{{{v^2} + {{80}^2}}}{\text{d}}v} } \) M1A1A1
\(T = 200\int_V^{40} {\frac{1}{{{v^2} + {{80}^2}}}{\text{d}}v} \) AG
[4 marks]
(b) (i) \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}v}}{{{\text{d}}s}} \times \frac{{{\text{d}}s}}{{{\text{d}}t}}\) R1
\( = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\) AG
(ii) \(v\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{{ – {v^2} – {{80}^2}}}{{200}}\) (M1)
\(\int_0^S {{\text{d}}s = \int_{40}^V -{\frac{{200v}}{{{v^2} + {{80}^2}}}{\text{d}}v} } \) M1A1A1
\(\int_0^S {{\text{d}}s = \int_V^{40} {\frac{{200v}}{{{v^2} + {{80}^2}}}{\text{d}}v} } \) M1
\(S = 200\int_V^{40} {\frac{v}{{{v^2} + {{80}^2}}}{\text{d}}v} \) A1
[7 marks]
(c) letting V = 0 (M1)
distance \( = 200\int_0^{40} {\frac{v}{{{v^2} + {{80}^2}}}{\text{d}}v = 22.3{\text{ metres}}} \) A1
time \( = 200\int_0^{40} {\frac{1}{{{v^2} + {{80}^2}}}{\text{d}}v = 1.16{\text{ seconds}}} \) A1
[3 marks]
Total [14 marks]
Examiners report
Many students failed to understand the problem as one of solving differential equations. In addition there were many problems seen in finding the end points for the definite integrals. Part (b) (i) should have been a simple point having used the chain rule, but it seemed that many students had not seen this, even though it is clearly in the syllabus.
Question
A jet plane travels horizontally along a straight path for one minute, starting at time \(t = 0\) , where \(t\) is measured in seconds. The acceleration, \(a\) , measured in ms−2, of the jet plane is given by the straight line graph below.
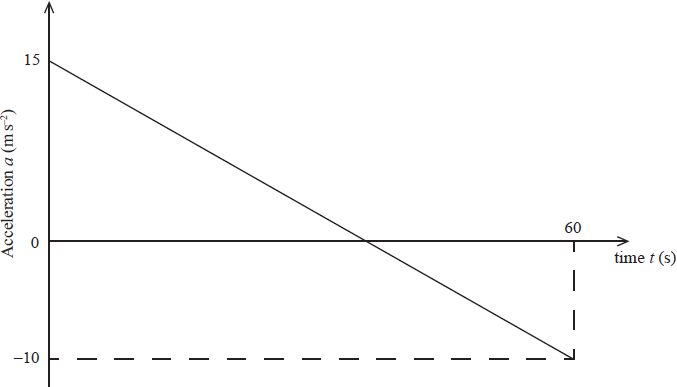
Find an expression for the acceleration of the jet plane during this time, in terms of \(t\) .
Given that when \(t = 0\) the jet plane is travelling at \(125\) ms−1, find its maximum velocity in ms−1 during the minute that follows.
Given that the jet plane breaks the sound barrier at \(295\) ms−1, find out for how long the jet plane is travelling greater than this speed.
Answer/Explanation
Markscheme
equation of line in graph \(a = – \frac{{25}}{{60}}t + 15\) A1
\(\left( {a = – \frac{5}{{12}}t + 15} \right)\)
[1 mark]
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = – \frac{5}{{12}}t + 15\) (M1)
\(v = – \frac{5}{{24}}{t^2} + 15t + c\) (A1)
when \(t = 0\) , \(v = 125\) ms−1
\(v = – \frac{5}{{24}}{t^2} + 15t + 125\) A1
from graph or by finding time when \(a = 0\)
maximum \(= 395\) ms−1 A1
[4 marks]
EITHER
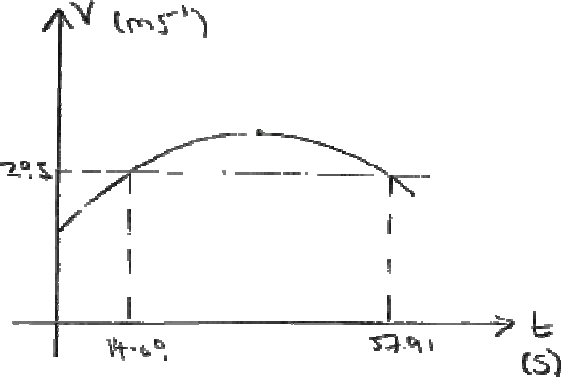
graph drawn and intersection with \(v = 295\) ms−1 (M1)(A1)
\(t = 57.91 – 14.09 = 43.8\) A1
OR
\(295 = – \frac{5}{{24}}{t^2} + 15t + 125 \Rightarrow t = 57.91…\); \(14.09…\)
\(t = 57.91… – 14.09… = 43.8\left( {8\sqrt {30} } \right)\) A1
[3 marks]
Examiners report
This question was well answered by a large number of candidates and indicated a good understanding of calculus, kinematics and use of the graphing calculator. Some candidates worked in \(x\) and \(y\) rather than \(a\), \(v\) and \(t\) but mostly obtained correct solutions. Although the majority of candidate used integration throughout the question some correct solutions were obtained by considering the areas in the diagram.
This question was well answered by a large number of candidates and indicated a good understanding of calculus, kinematics and use of the graphing calculator. Some candidates worked in \(x\) and \(y\) rather than \(a\), \(v\) and \(t\) but mostly obtained correct solutions. Although the majority of candidate used integration throughout the question some correct solutions were obtained by considering the areas in the diagram.
This question was well answered by a large number of candidates and indicated a good understanding of calculus, kinematics and use of the graphing calculator. Some candidates worked in \(x\) and \(y\) rather than \(a\), \(v\) and \(t\) but mostly obtained correct solutions. Although the majority of candidate used integration throughout the question some correct solutions were obtained by considering the areas in the diagram.
Question
A skydiver jumps from a stationary balloon at a height of 2000 m above the ground.
Her velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\) , t seconds after jumping, is given by \(v = 50(1 – {{\text{e}}^{ – 0.2t}})\) .
Find her acceleration 10 seconds after jumping.
How far above the ground is she 10 seconds after jumping?
Answer/Explanation
Markscheme
\(a = 10{{\text{e}}^{ – 0.2t}}\) (M1)(A1)
at \(t = 10\) , \(a = 1.35{\text{ }}({\text{m}}{{\text{s}}^{ – 2}})\,\,\,\,\,{\text{(accept }}10{e^{ – 2}})\) A1
[3 marks]
METHOD 1
\(d = \int_0^{10} {50(1 – {{\text{e}}^{ – 0.2t}}){\text{d}}t} \) (M1)
\( = 283.83…\) A1
so distance above ground \( = 1720{\text{ (m) (3 sf) }}\left( {{\text{accept 1716 (m)}}} \right)\) A1
METHOD 2
\({\text{s}} = \int {50(1 – {{\text{e}}^{ – 0.2t}}){\text{d}}t = 50t + 250{{\text{e}}^{ – 0.2t}}( + c)} \) M1
Taking s = 0 when t = 0 gives c = −250 M1
So when t = 10, s = 283.3…
so distance above ground \( = 1720{\text{ (m) (3 sf) }}\left( {{\text{accept 1716 (m)}}} \right)\) A1
[3 marks]
Examiners report
Part (a) was generally correctly answered. A few candidates suffered the Arithmetic Penalty for giving their answer to more than 3sf. A smaller number were unable to differentiate the exponential function correctly. Part (b) was less well answered, many candidates not thinking clearly about the position and direction associated with the initial conditions.
Part (a) was generally correctly answered. A few candidates suffered the Arithmetic Penalty for giving their answer to more than 3sf. A smaller number were unable to differentiate the exponential function correctly. Part (b) was less well answered, many candidates not thinking clearly about the position and direction associated with the initial conditions.
Question
A particle moves in a straight line with velocity v metres per second. At any time t seconds, \(0 \leqslant t < \frac{{3\pi }}{4}\), the velocity is given by the differential equation \(\frac{{{\text{d}}v}}{{{\text{d}}t}} + {v^2} + 1 = 0\) .
It is also given that v = 1 when t = 0 .
Find an expression for v in terms of t .
Sketch the graph of v against t , clearly showing the coordinates of any intercepts, and the equations of any asymptotes.
(i) Write down the time T at which the velocity is zero.
(ii) Find the distance travelled in the interval [0, T] .
Find an expression for s , the displacement, in terms of t , given that s = 0 when t = 0 .
Hence, or otherwise, show that \(s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = – {v^2} – 1\)
attempt to separate the variables M1
\(\int {\frac{1}{{1 + {v^2}}}{\text{d}}v = \int { – 1{\text{d}}t} } \) A1
\(\arctan v = – t + k\) A1A1
Note: Do not penalize the lack of constant at this stage.
when t = 0, v = 1 M1
\( \Rightarrow k = \arctan 1 = \left( {\frac{\pi }{4}} \right) = (45^\circ )\) A1
\( \Rightarrow v = \tan \left( {\frac{\pi }{4} – t} \right)\) A1
[7 marks]
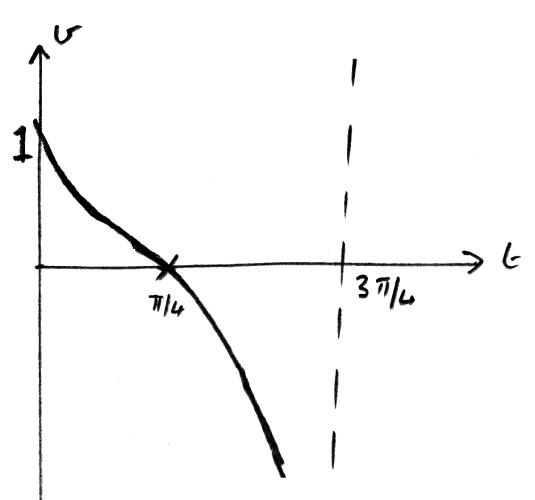A1A1A1
Note: Award A1 for general shape,
A1 for asymptote,
A1 for correct t and v intercept.
Note: Do not penalise if a larger domain is used.
[3 marks]
(i) \(T = \frac{\pi }{4}\) A1
(ii) area under curve \( = \int_0^{\frac{\pi }{4}} {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) (M1)
\( = 0.347\left( { = \frac{1}{2}\ln 2} \right)\) A1
[3 marks]
\(v = \tan \left( {\frac{\pi }{4} – t} \right)\)
\(s = \int {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) M1
\(\int {\frac{{\sin \left( {\frac{\pi }{4} – t} \right)}}{{\cos \left( {\frac{\pi }{4} – t} \right)}}} {\text{ d}}t\) (M1)
\( = \ln \cos \left( {\frac{\pi }{4} – t} \right) + k\) A1
when \(t = 0,{\text{ }}s = 0\)
\(k = – \ln \cos \frac{\pi }{4}\) A1
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\left( { = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – t} \right)} \right]} \right)\) A1
[5 marks]
METHOD 1
\(\frac{\pi }{4} – t = \arctan v\) M1
\(t = \frac{\pi }{4} – \arctan v\)
\(s = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – \frac{\pi }{4} + \arctan v} \right)} \right]\)
\(s = \ln \left[ {\sqrt 2 \cos (\arctan v)} \right]\) M1A1
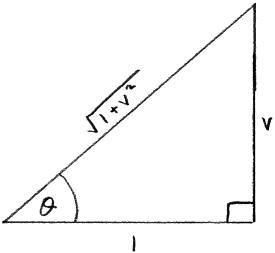
\(s = \ln \left[ {\sqrt 2 \cos \left( {\arccos \frac{1}{{\sqrt {1 + {v^2}} }}} \right)} \right]\) A1
\( = \ln \frac{{\sqrt 2 }}{{\sqrt {1 + {v^2}} }}\)
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 2
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\)
\( = – \ln \sec \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {{\tan }^2}\left( {\frac{\pi }{4} – t} \right)} – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {v^2}} – \ln \cos \frac{\pi }{4}\) A1
\( = \ln \frac{1}{{\sqrt {1 + {v^2}} }} + \ln \sqrt 2 \) A1
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 3
\(v\frac{{dv}}{{ds}} = – {v^2} – 1\) M1
\(\int {\frac{v}{{{v^2} + 1}}dv = – \int {1ds} } \) M1
\(\frac{1}{2}\ln ({v^2} + 1) = – s + k\) A1
when \(s = 0\,,{\text{ }}t = 0 \Rightarrow v = 1\)
\( \Rightarrow k = \frac{1}{2}\ln 2\) A1
\( \Rightarrow s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
[4 marks]
Examiners report
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
Question
A particle moves along a straight line so that after t seconds its displacement s , in metres, satisfies the equation \({s^2} + s – 2t = 0\) . Find, in terms of s , expressions for its velocity and its acceleration.
Answer/Explanation
Markscheme
\(2s\frac{{{\text{d}}s}}{{{\text{d}}t}} + \frac{{{\text{d}}s}}{{{\text{d}}t}} – 2 = 0\) M1A1
\(v = \frac{{{\text{d}}s}}{{{\text{d}}t}} = \frac{2}{{2s + 1}}\) A1
EITHER
\(a = \frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}v}}{{{\text{d}}s}}\frac{{{\text{d}}s}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{{ – 4}}{{{{(2s + 1)}^2}}}\) (A1)
\(a = \frac{{ – 4}}{{{{(2s + 1)}^2}}}\frac{{{\text{d}}s}}{{{\text{d}}t}}\)
OR
\(2{\left( {\frac{{{\text{d}}s}}{{{\text{d}}t}}} \right)^2} + 2s\frac{{{{\text{d}}^2}s}}{{{\text{d}}{t^2}}} + \frac{{{{\text{d}}^2}s}}{{{\text{d}}{t^2}}} = 0\) (M1)
\(\frac{{{{\text{d}}^2}s}}{{\underbrace {{\text{d}}{t^2}}_a}} = \frac{{ – 2{{\left( {\frac{{{\text{d}}s}}{{{\text{d}}t}}} \right)}^2}}}{{2s + 1}}\) (A1)
THEN
\(a = \frac{{ – 8}}{{{{(2s + 1)}^3}}}\) A1
[6 marks]
Examiners report
Despite the fact that many candidates were able to calculate the speed of the particle, many of them failed to calculate the acceleration. Implicit differentiation turned out to be challenging in this exercise showing in many cases a lack of understanding of independent/dependent variables. Very often candidates did not use the chain rule or implicit differentiation when attempting to find the acceleration. It was not uncommon to see candidates trying to differentiate implicitly with respect to t rather than s, but getting the variables muddled.
Question
A particle, A, is moving along a straight line. The velocity, \({v_A}{\text{ m}}{{\text{s}}^{ – 1}}\), of A t seconds after its motion begins is given by
\[{v_A} = {t^3} – 5{t^2} + 6t.\]
Sketch the graph of \({v_A} = {t^3} – 5{t^2} + 6t\) for \(t \geqslant 0\), with \({v_A}\) on the vertical axis and t on the horizontal. Show on your sketch the local maximum and minimum points, and the intercepts with the t-axis.
Write down the times for which the velocity of the particle is increasing.
Write down the times for which the magnitude of the velocity of the particle is increasing.
At t = 0 the particle is at point O on the line.
Find an expression for the particle’s displacement, \({x_A}{\text{m}}\), from O at time t.
A second particle, B, moving along the same line, has position \({x_B}{\text{ m}}\), velocity \({v_B}{\text{ m}}{{\text{s}}^{ – 1}}\) and acceleration, \({a_B}{\text{ m}}{{\text{s}}^{ – 2}}\), where \({a_B} = – 2{v_B}\) for \(t \geqslant 0\). At \(t = 0,{\text{ }}{x_B} = 20\) and \({v_B} = – 20\).
Find an expression for \({v_B}\) in terms of t.
Find the value of t when the two particles meet.
Answer/Explanation
Markscheme
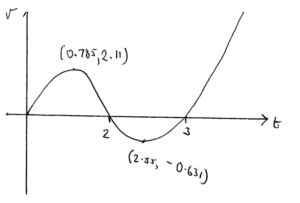A1A1A1
Note: Award A1 for general shape, A1 for correct maximum and minimum, A1 for intercepts.
Note: Follow through applies to (b) and (c).
[3 marks]
\(0 \leqslant t < 0.785,{\text{ }}\left( {{\text{or }}0 \leqslant t < \frac{{5 – \sqrt 7 }}{3}} \right)\) A1
(allow \(t < 0.785\))
and \(t > 2.55{\text{ }}\left( {{\text{or }}t > \frac{{5 + \sqrt 7 }}{3}} \right)\) A1
[2 marks]
\(0 \leqslant t < 0.785,{\text{ }}\left( {{\text{or }}0 \leqslant t < \frac{{5 – \sqrt 7 }}{3}} \right)\) A1
(allow \(t < 0.785\))
\(2 < t < 2.55,{\text{ }}\left( {{\text{or }}2 < t < \frac{{5 + \sqrt 7 }}{3}} \right)\) A1
\(t > 3\) A1
[3 marks]
position of A: \({x_A} = \int {{t^3} – 5{t^2} + 6t{\text{ d}}t} \) (M1)
\({x_A} = \frac{1}{4}{t^4} – \frac{5}{3}{t^3} + 3{t^2}\,\,\,\,\,( + c)\) A1
when \(t = 0,{\text{ }}{x_A} = 0\), so \(c = 0\) R1
[3 marks]
\(\frac{{{\text{d}}{v_B}}}{{{\text{d}}t}} = – 2{v_B} \Rightarrow \int {\frac{1}{{{v_B}}}{\text{d}}{v_B} = \int { – 2{\text{d}}t} } \) (M1)
\(\ln \left| {{v_B}} \right| = – 2t + c\) (A1)
\({v_B} = A{e^{ – 2t}}\) (M1)
\({v_B} = – 20\) when t = 0 so \({v_B} = – 20{e^{ – 2t}}\) A1
[4 marks]
\({x_B} = 10{e^{ – 2t}}( + c)\) (M1)(A1)
\({x_B} = 20{\text{ when }}t = 0{\text{ so }}{x_B} = 10{e^{ – 2t}} + 10\) (M1)A1
meet when \(\frac{1}{4}{t^4} – \frac{5}{3}{t^3} + 3{t^2} = 10{e^{ – 2t}} + 10\) (M1)
\(t = 4.41(290 \ldots )\) A1
[6 marks]
Examiners report
Part (a) was generally well done, although correct accuracy was often a problem.
Parts (b) and (c) were also generally quite well done.
Parts (b) and (c) were also generally quite well done.
A variety of approaches were seen in part (d) and many candidates were able to obtain at least 2 out of 3. A number missed to consider the \(+c\) , thereby losing the last mark.
Surprisingly few candidates were able to solve part (e) correctly. Very few could recognise the easy variable separable differential equation. As a consequence part (f) was frequently left.
Surprisingly few candidates were able to solve part (e) correctly. Very few could recognise the easy variable separable differential equation. As a consequence part (f) was frequently left.
Question
The acceleration of a car is \(\frac{1}{{40}}(60 – v){\text{ m}}{{\text{s}}^{ – 2}}\), when its velocity is \(v{\text{ m}}{{\text{s}}^{ – 2}}\). Given the car starts from rest, find the velocity of the car after 30 seconds.
Answer/Explanation
Markscheme
METHOD 1
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{1}{{40}}(60 – v)\) (M1)
attempting to separate variables \(\int {\frac{{{\text{d}}v}}{{60 – v}} = \int {\frac{{{\text{d}}t}}{{40}}} } \) M1
\( – \ln (60 – v) = \frac{t}{{40}} + c\) A1
\(c = – \ln 60\) (or equivalent) A1
attempting to solve for v when t = 30 (M1)
\(v = 60 – 60{e^{ – \frac{3}{4}}}\)
\(v = 31.7{\text{ (m}}{{\text{s}}^{ – 1}})\) A1
METHOD 2
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{1}{{40}}(60 – v)\) (M1)
\(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{{40}}{{60 – v}}\) (or equivalent) M1
\(\int_0^{{v_f}} {\frac{{40}}{{60 – v}}{\text{d}}v = 30} \) where \({v_f}\) is the velocity of the car after 30 seconds. A1A1
attempting to solve \(\int_0^{{v_f}} {\frac{{40}}{{60 – v}}{\text{d}}v = 30} \) for \({v_f}\) (M1)
\(v = 31.7{\text{ (m}}{{\text{s}}^{ – 1}})\) A1
[6 marks]
Examiners report
Most candidates experienced difficulties with this question. A large number of candidates did not attempt to separate the variables and instead either attempted to integrate with respect to v or employed constant acceleration formulae. Candidates that did separate the variables and attempted to integrate both sides either made a sign error, omitted the constant of integration or found an incorrect value for this constant. Almost all candidates were not aware that this question could be solved readily on a GDC.
Question
Particle A moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ – 1}}\), at time t seconds, is given by \(v(t) = \frac{t}{{12 + {t^4}}},{\text{ }}t \geqslant 0\).
Particle B moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ – 1}}\) is related to its displacement \(s{\text{ m}}\), by the equation \(v(s) = \arcsin \left( {\sqrt s } \right)\).
Sketch the graph of \(y = v(t)\). Indicate clearly the local maximum and write down its coordinates.
Use the substitution \(u = {t^2}\) to find \(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t} \).
Find the exact distance travelled by particle \(A\) between \(t = 0\) and \(t = 6\) seconds.
Give your answer in the form \(k\arctan (b),{\text{ }}k,{\text{ }}b \in \mathbb{R}\).
Find the acceleration of particle B when \(s = 0.1{\text{ m}}\).
Answer/Explanation
Markscheme
(a)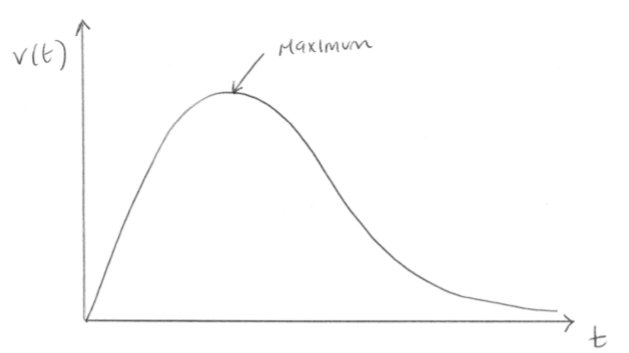
A1
A1 for correct shape and correct domain
\((1.41,{\text{ }}0.0884){\text{ }}\left( {\sqrt 2 ,{\text{ }}\frac{{\sqrt 2 }}{{16}}} \right)\) A1
[2 marks]
EITHER
\(u = {t^2}\)
\(\frac{{{\text{d}}u}}{{{\text{d}}t}} = 2t\) A1
OR
\(t = {u^{\frac{1}{2}}}\)
\(\frac{{{\text{d}}t}}{{{\text{d}}u}} = \frac{1}{2}{u^{ – \frac{1}{2}}}\) A1
THEN
\(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t = \frac{1}{2}\int {\frac{{{\text{d}}u}}{{12 + {u^2}}}} } \) M1
\( = \frac{1}{{2\sqrt {12} }}\arctan \left( {\frac{u}{{\sqrt {12} }}} \right)( + c)\) M1
\( = \frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)( + c)\) or equivalent A1
[4 marks]
\(\int_0^6 {\frac{t}{{12 + {t^4}}}{\text{d}}t} \) (M1)
\( = \left[ {\frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)} \right]_0^6\) M1
\( = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{36}}{{2\sqrt 3 }}} \right)} \right){\text{ }}\left( { = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{18}}{{\sqrt 3 }}} \right)} \right)} \right){\text{ (m)}}\) A1
Note: Accept \(\frac{{\sqrt 3 }}{{12}}\arctan \left( {6\sqrt 3 } \right)\) or equivalent.
[3 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{1}{{2\sqrt {s(1 – s)} }}\) (A1)
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\)
\(a = \arcsin \left( {\sqrt s } \right) \times \frac{1}{{2\sqrt {s(1 – s)} }}\) (M1)
\(a = \arcsin \left( {\sqrt {0.1} } \right) \times \frac{1}{{2\sqrt {0.1 \times 0.9} }}\)
\(a = 0.536{\text{ (m}}{{\text{s}}^{ – 2}})\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
A particle moves in a straight line such that its velocity, \(v\,{\text{m}}\,{{\text{s}}^{ – 1}}\) , at time t seconds, is given by
\(v(t) = \left\{ {\begin{array}{*{20}{c}} {5 – {{(t – 2)}^2},}&{0 \le t \le 4} \\ {3 – \frac{t}{2},}&{t > 4} \end{array}.} \right.\)
Find the value of \(t\) when the particle is instantaneously at rest.
The particle returns to its initial position at \(t = T\).
Find the value of T.
Answer/Explanation
Markscheme
\(3 – \frac{t}{2} = 0 \Rightarrow t = 6{\text{ (s)}}\) (M1)A1
Note: Award A0 if either \(t = – 0.236\) or \(t = 4.24\) or both are stated with \(t = 6\).
[2 marks]
let \(d\) be the distance travelled before coming to rest
\(d = \int_0^4 {5 – {{(t – 2)}^2}{\text{d}}t + \int_4^6 {3 – \frac{t}{2}{\text{d}}t} } \) (M1)(A1)
Note: Award M1 for two correct integrals even if the integration limits are incorrect. The second integral can be specified as the area of a triangle.
\(d = \frac{{47}}{3}\;\;\;( = 15.7){\text{ (m)}}\) (A1)
attempting to solve \(\int_6^T {\left( {\frac{t}{2} – 3} \right){\text{d}}t = \frac{{47}}{3}} \) (or equivalent) for \(T\) M1
\(T = 13.9{\text{ (s)}}\) A1
[5 marks]
Total [7 marks]
Examiners report
Part (a) was not done as well as expected. A large number of candidates attempted to solve \(5 – {(t – 2)^2} = 0\) for \(t\). Some candidates attempted to find when the particle’s acceleration was zero.
Most candidates had difficulty with part (b) with a variety of errors committed. A significant proportion of candidates did not understand what was required. Many candidates worked with indefinite integrals rather than with definite integrals. Only a small percentage of candidates started by correctly finding the distance travelled by the particle before coming to rest. The occasional candidate made adroit use of a GDC and found the correct value of \(t\) by finding where the graph of \(\int_0^4 {5 – {{(t – 2)}^2}{\text{d}}t + \int_4^x {3 – \frac{t}{2}{\text{d}}t} } \) crossed the horizontal axis.
Question
Richard, a marine soldier, steps out of a stationary helicopter, 1000 m above the ground, at time \(t = 0\). Let his height, in metres, above the ground be given by \(s(t)\). For the first 10 seconds his velocity, \(v(t){\text{m}}{{\text{s}}^{ – 1}}\), is given by \(v(t) = – 10t\).
(i) Find his acceleration \(a(t)\) for \(t < 10\).
(ii) Calculate \(v(10)\).
(iii) Show that \(s(10) = 500\).
At \(t = 10\) his parachute opens and his acceleration \(a(t)\) is subsequently given by \(a(t) = – 10 – 5v,{\text{ }}t \ge 10\).
Given that \(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{1}{{\frac{{{\text{d}}v}}{{{\text{d}}t}}}}\), write down \(\frac{{{\text{d}}t}}{{{\text{d}}v}}\) in terms of \(v\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Hence show that \(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Hence find an expression for the velocity, \(v\), for \(t \ge 10\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Find an expression for his height, \(s\), above the ground for \(t \ge 10\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Find the value of \(t\) when Richard lands on the ground.
Answer/Explanation
Markscheme
(i) \(a(t) = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – 10{\text{ (m}}{{\text{s}}^{ – 2}}{\text{)}}\) A1
(ii) \(t = 10 \Rightarrow v = – 100{\text{ (m}}{{\text{s}}^{ – 1}}{\text{)}}\) A1
(iii) \(s = \int { – 10t{\text{d}}t = – 5{t^2}( + c)} \) M1A1
\(s = 1000{\text{ for }}t = 0 \Rightarrow c = 1000\) (M1)
\(s = – 5{t^2} + 1000\) A1
at \(t = 10,{\text{ }}s = 500{\text{ (m)}}\) AG
Note: Accept use of definite integrals.
[6 marks]
\(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{1}{{( – 10 – 5v)}}\) A1
[1 mark]
METHOD 1
\(t = \int {\frac{1}{{ – 10 – 5v}}{\text{d}}v = – \frac{1}{5}\ln ( – 10 – 5v)( + c)} \) M1A1
Note: Accept equivalent forms using modulus signs.
\(t = 10,{\text{ }}v = – 100\)
\(10 = – \frac{1}{5}\ln (490) + c\) M1
\(c = 10 + \frac{1}{5}\ln (490)\) A1
\(t = 10 + \frac{1}{5}\ln 490 – \frac{1}{5}\ln ( – 10 – 5v)\) A1
Note: Accept equivalent forms using modulus signs.
\(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\) AG
Note: Accept use of definite integrals.
METHOD 2
\(t = \int {\frac{1}{{ – 10 – 5v}}{\text{d}}v = – \frac{1}{5}\int {\frac{1}{{2 + v}}{\text{d}}v = – \frac{1}{5}\ln \left| {2 + v} \right|( + c)} } \) M1A1
Note: Accept equivalent forms.
\(t = 10,{\text{ }}v = – 100\)
\(10 = – \frac{1}{5}\ln \left| { – 98} \right| + c\) M1
Note: If \(\ln ( – 98)\) is seen do not award further A marks.
\(c = 10 + \frac{1}{5}\ln 98\) A1
\(t = 10 + \frac{1}{5}\ln 98 – \frac{1}{5}\ln \left| {2 + v} \right|\) A1
Note: Accept equivalent forms.
\(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\) AG
Note: Accept use of definite integrals.
[5 marks]
\(5(t – 10) = \ln \frac{{98}}{{( – 2 – v)}}\)
\(\frac{{2 + v}}{{98}} = – {{\text{e}}^{ – 5(t – 10)}}\) (M1)
\(v = – 2 – 98{{\text{e}}^{ – 5(t – 10)}}\) A1
[2 marks]
\(\frac{{{\text{d}}s}}{{{\text{d}}t}} = – 2 – 98{{\text{e}}^{ – 5(t – 10)}}\)
\(s = – 2t + \frac{{98}}{5}{{\text{e}}^{ – 5(t – 10)}}( + k)\) M1A1
at \(t = 10,{\text{ }}s = 500 \Rightarrow 500 = – 20 + \frac{{98}}{5} + k \Rightarrow k = 500.4\) M1A1
\(s = – 2t + \frac{{98}}{5}{{\text{e}}^{ – 5(t – 10)}} + 500.4\) A1
Note: Accept use of definite integrals.
[5 marks]
\(t = 250{\text{ for }}s = 0\) (M1)A1
[2 marks]
Total [21 marks]
Examiners report
Parts (i) and (ii) were well answered by most candidates.
In (iii) the constant of integration was often forgotten. Most candidates calculated the displacement and then used different strategies, mostly incorrect, to remove the negative sign from \( – 500\).
Surprisingly part (b) was not well done as the question stated the method. Many candidates simply wrote down \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\) while others seemed unaware that \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\) was the acceleration.
Part (c) was not always well done as it followed from (b) and at times there was very little to allow follow through. Once again some candidates started with what they were trying to prove. Among the candidates that attempted to integrate many did not consider the constant of integration properly.
In part (d) many candidates ignored the answer given in (c) and attempted to manipulate different expressions.
Part (e) was poorly answered: the constant of integration was often again forgotten and some inappropriate uses of Physics formulas assuming that the acceleration was constant were used. There was unclear thinking with the two sides of an equation being integrated with respect to different variables.
Although part (e) was often incorrect, some follow through marks were gained in part (f).
Question
Richard, a marine soldier, steps out of a stationary helicopter, 1000 m above the ground, at time \(t = 0\). Let his height, in metres, above the ground be given by \(s(t)\). For the first 10 seconds his velocity, \(v(t){\text{m}}{{\text{s}}^{ – 1}}\), is given by \(v(t) = – 10t\).
(i) Find his acceleration \(a(t)\) for \(t < 10\).
(ii) Calculate \(v(10)\).
(iii) Show that \(s(10) = 500\).
At \(t = 10\) his parachute opens and his acceleration \(a(t)\) is subsequently given by \(a(t) = – 10 – 5v,{\text{ }}t \ge 10\).
Given that \(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{1}{{\frac{{{\text{d}}v}}{{{\text{d}}t}}}}\), write down \(\frac{{{\text{d}}t}}{{{\text{d}}v}}\) in terms of \(v\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Hence show that \(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Hence find an expression for the velocity, \(v\), for \(t \ge 10\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Find an expression for his height, \(s\), above the ground for \(t \ge 10\).
You are told that Richard’s acceleration, \(a(t) = – 10 – 5v\), is always positive, for \(t \ge 10\).
Find the value of \(t\) when Richard lands on the ground.
Answer/Explanation
Markscheme
(i) \(a(t) = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – 10{\text{ (m}}{{\text{s}}^{ – 2}}{\text{)}}\) A1
(ii) \(t = 10 \Rightarrow v = – 100{\text{ (m}}{{\text{s}}^{ – 1}}{\text{)}}\) A1
(iii) \(s = \int { – 10t{\text{d}}t = – 5{t^2}( + c)} \) M1A1
\(s = 1000{\text{ for }}t = 0 \Rightarrow c = 1000\) (M1)
\(s = – 5{t^2} + 1000\) A1
at \(t = 10,{\text{ }}s = 500{\text{ (m)}}\) AG
Note: Accept use of definite integrals.
[6 marks]
\(\frac{{{\text{d}}t}}{{{\text{d}}v}} = \frac{1}{{( – 10 – 5v)}}\) A1
[1 mark]
METHOD 1
\(t = \int {\frac{1}{{ – 10 – 5v}}{\text{d}}v = – \frac{1}{5}\ln ( – 10 – 5v)( + c)} \) M1A1
Note: Accept equivalent forms using modulus signs.
\(t = 10,{\text{ }}v = – 100\)
\(10 = – \frac{1}{5}\ln (490) + c\) M1
\(c = 10 + \frac{1}{5}\ln (490)\) A1
\(t = 10 + \frac{1}{5}\ln 490 – \frac{1}{5}\ln ( – 10 – 5v)\) A1
Note: Accept equivalent forms using modulus signs.
\(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\) AG
Note: Accept use of definite integrals.
METHOD 2
\(t = \int {\frac{1}{{ – 10 – 5v}}{\text{d}}v = – \frac{1}{5}\int {\frac{1}{{2 + v}}{\text{d}}v = – \frac{1}{5}\ln \left| {2 + v} \right|( + c)} } \) M1A1
Note: Accept equivalent forms.
\(t = 10,{\text{ }}v = – 100\)
\(10 = – \frac{1}{5}\ln \left| { – 98} \right| + c\) M1
Note: If \(\ln ( – 98)\) is seen do not award further A marks.
\(c = 10 + \frac{1}{5}\ln 98\) A1
\(t = 10 + \frac{1}{5}\ln 98 – \frac{1}{5}\ln \left| {2 + v} \right|\) A1
Note: Accept equivalent forms.
\(t = 10 + \frac{1}{5}\ln \left( {\frac{{98}}{{ – 2 – v}}} \right)\) AG
Note: Accept use of definite integrals.
[5 marks]
\(5(t – 10) = \ln \frac{{98}}{{( – 2 – v)}}\)
\(\frac{{2 + v}}{{98}} = – {{\text{e}}^{ – 5(t – 10)}}\) (M1)
\(v = – 2 – 98{{\text{e}}^{ – 5(t – 10)}}\) A1
[2 marks]
\(\frac{{{\text{d}}s}}{{{\text{d}}t}} = – 2 – 98{{\text{e}}^{ – 5(t – 10)}}\)
\(s = – 2t + \frac{{98}}{5}{{\text{e}}^{ – 5(t – 10)}}( + k)\) M1A1
at \(t = 10,{\text{ }}s = 500 \Rightarrow 500 = – 20 + \frac{{98}}{5} + k \Rightarrow k = 500.4\) M1A1
\(s = – 2t + \frac{{98}}{5}{{\text{e}}^{ – 5(t – 10)}} + 500.4\) A1
Note: Accept use of definite integrals.
[5 marks]
\(t = 250{\text{ for }}s = 0\) (M1)A1
[2 marks]
Total [21 marks]
Examiners report
Parts (i) and (ii) were well answered by most candidates.
In (iii) the constant of integration was often forgotten. Most candidates calculated the displacement and then used different strategies, mostly incorrect, to remove the negative sign from \( – 500\).
Surprisingly part (b) was not well done as the question stated the method. Many candidates simply wrote down \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\) while others seemed unaware that \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\) was the acceleration.
Part (c) was not always well done as it followed from (b) and at times there was very little to allow follow through. Once again some candidates started with what they were trying to prove. Among the candidates that attempted to integrate many did not consider the constant of integration properly.
In part (d) many candidates ignored the answer given in (c) and attempted to manipulate different expressions.
Part (e) was poorly answered: the constant of integration was often again forgotten and some inappropriate uses of Physics formulas assuming that the acceleration was constant were used. There was unclear thinking with the two sides of an equation being integrated with respect to different variables.
Although part (e) was often incorrect, some follow through marks were gained in part (f).
Question
A particle moves in a straight line, its velocity \(v{\text{ m}}{{\text{s}}^{ – 1}}\) at time \(t\) seconds is given by \(v = 9t – 3{t^2},{\text{ }}0 \le t \le 5\).
At time \(t = 0\), the displacement \(s\) of the particle from an origin \(O\) is 3 m.
Find the displacement of the particle when \(t = 4\).
Sketch a displacement/time graph for the particle, \(0 \le t \le 5\), showing clearly where the curve meets the axes and the coordinates of the points where the displacement takes greatest and least values.
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Given further that \(s = 16.5\) when \(t = 7.5\), find the values of \(a\) and \(b\).
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Find the times \({t_1}\) and \({t_2}(0 < {t_1} < {t_2} < 8)\) when the particle returns to its starting point.
Answer/Explanation
Markscheme
METHOD 1
\(s = \int {(9t – 3{t^2}){\text{d}}t = \frac{9}{2}{t^2} – {t^3}( + c)} \) (M1)
\(t = 0,{\text{ }}s = 3 \Rightarrow c = 3\) (A1)
\(t = 4 \Rightarrow s = 11\) A1
METHOD 2
\(s = 3 + \int_0^4 {(9t – 3{t^2}){\text{d}}t} \) (M1)(A1)
\(s = 11\) A1
[3 marks]
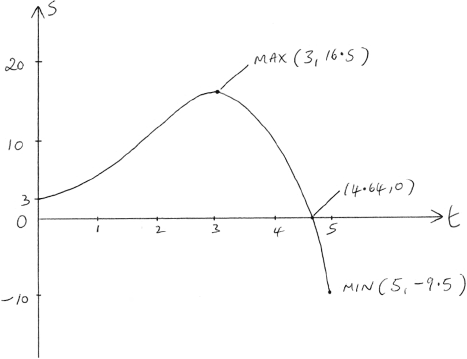
correct shape over correct domain A1
maximum at \((3,{\text{ }}16.5)\) A1
\(t\) intercept at \(4.64\), \(s\) intercept at \(3\) A1
minimum at \((5,{\text{ }} – 9.5)\) A1
[5 marks]
\( – 9.5 = a + b\cos 2\pi \)
\(16.5 = a + b\cos 3\pi \) (M1)
Note: Only award M1 if two simultaneous equations are formed over the correct domain.
\(a = \frac{7}{2}\) A1
\(b = – 13\) A1
[3 marks]
at \({t_1}\):
\(3 + \frac{9}{2}{t^2} – {t^3} = 3\) (M1)
\({t^2}\left( {\frac{9}{2} – t} \right) = 0\)
\({t_1} = \frac{9}{2}\) A1
solving \(\frac{7}{2} – 13\cos \frac{{2\pi t}}{5} = 3\) (M1)
\({\text{GDC}} \Rightarrow {t_2} = 6.22\) A1
Note: Accept graphical approaches.
[4 marks]
Total [15 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
A particle can move along a straight line from a point \(O\). The velocity \(v\), in \({\text{m}}{{\text{s}}^{ – 1}}\), is given by the function \(v(t) = 1 – {{\text{e}}^{ – \sin {t^2}}}\) where time \(t \ge 0\) is measured in seconds.
Write down the first two times \({t_1},{\text{ }}{t_2} > 0\), when the particle changes direction.
(i) Find the time \(t < {t_2}\) when the particle has a maximum velocity.
(ii) Find the time \(t < {t_2}\) when the particle has a minimum velocity.
Find the distance travelled by the particle between times \(t = {t_1}\) and \(t = {t_2}\).
Answer/Explanation
Markscheme
\({t_1} = 1.77{\text{ (s)}}\;\;\;\left( { = \sqrt \pi {\text{ (s)}}} \right)\;\;\;{\text{and}}\;\;\;{t_2} = 2.51{\text{ (s)}}\;\;\;\left( { = \sqrt {2\pi } {\text{ (s)}}} \right)\) A1A1
[2 marks]
(i) attempting to find (graphically or analytically) the first \({t_{\max }}\) (M1)
\(t = 1.25{\text{ (s)}}\;\;\;\left( { = \sqrt {\frac{\pi }{2}} {\text{ (s)}}} \right)\) A1
(ii) attempting to find (graphically or analytically) the first \({t_{\min }}\) (M1)
\(t = 2.17{\text{ (s)}}\;\;\;\left( { = \sqrt {\frac{{3\pi }}{2}} {\text{ (s)}}} \right)\) A1
[4 marks]
distance travelled \( = \left| {\int_{1.772 \ldots }^{2.506 \ldots } {1 – {{\text{e}}^{ – \sin {t^2}}}{\text{d}}t} } \right|\;\;\;\)(or equivalent) (M1)
\( = 0.711{\text{ (m)}}\) A1
Note: Award M1 for attempting to form a definite integral involving \(1 – {{\text{e}}^{ – \sin {t^2}}}\). To award the A1, correct limits leading to \(0.711\) must include the use of absolute value or a statement such as “distance must be positive”.
In part (c), award A1FT for a candidate working in degree mode \(\left( {5.39{\text{ (m)}}} \right)\).
[2 marks]
Total [8 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The displacement, \(s\), in metres, of a particle \(t\) seconds after it passes through the origin is given by the expression \(s = \ln (2 – {e^{ – t}}),{\text{ }}t \geqslant 0\).
Find an expression for the velocity, \(v\), of the particle at time \(t\).
Find an expression for the acceleration, \(a\), of the particle at time \(t\).
Find the acceleration of the particle at time \(t = 0\).
Answer/Explanation
Markscheme
\(v – \frac{{{\text{d}}s}}{{{\text{d}}t}} = \frac{{{{\text{e}}^{ – t}}}}{{2 – {{\text{e}}^{ – t}}}}{\text{ }}\left( { = \frac{1}{{2{{\text{e}}^t} – 1}}{\text{ or }} – 1 + \frac{2}{{2 – {{\text{e}}^{ – t}}}}} \right)\) M1A1
[2 marks]
\(a = \frac{{{{\text{d}}^2}s}}{{{\text{d}}{t^2}}} = \frac{{ – {{\text{e}}^{ – t}}(2 – {{\text{e}}^{ – t}}{\text{)}} – {{\text{e}}^{ – t}} \times {{\text{e}}^{ – t}}}}{{{{(2 – {{\text{e}}^{ – t}})}^2}}}{\text{ }}\left( { = \frac{{ – 2{{\text{e}}^{ – t}}}}{{{{(2 – {{\text{e}}^{ – t}})}^2}}}} \right)\) M1A1
Note: If simplified in part (a) award (M1)A1 for \(a = \frac{{{{\text{d}}^2}s}}{{{\text{d}}{t^2}}} = \frac{{ – 2{{\text{e}}^t}}}{{{{(2{{\text{e}}^t} – 1)}^2}}}\).
Note: Award M1A1 for \(a = – {{\text{e}}^{ – t}}{(2 – {{\text{e}}^{ – t}})^{ – 2}}({{\text{e}}^{ – t}}) – {{\text{e}}^{ – t}}{(2 – {{\text{e}}^{ – t}})^{ – 1}}\).
[2 marks]
\(a = – 2{\text{ }}({\text{m}}{{\text{s}}^{ – 2}})\) A1
[1 mark]
Examiners report
Mostly well done. There were a few sign errors but most candidates were correctly applying the quotient or chain rules.
Mostly well done. There were a few sign errors but most candidates were correctly applying the quotient or chain rules.
Mostly well done. There were a few sign errors but most candidates were correctly applying the quotient or chain rules.
Question
A particle moves such that its velocity \(v\,{\text{m}}{{\text{s}}^{ – 1}}\) is related to its displacement \(s\,{\text{m}}\), by the equation \(v(s) = \arctan (\sin s),{\text{ }}0 \leqslant s \leqslant 1\). The particle’s acceleration is \(a\,{\text{m}}{{\text{s}}^{ – 2}}\).
Find the particle’s acceleration in terms of \(s\).
Using an appropriate sketch graph, find the particle’s displacement when its acceleration is \(0.25{\text{ m}}{{\text{s}}^{ – 2}}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{{\cos s}}{{{{\sin }^2}s + 1}}\) M1A1
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\) (M1)
\(a = \frac{{\arctan (\sin s)\cos s}}{{{{\sin }^2}s + 1}}\) A1
[4 marks]
EITHER
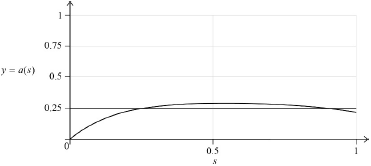(M1)
OR
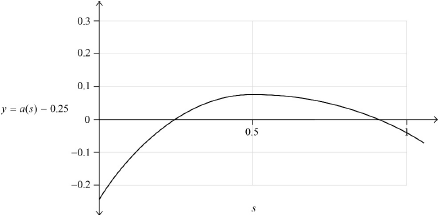(M1)
THEN
\(s = 0.296,{\text{ }}0.918{\text{ (m)}}\) A1
[2 marks]
Examiners report
In part (a), a large number of candidates thought that \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}v}}{{{\text{d}}s}}\) rather than \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}s}}{{{\text{d}}t}} \times \frac{{{\text{d}}v}}{{{\text{d}}s}} = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\).
In part (b), quite a few of these candidates then went on to find a value of \(s\) that was outside the domain \(0 \leqslant s \leqslant 1\).
Question
A point P moves in a straight line with velocity \(v\) ms−1 given by \(v\left( t \right) = {{\text{e}}^{ – t}} – 8{t^2}{{\text{e}}^{ – 2t}}\) at time t seconds, where t ≥ 0.
Determine the first time t1 at which P has zero velocity.
Find an expression for the acceleration of P at time t.
Find the value of the acceleration of P at time t1.
Answer/Explanation
Markscheme
attempt to solve \(v\left( t \right) = 0\) for t or equivalent (M1)
t1 = 0.441(s) A1
[2 marks]
\(a\left( t \right) = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – {{\text{e}}^{ – t}} – 16t{{\text{e}}^{ – 2t}} + 16{t^2}{{\text{e}}^{ – 2t}}\) M1A1
Note: Award M1 for attempting to differentiate using the product rule.
[2 marks]
\(a\left( {{t_1}} \right) = – 2.28\) (ms−2) A1
[1 mark]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The particle P moves along the x-axis such that its velocity, \(v{\text{ m}}{{\text{s}}^{ – 1}}\) , at time t seconds is given by \(v = \cos ({t^2})\).
Given that P is at the origin O at time t = 0 , calculate
(i) the displacement of P from O after 3 seconds;
(ii) the total distance travelled by P in the first 3 seconds.
Find the time at which the total distance travelled by P is 1 m.
Answer/Explanation
Markscheme
(i) displacement \( = \int_0^3 {v{\text{d}}t} \) (M1)
\( = 0.703{\text{ (m)}}\) A1
(ii) total distance \({\text{ = }}\int_0^3 {\left| v \right|{\text{d}}t} \) (M1)
\( = 2.05{\text{ (m)}}\) A1
[4 marks]
solving the equation \(\int_0^t {\left| {\cos ({u^2})} \right|{\text{d}}u = 1} \) (M1)
\(t = 1.39{\text{ (s)}}\) A1
[2 marks]
Examiners report
[N/A]
[N/A]