Download IITian Academy App for accessing Online Mock Tests and More..
Question
A particle moves in a straight line with velocity v metres per second. At any time t seconds, \(0 \leqslant t < \frac{{3\pi }}{4}\), the velocity is given by the differential equation \(\frac{{{\text{d}}v}}{{{\text{d}}t}} + {v^2} + 1 = 0\) .
It is also given that v = 1 when t = 0 .
Find an expression for v in terms of t .
Sketch the graph of v against t , clearly showing the coordinates of any intercepts, and the equations of any asymptotes.
(i) Write down the time T at which the velocity is zero.
(ii) Find the distance travelled in the interval [0, T] .
Find an expression for s , the displacement, in terms of t , given that s = 0 when t = 0 .
Hence, or otherwise, show that \(s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = – {v^2} – 1\)
attempt to separate the variables M1
\(\int {\frac{1}{{1 + {v^2}}}{\text{d}}v = \int { – 1{\text{d}}t} } \) A1
\(\arctan v = – t + k\) A1A1
Note: Do not penalize the lack of constant at this stage.
when t = 0, v = 1 M1
\( \Rightarrow k = \arctan 1 = \left( {\frac{\pi }{4}} \right) = (45^\circ )\) A1
\( \Rightarrow v = \tan \left( {\frac{\pi }{4} – t} \right)\) A1
[7 marks]
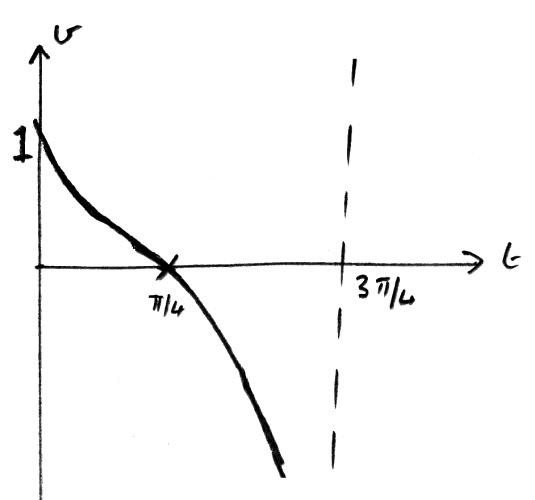A1A1A1
Note: Award A1 for general shape,
A1 for asymptote,
A1 for correct t and v intercept.
Note: Do not penalise if a larger domain is used.
[3 marks]
(i) \(T = \frac{\pi }{4}\) A1
(ii) area under curve \( = \int_0^{\frac{\pi }{4}} {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) (M1)
\( = 0.347\left( { = \frac{1}{2}\ln 2} \right)\) A1
[3 marks]
\(v = \tan \left( {\frac{\pi }{4} – t} \right)\)
\(s = \int {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) M1
\(\int {\frac{{\sin \left( {\frac{\pi }{4} – t} \right)}}{{\cos \left( {\frac{\pi }{4} – t} \right)}}} {\text{ d}}t\) (M1)
\( = \ln \cos \left( {\frac{\pi }{4} – t} \right) + k\) A1
when \(t = 0,{\text{ }}s = 0\)
\(k = – \ln \cos \frac{\pi }{4}\) A1
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\left( { = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – t} \right)} \right]} \right)\) A1
[5 marks]
METHOD 1
\(\frac{\pi }{4} – t = \arctan v\) M1
\(t = \frac{\pi }{4} – \arctan v\)
\(s = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – \frac{\pi }{4} + \arctan v} \right)} \right]\)
\(s = \ln \left[ {\sqrt 2 \cos (\arctan v)} \right]\) M1A1
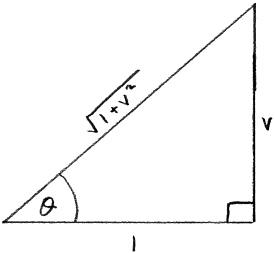
\(s = \ln \left[ {\sqrt 2 \cos \left( {\arccos \frac{1}{{\sqrt {1 + {v^2}} }}} \right)} \right]\) A1
\( = \ln \frac{{\sqrt 2 }}{{\sqrt {1 + {v^2}} }}\)
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 2
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\)
\( = – \ln \sec \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {{\tan }^2}\left( {\frac{\pi }{4} – t} \right)} – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {v^2}} – \ln \cos \frac{\pi }{4}\) A1
\( = \ln \frac{1}{{\sqrt {1 + {v^2}} }} + \ln \sqrt 2 \) A1
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 3
\(v\frac{{dv}}{{ds}} = – {v^2} – 1\) M1
\(\int {\frac{v}{{{v^2} + 1}}dv = – \int {1ds} } \) M1
\(\frac{1}{2}\ln ({v^2} + 1) = – s + k\) A1
when \(s = 0\,,{\text{ }}t = 0 \Rightarrow v = 1\)
\( \Rightarrow k = \frac{1}{2}\ln 2\) A1
\( \Rightarrow s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
[4 marks]
Examiners report
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
Question
A particle moves in a straight line with velocity v metres per second. At any time t seconds, \(0 \leqslant t < \frac{{3\pi }}{4}\), the velocity is given by the differential equation \(\frac{{{\text{d}}v}}{{{\text{d}}t}} + {v^2} + 1 = 0\) .
It is also given that v = 1 when t = 0 .
Find an expression for v in terms of t .
Sketch the graph of v against t , clearly showing the coordinates of any intercepts, and the equations of any asymptotes.
(i) Write down the time T at which the velocity is zero.
(ii) Find the distance travelled in the interval [0, T] .
Find an expression for s , the displacement, in terms of t , given that s = 0 when t = 0 .
Hence, or otherwise, show that \(s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = – {v^2} – 1\)
attempt to separate the variables M1
\(\int {\frac{1}{{1 + {v^2}}}{\text{d}}v = \int { – 1{\text{d}}t} } \) A1
\(\arctan v = – t + k\) A1A1
Note: Do not penalize the lack of constant at this stage.
when t = 0, v = 1 M1
\( \Rightarrow k = \arctan 1 = \left( {\frac{\pi }{4}} \right) = (45^\circ )\) A1
\( \Rightarrow v = \tan \left( {\frac{\pi }{4} – t} \right)\) A1
[7 marks]
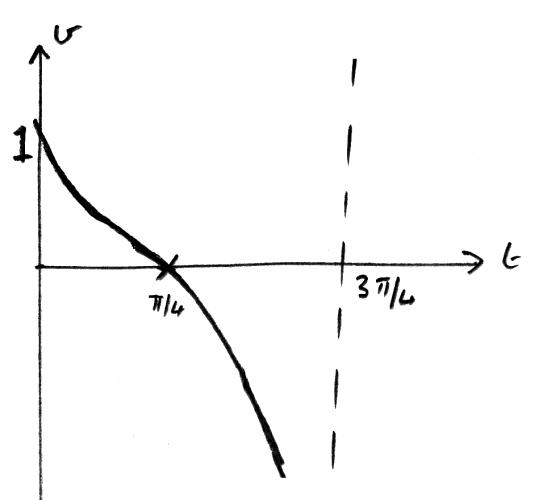A1A1A1
Note: Award A1 for general shape,
A1 for asymptote,
A1 for correct t and v intercept.
Note: Do not penalise if a larger domain is used.
[3 marks]
(i) \(T = \frac{\pi }{4}\) A1
(ii) area under curve \( = \int_0^{\frac{\pi }{4}} {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) (M1)
\( = 0.347\left( { = \frac{1}{2}\ln 2} \right)\) A1
[3 marks]
\(v = \tan \left( {\frac{\pi }{4} – t} \right)\)
\(s = \int {\tan \left( {\frac{\pi }{4} – t} \right){\text{d}}t} \) M1
\(\int {\frac{{\sin \left( {\frac{\pi }{4} – t} \right)}}{{\cos \left( {\frac{\pi }{4} – t} \right)}}} {\text{ d}}t\) (M1)
\( = \ln \cos \left( {\frac{\pi }{4} – t} \right) + k\) A1
when \(t = 0,{\text{ }}s = 0\)
\(k = – \ln \cos \frac{\pi }{4}\) A1
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\left( { = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – t} \right)} \right]} \right)\) A1
[5 marks]
METHOD 1
\(\frac{\pi }{4} – t = \arctan v\) M1
\(t = \frac{\pi }{4} – \arctan v\)
\(s = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} – \frac{\pi }{4} + \arctan v} \right)} \right]\)
\(s = \ln \left[ {\sqrt 2 \cos (\arctan v)} \right]\) M1A1
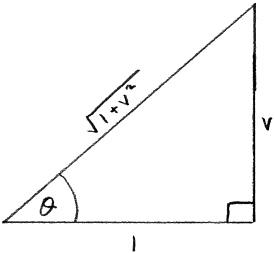
\(s = \ln \left[ {\sqrt 2 \cos \left( {\arccos \frac{1}{{\sqrt {1 + {v^2}} }}} \right)} \right]\) A1
\( = \ln \frac{{\sqrt 2 }}{{\sqrt {1 + {v^2}} }}\)
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 2
\(s = \ln \cos \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\)
\( = – \ln \sec \left( {\frac{\pi }{4} – t} \right) – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {{\tan }^2}\left( {\frac{\pi }{4} – t} \right)} – \ln \cos \frac{\pi }{4}\) M1
\( = – \ln \sqrt {1 + {v^2}} – \ln \cos \frac{\pi }{4}\) A1
\( = \ln \frac{1}{{\sqrt {1 + {v^2}} }} + \ln \sqrt 2 \) A1
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 3
\(v\frac{{dv}}{{ds}} = – {v^2} – 1\) M1
\(\int {\frac{v}{{{v^2} + 1}}dv = – \int {1ds} } \) M1
\(\frac{1}{2}\ln ({v^2} + 1) = – s + k\) A1
when \(s = 0\,,{\text{ }}t = 0 \Rightarrow v = 1\)
\( \Rightarrow k = \frac{1}{2}\ln 2\) A1
\( \Rightarrow s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
[4 marks]
Examiners report
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
Question
A particle can move along a straight line from a point \(O\). The velocity \(v\), in \({\text{m}}{{\text{s}}^{ – 1}}\), is given by the function \(v(t) = 1 – {{\text{e}}^{ – \sin {t^2}}}\) where time \(t \ge 0\) is measured in seconds.
Write down the first two times \({t_1},{\text{ }}{t_2} > 0\), when the particle changes direction.
(i) Find the time \(t < {t_2}\) when the particle has a maximum velocity.
(ii) Find the time \(t < {t_2}\) when the particle has a minimum velocity.
Find the distance travelled by the particle between times \(t = {t_1}\) and \(t = {t_2}\).
Answer/Explanation
Markscheme
\({t_1} = 1.77{\text{ (s)}}\;\;\;\left( { = \sqrt \pi {\text{ (s)}}} \right)\;\;\;{\text{and}}\;\;\;{t_2} = 2.51{\text{ (s)}}\;\;\;\left( { = \sqrt {2\pi } {\text{ (s)}}} \right)\) A1A1
[2 marks]
(i) attempting to find (graphically or analytically) the first \({t_{\max }}\) (M1)
\(t = 1.25{\text{ (s)}}\;\;\;\left( { = \sqrt {\frac{\pi }{2}} {\text{ (s)}}} \right)\) A1
(ii) attempting to find (graphically or analytically) the first \({t_{\min }}\) (M1)
\(t = 2.17{\text{ (s)}}\;\;\;\left( { = \sqrt {\frac{{3\pi }}{2}} {\text{ (s)}}} \right)\) A1
[4 marks]
distance travelled \( = \left| {\int_{1.772 \ldots }^{2.506 \ldots } {1 – {{\text{e}}^{ – \sin {t^2}}}{\text{d}}t} } \right|\;\;\;\)(or equivalent) (M1)
\( = 0.711{\text{ (m)}}\) A1
Note: Award M1 for attempting to form a definite integral involving \(1 – {{\text{e}}^{ – \sin {t^2}}}\). To award the A1, correct limits leading to \(0.711\) must include the use of absolute value or a statement such as “distance must be positive”.
In part (c), award A1FT for a candidate working in degree mode \(\left( {5.39{\text{ (m)}}} \right)\).
[2 marks]
Total [8 marks]
Examiners report
[N/A]
[N/A]
[N/A]