Question
The universal set contains all the positive integers less than 30. The set A contains all prime numbers less than 30 and the set B contains all positive integers of the form \(3 + 5n{\text{ }}(n \in \mathbb{N})\) that are less than 30. Determine the elements of
a.A \ B ;[4]
b.\(A\Delta B\) .[3]
▶️Answer/Explanation
Markscheme
A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29} (A1)
B = {3, 8, 13, 18, 23, 28} (A1)
Note: FT on their A and B
A \ B = {elements in A that are not in B} (M1)
= {2, 5, 7, 11, 17, 19, 29} A1
[4 marks]
\(B\backslash A\) = {8, 18, 28} (A1)
\(A\Delta B = (A\backslash B) \cup (B\backslash A)\) (M1)
= {2, 5, 7, 8, 11, 17, 18, 19, 28, 29} A1
[3 marks]
Examiners report
It was disappointing to find that many candidates wrote the elements of A and B incorrectly. The most common errors were the inclusion of 1 as a prime number and the exclusion of 3 in B. It has been suggested that some candidates use N to denote the positive integers. If this is the case, then it is important to emphasise that the IB notation is that N denotes the positive integers and zero and IB candidates should all be aware of that. Most candidates solved the remaining parts of the question correctly and follow through ensured that those candidates with incorrect A and/or B were not penalised any further.
It was disappointing to find that many candidates wrote the elements of A and B incorrectly. The most common errors were the inclusion of 1 as a prime number and the exclusion of 3 in B. It has been suggested that some candidates use N to denote the positive integers. If this is the case, then it is important to emphasise that the IB notation is that N denotes the positive integers and zero and IB candidates should all be aware of that. Most candidates solved the remaining parts of the question correctly and follow through ensured that those candidates with incorrect A and/or B were not penalised any further.
Question
Determine, using Venn diagrams, whether the following statements are true.
a.(i) \(A’ \cup B’ = (A \cup B)’\)
(ii) \((A\backslash B) \cup (B\backslash A) = (A \cup B)\backslash (A \cap B)\)[6]
b.Prove, without using a Venn diagram, that \(A\backslash B\) and \(B\backslash A\) are disjoint sets.[4]
▶️Answer/Explanation
Markscheme
(a) (i)
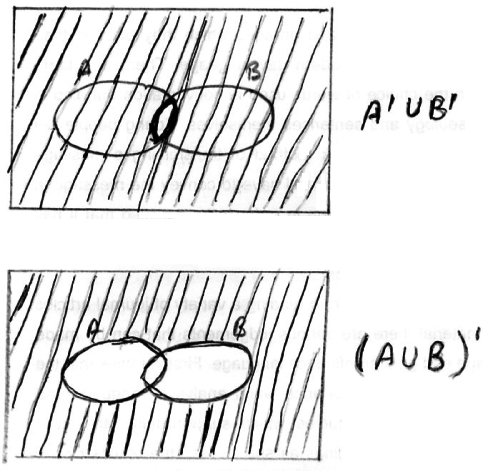 A1 A1
A1 A1
since the shaded regions are different, \(A’ \cup B’ \ne (A \cup B)’\) R1
\( \Rightarrow \) not true
(ii)
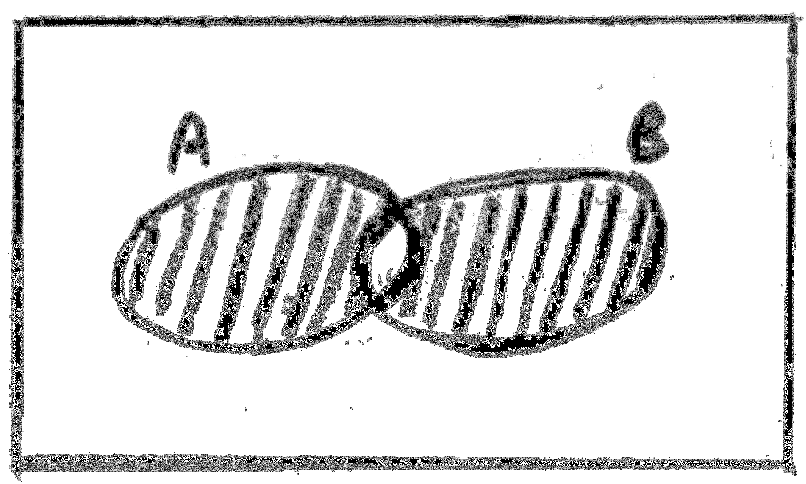 A1
A1
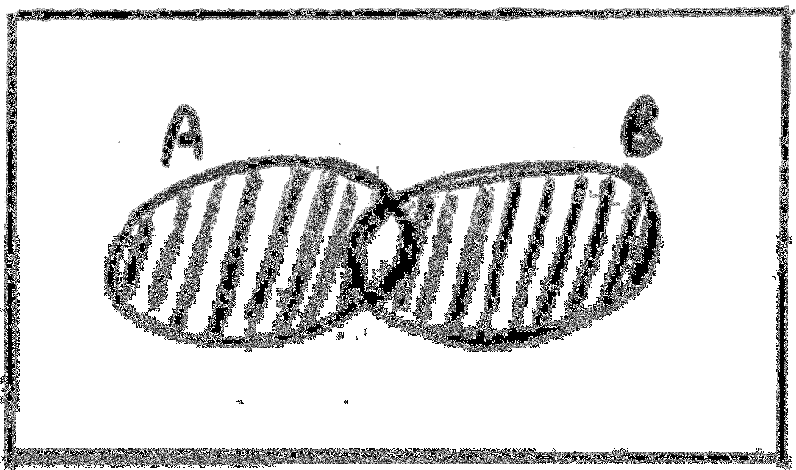 A1
A1
since the shaded regions are the same \((A\backslash B) \cup (B\backslash A) = (A \cup B)\backslash (A \cap B)\) R1
\( \Rightarrow \) true
[6 marks]
\(A\backslash B = A \cup B’\) and \(B\backslash A = B \cap A’\) (A1)
consider \(A \cap B’ \cap B \cap A’\) M1
now \(A \cap B’ \cap B \cap A’ = \emptyset \) A1
since this is the empty set, they are disjoint R1
Note: Accept alternative valid proofs.
[4 marks]
Examiners report
Part (a) was accessible to most candidates, but a number drew incorrect Venn diagrams. In some cases the clarity of the diagram made it difficult to follow what the candidate intended. Candidates found (b) harder, although the majority made a reasonable start to the proof. Once again a number of candidates were let down by poor explanation.
Part (a) was accessible to most candidates, but a number drew incorrect Venn diagrams. In some cases the clarity of the diagram made it difficult to follow what the candidate intended. Candidates found (b) harder, although the majority made a reasonable start to the proof. Once again a number of candidates were let down by poor explanation.
Question
The elements of sets P and Q are taken from the universal set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. P = {1, 2, 3} and Q = {2, 4, 6, 8, 10}.
a.Given that \(R = (P \cap Q’)’\) , list the elements of R .[3]
b.For a set S , let \({S^ * }\) denote the set of all subsets of S ,
(i) find \({P^ * }\) ;
(ii) find \(n({R^ * })\) .[5]
▶️Answer/Explanation
Markscheme
\(P = \{ 1,{\text{ }}2,{\text{ }}3\} \)
\(Q’ = \{ 1,{\text{ }}3,{\text{ }}5,{\text{ }}7,{\text{ }}9\} \)
so \(P \cap Q’ = \{ 1,{\text{ }}3\} \) (M1)(A1)
so \((P \cap Q’)’ = \{ 2,{\text{ }}4,{\text{ }}5,{\text{ }}6,{\text{ }}7,{\text{ }}8,{\text{ }}9,{\text{ }}10\} \) A1
[3 marks]
(i) \({P^ * } = \left\{ {\{ 1\} ,{\text{ }}\{ 2\} ,{\text{ }}\{ 3\} ,{\text{ }}\{ 1,{\text{ }}2\} ,{\text{ }}\{ 2,{\text{ }}3\} ,{\text{ }}\{ 3,{\text{ }}1\} ,{\text{ }}\{ 1,{\text{ }}2,{\text{ }}3),{\text{ }}\emptyset } \right\}\) A2
Note: Award A1 if one error, A0 for two or more.
(ii) \({R^ * }\) contains: the empty set (1 element); sets containing one element (8 elements); sets containing two elements (M1)
\( = \left( {\begin{array}{*{20}{c}}
8 \\
0
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
8 \\
1
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
8 \\
2
\end{array}} \right) + …\left( {\begin{array}{*{20}{c}}
8 \\
8
\end{array}} \right)\) (A1)
\( = {2^8}{\text{ }}( = 256)\) A1
Note: FT in (ii) applies if no empty set included in (i) and (ii).
[5 marks]
Examiners report
This was also a well answered question with many candidates obtaining full marks on both parts of the problem. Some candidates attempted to use a factorial rather than a sum of combinations to solve part (b) (ii) and this led to incorrect answers.
This was also a well answered question with many candidates obtaining full marks on both parts of the problem. Some candidates attempted to use a factorial rather than a sum of combinations to solve part (b) (ii) and this led to incorrect answers.
Question
(a) Given a set \(U\), and two of its subsets \(A\) and \(B\), prove that
\[(A\backslash B) \cup (B\backslash A) = (A \cup B)\backslash (A \cap B),{\text{ where }}A\backslash B = A \cap B’.\]
(b) Let \(S = \{ A,{\text{ }}B,{\text{ }}C,{\text{ }}D\} \) where \(A = \emptyset ,{\text{ }}B = \{ 0\} ,{\text{ }}C = \{ 0,{\text{ }}1\} \) and \(D = \{ {\text{0, 1, 2}}\} \).
State, with reasons, whether or not each of the following statements is true.
(i) The operation \ is closed in \(S\).
(ii) The operation \( \cap \) has an identity element in \(S\) but not all elements have an inverse.
(iii) Given \(Y \in S\), the equation \(X \cup Y = Y\) always has a unique solution for \(X\) in \(S\).
▶️Answer/Explanation
Markscheme
(a) \((A\backslash B) \cup (B\backslash A) = (A \cap B’) \cup (B \cap A’)\) (M1)
\( = \left( {(A \cap B’) \cup B} \right) \cap \left( {(A \cap B’) \cup A’} \right)\) M1
\( = \left( {(A \cup B) \cap \underbrace {(B’ \cup B)}_U} \right) \cap \left( {\underbrace {(A \cup A’)}_U \cap (B’ \cup A’)} \right)\) A1
\( = (A \cup B’) \cap (B’ \cup A’) = (A \cup B) \cap (A \cap B)’\) A1
\( = (A \cup B)\backslash (A \cap B)\) AG
[4 marks]
(b) (i) false A1
counterexample
eg \(D\backslash C = \{ 2\} \notin S\) R1
(ii) true A1
as \(A \cap D = A,{\text{ }}B \cap D = B,{\text{ }}C \cap D = C\) and \(D \cap D = D\),
\(D\) is the identity R1
\(A\) (or \(B\) or \(C\)) has no inverse as \(A \cap X = D\) is impossible R1
(iii) false A1
when \(Y = D\) the equation has more than one solution (four solutions) R1
[7 marks]
Examiners report
For part (a), candidates who chose to prove the given statement using the properties of Sets were often successful with the proof. Some candidates chose to use the definition of equality of sets, but made little to no progress. In a few cases candidates attempted to use Venn diagrams as a proof. Part (b) was challenging for most candidates, and few correct answers were seen.
