Question
a.Sets X and Y are defined by \({\text{ }}X = \left] {0,{\text{ }}1} \right[;{\text{ }}Y = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\} \).
(i) Sketch the set \(X \times Y\) in the Cartesian plane.
(ii) Sketch the set \(Y \times X\) in the Cartesian plane.
(iii) State \((X \times Y) \cap (Y \times X)\).[5]
b.Consider the function \(f:X \times Y \to \mathbb{R}\) defined by \(f(x,{\text{ }}y) = x + y\) and the function \(g:X \times Y \to \mathbb{R}\) defined by \(g(x,{\text{ }}y) = xy\).
(i) Find the range of the function f.
(ii) Find the range of the function g.
(iii) Show that \(f\) is an injection.
(iv) Find \({f^{ – 1}}(\pi )\), expressing your answer in exact form.
(v) Find all solutions to \(g(x,{\text{ }}y) = \frac{1}{2}\).[10]
▶️Answer/Explanation
Markscheme
(i) 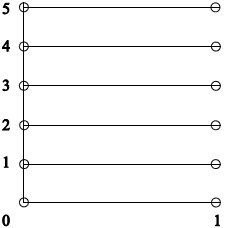
correct horizontal lines A1
correctly labelled axes A1
clear indication that the endpoints are not included A1
(ii) 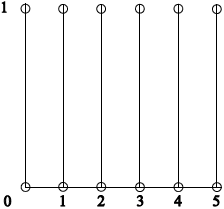
fully correct diagram A1
Note: Do not penalize the inclusion of endpoints twice.
(iii) the intersection is empty A1
[5 marks]
(i) range \((f) = \left] {0,{\text{ 1}}} \right[ \cup \left] {1,{\text{ 2}}} \right[ \cup \rm{L} \cup \left] {5,{\text{ 6}}} \right[\) A1A1
Note: A1 for six intervals and A1 for fully correct notation.
Accept \(0 < x < 6,{\text{ }}x \ne 0{\text{, 1, 2, 3, 4, 5, 6}}\).
(ii) range \((g) = \left[ {0,{\text{ 5}}} \right[\) A1
(iii) Attempt at solving
\(f({x_1},{\text{ }}{y_1}) = f({x_2},{\text{ }}{y_2})\) M1
\(f(x,{\text{ }}y) \in \left] {y,{\text{ }}y + 1} \right[ \Rightarrow {y_1} = {y_2}\) M1
and then \({x_1} = {x_2}\) A1
so \(f\) is injective AG
(iv) \({f^{ – 1}}(\pi ) = (\pi – 3,{\text{ }}3)\) A1A1
(v) solutions: (0.5, 1), (0.25, 2), \(\left( {\frac{1}{6},{\text{ 3}}} \right)\), (0.125, 4), (0.1, 5) A2
Note: A2 for all correct, A1 for 2 correct.
[10 marks]
Examiners report
[N/A]
[N/A]
Question
The relation \(R=\) is defined on \({\mathbb{Z}^ + }\) such that \(aRb\) if and only if \({b^n} – {a^n} \equiv 0(\bmod p)\) where \(n,{\text{ }}p\) are fixed positive integers greater than 1.
a.Show that \(R\) is an equivalence relation.[7]
b.Given that \(n = 2\) and \(p = 7\), determine the first four members of each of the four equivalence classes of \(R\).[5]
▶️Answer/Explanation
Markscheme
since \({a^n} – {a^n} = 0\), A1
it follows that \((aRa)\) and \(R\) is reflexive R1
if \(aRb\) so that \({b^n} – {a^n} \equiv 0(\bmod p)\) M1
then, \({a^n} – {b^n} \equiv 0(\bmod p)\) so that \(bRa\) and \(R\) is symmetric A1
if \(aRb\) and \(bRc\) so that \({b^n} – {a^n} \equiv 0(\bmod p)\) and \({c^n} – {b^n} \equiv 0(\bmod p)\) M1
adding, (it follows that \({c^n} – {a^n} \equiv 0(\bmod p)\)) M1
so that \(aRc\) and \(R\) is transitive A1
Note: Only accept the correct use of the terms “reflexive, symmetric, transitive”.
[7 marks]
we are now given that \(aRb\) if \({b^2} – {a^2} \equiv 0(\bmod 7)\)
attempt to find at least one equivalence class (M1)
the equivalence classes are
\(\{ 1,{\text{ }}6,{\text{ }}8,{\text{ }}13,{\text{ }} \ldots \} \) A1
\(\{ 2,{\text{ }}5,{\text{ }}9,{\text{ }}12,{\text{ }} \ldots \} \) A1
\(\{ 3,{\text{ }}4,{\text{ }}10,{\text{ }}11,{\text{ }} \ldots \} \) A1
\(\{ 7,{\text{ }}14,{\text{ }}21,{\text{ }}28,{\text{ }} \ldots \} \) A1
[5 marks]
Examiners report
Most candidates were familiar with the terminology of the required conditions to be satisfied for a relation to be an equivalence relation. The execution of the proofs was variable. It was grating to see such statements as \(R\) is symmetric because \(aRb = bRa\) or \(aRa = {a^n} – {a^n} = 0\), often without mention of \(\bmod p\), and such responses were not fully rewarded.
This was not well answered. Few candidates displayed a strategy to find the equivalence classes.
Question
A relation \(S\) is defined on \(\mathbb{R}\) by \(aSb\) if and only if \(ab > 0\).
A relation \(R\) is defined on a non-empty set \(A\). \(R\) is symmetric and transitive but not reflexive.
a.Show that \(S\) is
(i) not reflexive;
(ii) symmetric;
(iii) transitive.[4]
b.Explain why there exists an element \(a \in A\) that is not related to itself.[1]
c.Hence prove that there is at least one element of \(A\) that is not related to any other element of \(A\).[6]
▶️Answer/Explanation
Markscheme
(i) \(0S0\) is not true so \(S\) is not reflexive A1AG
(ii) \(aSb \Rightarrow ab > 0 \Rightarrow ba > 0 \Rightarrow bSa\) so \(S\) is symmetric R1AG
(iii) \(aSb\) and \(bSc \Rightarrow ab > 0\) and \(bc > 0 \Rightarrow a{b^2}c > 0 \Rightarrow ac > 0\) M1
since \({b^2} > 0\) (as \(b\) could not be 0) \( \Rightarrow aSc\) so \(S\) is transitive R1AG
Note: R1 is for indicating that \({b^2} > 0\).
[4 marks]
since \(R\) is not reflexive there is at least one element \(a\) belonging to \(A\) such that \(a\) is not related to \(a\) R1AG
[1 mark]
argue by contradiction: suppose that \(a\) is related to some other element \(b\), ie, \(aRb\) M1
since \(R\) is symmetric \(aRb\) implies \(bRa\) R1A1
since \(R\) is transitive \(aRb\) and \(bRa\) implies \(aRa\) R1A1
giving the required contradiction R1
hence there is at least one element of \(A\) that is not related to any other member of \(A\) AG
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The relation R is defined on \(\mathbb{R} \times \mathbb{R}\) such that \(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2})\) if and only if \({x_1}{y_1} = {x_2}{y_2}\).
a.Show that R is an equivalence relation.[5]
b.Determine the equivalence class of R containing the element \((1,{\text{ }}2)\) and illustrate this graphically.[4]
▶️Answer/Explanation
Markscheme
R is an equivalence relation if
R is reflexive, symmetric and transitive A1
\({x_1}{y_1} = {x_1}{y_1} \Rightarrow ({x_1},{\text{ }}{y_1})R({x_1},{\text{ }}{y_1})\) A1
so R is reflexive
\(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2}) \Rightarrow {x_1}{y_1} = {x_2}{y_2} \Rightarrow {x_2}{y_2} = {x_1}{y_1} \Rightarrow ({x_2},{\text{ }}{y_2})R({x_1},{\text{ }}{y_1})\) A1
so R is symmetric
\(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2})\) and \(({x_2},{\text{ }}{y_2})R({x_3},{\text{ }}{y_3}) \Rightarrow {x_1}{y_1} = {x_2}{y_2}\) and \({x_2}{y_2} = {x_3}{y_3}\) M1
\( \Rightarrow {x_1}{y_1} = {x_3}{y_3} \Rightarrow ({x_1},{\text{ }}{y_1})R({x_3},{\text{ }}{y_3})\) A1
so R is transitive
R is an equivalence relation AG
[5 marks]
\((x,{\text{ }}y)R(1,{\text{ }}2)\) (M1)
the equivalence class is \(\{ (x,{\text{ }}y)|xy = 2\} \) A1
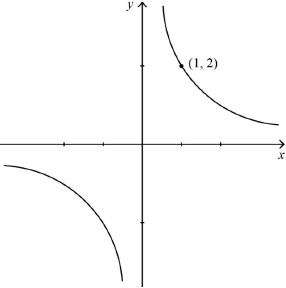
correct graph A1
\((1,{\text{ }}2)\) indicated on the graph A1
Note: Award last A1 only if plotted on a curve representing the class.
[4 marks]
Examiners report
[N/A]
[N/A]
Question
The relation \(R\) is defined such that \(xRy\) if and only if \(\left| x \right| + \left| y \right| = \left| {x + y} \right|\) for \(x\), \(y\), \(y \in \mathbb{R}\).
a.i.Show that \(R\) is reflexive.[2]
a.ii.Show that \(R\) is symmetric.[2]
b.Show, by means of an example, that \(R\) is not transitive.[4]
▶️Answer/Explanation
Markscheme
(for \(x \in \mathbb{R}\)), \(\left| x \right| + \left| x \right| = 2\left| x \right|\) A1
and \(\left| x \right| + \left| x \right| = \left| {2x} \right| = 2\left| x \right|\) A1
hence \(xRx\)
so \(R\) is reflexive AG
Note: Award A1 for correct verification of identity for \(x\) > 0; A1 for correct verification for \(x\) ≤ 0.
[2 marks]
if \(xRy \Rightarrow \left| x \right| + \left| y \right| = \left| {x + y} \right|\)
\(\left| x \right| + \left| y \right| = \left| y \right| + \left| x \right|\) A1
\(\left| {x + y} \right| = \left| {y + x} \right|\) A1
hence \(yRx\)
so \(R\) is symmetric AG
[2 marks]
recognising a condition where transitivity does not hold (M1)
(eg, \(x\) > 0, \(y\) = 0 and \(z\) < 0)
for example, 1\(R\)0 and 0\(R\)(−1) A1
however \(\left| 1 \right| + \left| { – 1} \right| \ne \left| {1 + – 1} \right|\) A1
so 1\(R\)(−1) (for example) is not true R1
hence \(R\) is not transitive AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
