Question
The group \(\{ G,{\text{ }} * \} \) is defined on the set \(G\) with binary operation \( * \). \(H\) is a subset of \(G\) defined by \(H = \{ x:{\text{ }}x \in G,{\text{ }}a * x * {a^{ – 1}} = x{\text{ for all }}a \in G\} \). Prove that \(\{ H,{\text{ }} * \} \) is a subgroup of \(\{ G,{\text{ }} * \} \).
▶️Answer/Explanation
Markscheme
associativity: This follows from associativity in \(\{ G,{\text{ }} * \} \) R1
the identity \(e \in H\) since \(a * e * {a^{ – 1}} = a * {a^{ – 1}} = e\) (for all \(a \in G\)) R1
Note: Condone the use of the commutativity of e if that is involved in an alternative simplification of the LHS.
closure: Let \(x,{\text{ }}y \in H\) so that \(a * x * {a^{ – 1}} = x\) and \(a * y * {a^{ – 1}} = y\) for all \(a \in G\) (M1)
multiplying, \(x * y = a * x * {a^{ – 1}} * a * y * {a^{ – 1}}\) (for all \(a \in G\)) A1
\( = a * x * y * {a^{ – 1}}\) A1
therefore \(x * y \in H\) (proving closure) R1
inverse: Let \(x \in H\) so that \(a * x * {a^{ – 1}} = x\) (for all \(a \in G\))
\({x^{ – 1}} = {(a * x * {a^{ – 1}})^{ – 1}}\) M1
\( = a * {x^{ – 1}} * {a^{ – 1}}\) A1
therefore \({x^{ – 1}} \in H\) R1
hence \(\{ H,{\text{ }} * \} \) is a subgroup of \(\{ G,{\text{ }} * \} \) AG
Note: Accuracy marks cannot be awarded if commutativity is assumed for general elements of \(G\).
[9 marks]
Examiners report
This is an abstract question, clearly defined on a subset. Far too many candidates almost immediately deduced, erroneously, that the full group was Abelian. Almost no marks were then available.
Question
The following Cayley table for the binary operation multiplication modulo 9, denoted by \( * \), is defined on the set \(S = \{ 1,{\text{ }}2,{\text{ }}4,{\text{ }}5,{\text{ }}7,{\text{ }}8\} \).
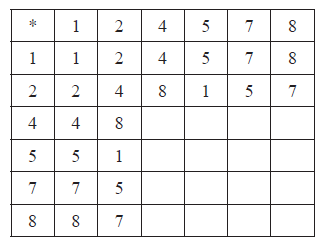
Copy and complete the table.
Show that \(\{ S,{\text{ }} * \} \) is an Abelian group.
Determine the orders of all the elements of \(\{ S,{\text{ }} * \} \).
(i) Find the two proper subgroups of \(\{ S,{\text{ }} * \} \).
(ii) Find the coset of each of these subgroups with respect to the element 5.
Solve the equation \(2 * x * 4 * x * 4 = 2\).
▶️Answer/Explanation
Markscheme
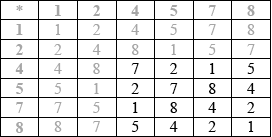 A3
A3
Note: Award A3 for correct table, A2 for one or two errors, A1 for three or four errors and A0 otherwise.
[3 marks]
the table contains only elements of \(S\), showing closure R1
the identity is 1 A1
every element has an inverse since 1 appears in every row and column, or a complete list of elements and their correct inverses A1
multiplication of numbers is associative A1
the four axioms are satisfied therefore \(\{ S,{\text{ }} * \} \) is a group
the group is Abelian because the table is symmetric (about the leading diagonal) A1
[5 marks]
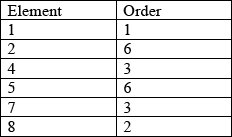 A3
A3
Note: Award A3 for all correct values, A2 for 5 correct, A1 for 4 correct and A0 otherwise.
[3 marks]
(i) the subgroups are \(\{ 1,{\text{ }}8\} \); \(\{ 1,{\text{ }}4,{\text{ }}7\} \) A1A1
(ii) the cosets are \(\{ 4,{\text{ }}5\} \); \(\{ 2,{\text{ }}5,{\text{ }}8\} \) A1A1
[4 marks]
METHOD 1
use of algebraic manipulations M1
and at least one result from the table, used correctly A1
\(x = 2\) A1
\(x = 7\) A1
METHOD 2
testing at least one value in the equation M1
obtain \(x = 2\) A1
obtain \(x = 7\) A1
explicit rejection of all other values A1
[4 marks]
Examiners report
The majority of candidates were able to complete the Cayley table correctly.
Generally well done. However, it is not good enough for a candidate to say something along the lines of ‘the operation is closed or that inverses exist by looking at the Cayley table’. A few candidates thought they only had to prove commutativity.
Often well done. A few candidates stated extra, and therefore incorrect subgroups.
[N/A]
The majority found only one solution, usually the obvious \(x = 2\), but sometimes only the less obvious \(x = 7\).
Question
The following Cayley table for the binary operation multiplication modulo 9, denoted by \( * \), is defined on the set \(S = \{ 1,{\text{ }}2,{\text{ }}4,{\text{ }}5,{\text{ }}7,{\text{ }}8\} \).
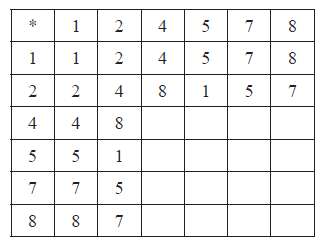
Copy and complete the table.
Show that \(\{ S,{\text{ }} * \} \) is an Abelian group.
Determine the orders of all the elements of \(\{ S,{\text{ }} * \} \).
(i) Find the two proper subgroups of \(\{ S,{\text{ }} * \} \).
(ii) Find the coset of each of these subgroups with respect to the element 5.
Solve the equation \(2 * x * 4 * x * 4 = 2\).
▶️Answer/Explanation
Markscheme
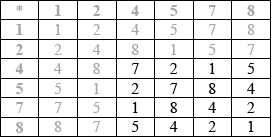 A3
A3
Note: Award A3 for correct table, A2 for one or two errors, A1 for three or four errors and A0 otherwise.
[3 marks]
the table contains only elements of \(S\), showing closure R1
the identity is 1 A1
every element has an inverse since 1 appears in every row and column, or a complete list of elements and their correct inverses A1
multiplication of numbers is associative A1
the four axioms are satisfied therefore \(\{ S,{\text{ }} * \} \) is a group
the group is Abelian because the table is symmetric (about the leading diagonal) A1
[5 marks]
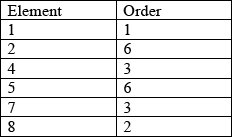 A3
A3
Note: Award A3 for all correct values, A2 for 5 correct, A1 for 4 correct and A0 otherwise.
[3 marks]
(i) the subgroups are \(\{ 1,{\text{ }}8\} \); \(\{ 1,{\text{ }}4,{\text{ }}7\} \) A1A1
(ii) the cosets are \(\{ 4,{\text{ }}5\} \); \(\{ 2,{\text{ }}5,{\text{ }}8\} \) A1A1
[4 marks]
METHOD 1
use of algebraic manipulations M1
and at least one result from the table, used correctly A1
\(x = 2\) A1
\(x = 7\) A1
METHOD 2
testing at least one value in the equation M1
obtain \(x = 2\) A1
obtain \(x = 7\) A1
explicit rejection of all other values A1
[4 marks]
Examiners report
The majority of candidates were able to complete the Cayley table correctly.
Generally well done. However, it is not good enough for a candidate to say something along the lines of ‘the operation is closed or that inverses exist by looking at the Cayley table’. A few candidates thought they only had to prove commutativity.
Often well done. A few candidates stated extra, and therefore incorrect subgroups.
[N/A]
The majority found only one solution, usually the obvious \(x = 2\), but sometimes only the less obvious \(x = 7\).
Question
\(\{ G,{\text{ }} * \} \) is a group with identity element \(e\). Let \(a,{\text{ }}b \in G\).
State Lagrange’s theorem.
Verify that the inverse of \(a * {b^{ – 1}}\) is equal to \(b * {a^{ – 1}}\).
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\). Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
Prove that \(R\) is an equivalence relation, indicating clearly whenever you are using one of the four properties required of a group.
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\) .Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
Show that \(aRb \Leftrightarrow a \in Hb\), where \(Hb\) is the right coset of \(H\) containing \(b\).
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\) .Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
It is given that the number of elements in any right coset of \(H\) is equal to the order of \(H\).
Explain how this fact together with parts (c) and (d) prove Lagrange’s theorem.
▶️Answer/Explanation
Markscheme
in a finite group the order of any subgroup (exactly) divides the order of the group A1A1
[2 marks]
METHOD 1
\((a * {b^{ – 1}}) * (b * {a^{ – 1}}) = a * {b^{ – 1}} * b * {a^{ – 1}} = a * e * {a^{ – 1}} = a * {a^{ – 1}} = e\) M1A1A1
Note: M1 for multiplying, A1 for at least one of the next 3 expressions,
A1 for \(e\).
Allow \((b * {a^{ – 1}}) * (a * {b^{ – 1}}) = b * {a^{ – 1}} * a * {b^{ – 1}} = b * e * {b^{ – 1}} = b * {b^{ – 1}} = e\).
METHOD 2
\({(a * {b^{ – 1}})^{ – 1}} = {({b^{ – 1}})^{ – 1}} * {a^{ – 1}}\) M1A1
\( = b * {a^{ – 1}}\)A1
[3 marks]
\(a * {a^{ – 1}} = e \in H\;\;\;\)(as \(H\) is a subgroup) M1
so \(aRa\) and hence \(R\) is reflexive
\(aRb \Leftrightarrow a * {b^{ – 1}} \in H\). \(H\) is a subgroup so every element has an inverse in \(H\) so
\({(a * {b^{ – 1}})^{ – 1}} \in H\) R1
\( \Leftrightarrow b * {a^{ – 1}} \in H \Leftrightarrow bRa\) M1
so \(R\) is symmetric
\(aRb,{\text{ }}bRc \Leftrightarrow a * {b^{ – 1}} \in H,{\text{ }}b * {c^{ – 1}} \in H\) M1
as \(H\) is closed \((a * {b^{ – 1}}) * {\text{(}}b * {c^{ – 1}}) \in H\) R1
and using associativity R1
\((a * {b^{ – 1}}) * {\text{(}}b * {c^{ – 1}}) = a * ({b^{ – 1}} * b) * {c^{ – 1}} = a * {c^{ – 1}} \in H \Leftrightarrow aRc\) A1
therefore \(R\) is transitive
\(R\) is reflexive, symmetric and transitive
Note: Can be said separately at the end of each part.
hence it is an equivalence relation AG
[8 marks]
\(aRb \Leftrightarrow a * {b^{ – 1}} \in H \Leftrightarrow a * {b^{ – 1}} = h \in H\) A1
\( \Leftrightarrow a = h * b \Leftrightarrow a \in Hb\) M1R1
[3 marks]
(d) implies that the right cosets of \(H\) are equal to the equivalence classes of the relation in (c) R1
hence the cosets partition \(G\) R1
all the cosets are of the same size as the subgroup \(H\) so the order of \(G\) must be a multiple of \(\left| H \right|\) R1
[3 marks]
Total [19 marks]
Examiners report
Many students obtained just half marks in (a) for not stating the requirement of the order to be finite.
Part (b) should have been more straightforward than many found.
In part (c) it was evident that most candidates knew what to do, but being a more difficult question fell down on a lack of rigour. Nonetheless, many candidates obtained full or partial marks on this question part.
Part (d) enabled many candidates to obtain, at least partial marks, but there were few students with the insight to be able to answer part (e) satisfactorily.
Part (d) enabled many candidates to obtain, at least partial marks, but there were few students with the insight to be able to answer part (e) satisfactorily.
Question
Let \(f:G \to H\) be a homomorphism of finite groups.
Prove that \(f({e_G}) = {e_H}\), where \({e_G}\) is the identity element in \(G\) and \({e_H}\) is the identity
element in \(H\).
(i) Prove that the kernel of \(f,{\text{ }}K = {\text{Ker}}(f)\), is closed under the group operation.
(ii) Deduce that \(K\) is a subgroup of \(G\).
(i) Prove that \(gk{g^{ – 1}} \in K\) for all \(g \in G,{\text{ }}k \in K\).
(ii) Deduce that each left coset of K in G is also a right coset.
▶️Answer/Explanation
Markscheme
\(f(g) = f({e_G}g) = f({e_G})f(g)\) for \(g \in G\) M1A1
\( \Rightarrow f({e_G}) = {e_H}\) AG
[2 marks]
(i) closure: let \({k_1}\) and \({k_2} \in K\), then \(f({k_1}{k_2}) = f({k_1})f({k_2})\) M1A1
\( = {e_H}{e_H} = {e_H}\) A1
hence \({k_1}{k_2} \in K\) R1
(ii) K is non-empty because \({e_G}\) belongs to K R1
a closed non-empty subset of a finite group is a subgroup R1AG
[6 marks]
(i) \(f(gk{g^{ – 1}}) = f(g)f(k)f({g^{ – 1}})\) M1
\( = f(g){e_H}f({g^{ – 1}}) = f(g{g^{ – 1}})\) A1
\( = f({e_G}) = {e_H}\) A1
\( \Rightarrow gk{g^{ – 1}} \in K\) AG
(ii) clear definition of both left and right cosets, seen somewhere. A1
use of part (i) to show \(gK \subseteq Kg\) M1
similarly \(Kg \subseteq gK\) A1
hence \(gK = Kg\) AG
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
\(\{ G,{\text{ }} * \} \) is a group with identity element \(e\). Let \(a,{\text{ }}b \in G\).
State Lagrange’s theorem.
Verify that the inverse of \(a * {b^{ – 1}}\) is equal to \(b * {a^{ – 1}}\).
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\). Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
Prove that \(R\) is an equivalence relation, indicating clearly whenever you are using one of the four properties required of a group.
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\) .Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
Show that \(aRb \Leftrightarrow a \in Hb\), where \(Hb\) is the right coset of \(H\) containing \(b\).
Let \(\{ H,{\rm{ }} * {\rm{\} }}\) be a subgroup of \(\{ G,{\rm{ }} * {\rm{\} }}\) .Let \(R\) be a relation defined on \(G\) by
\[aRb \Leftrightarrow a * {b^{ – 1}} \in H.\]
It is given that the number of elements in any right coset of \(H\) is equal to the order of \(H\).
Explain how this fact together with parts (c) and (d) prove Lagrange’s theorem.
▶️Answer/Explanation
Markscheme
in a finite group the order of any subgroup (exactly) divides the order of the group A1A1
[2 marks]
METHOD 1
\((a * {b^{ – 1}}) * (b * {a^{ – 1}}) = a * {b^{ – 1}} * b * {a^{ – 1}} = a * e * {a^{ – 1}} = a * {a^{ – 1}} = e\) M1A1A1
Note: M1 for multiplying, A1 for at least one of the next 3 expressions,
A1 for \(e\).
Allow \((b * {a^{ – 1}}) * (a * {b^{ – 1}}) = b * {a^{ – 1}} * a * {b^{ – 1}} = b * e * {b^{ – 1}} = b * {b^{ – 1}} = e\).
METHOD 2
\({(a * {b^{ – 1}})^{ – 1}} = {({b^{ – 1}})^{ – 1}} * {a^{ – 1}}\) M1A1
\( = b * {a^{ – 1}}\)A1
[3 marks]
\(a * {a^{ – 1}} = e \in H\;\;\;\)(as \(H\) is a subgroup) M1
so \(aRa\) and hence \(R\) is reflexive
\(aRb \Leftrightarrow a * {b^{ – 1}} \in H\). \(H\) is a subgroup so every element has an inverse in \(H\) so
\({(a * {b^{ – 1}})^{ – 1}} \in H\) R1
\( \Leftrightarrow b * {a^{ – 1}} \in H \Leftrightarrow bRa\) M1
so \(R\) is symmetric
\(aRb,{\text{ }}bRc \Leftrightarrow a * {b^{ – 1}} \in H,{\text{ }}b * {c^{ – 1}} \in H\) M1
as \(H\) is closed \((a * {b^{ – 1}}) * {\text{(}}b * {c^{ – 1}}) \in H\) R1
and using associativity R1
\((a * {b^{ – 1}}) * {\text{(}}b * {c^{ – 1}}) = a * ({b^{ – 1}} * b) * {c^{ – 1}} = a * {c^{ – 1}} \in H \Leftrightarrow aRc\) A1
therefore \(R\) is transitive
\(R\) is reflexive, symmetric and transitive
Note: Can be said separately at the end of each part.
hence it is an equivalence relation AG
[8 marks]
\(aRb \Leftrightarrow a * {b^{ – 1}} \in H \Leftrightarrow a * {b^{ – 1}} = h \in H\) A1
\( \Leftrightarrow a = h * b \Leftrightarrow a \in Hb\) M1R1
[3 marks]
(d) implies that the right cosets of \(H\) are equal to the equivalence classes of the relation in (c) R1
hence the cosets partition \(G\) R1
all the cosets are of the same size as the subgroup \(H\) so the order of \(G\) must be a multiple of \(\left| H \right|\) R1
[3 marks]
Total [19 marks]
Examiners report
Many students obtained just half marks in (a) for not stating the requirement of the order to be finite.
Part (b) should have been more straightforward than many found.
In part (c) it was evident that most candidates knew what to do, but being a more difficult question fell down on a lack of rigour. Nonetheless, many candidates obtained full or partial marks on this question part.
Part (d) enabled many candidates to obtain, at least partial marks, but there were few students with the insight to be able to answer part (e) satisfactorily.
Part (d) enabled many candidates to obtain, at least partial marks, but there were few students with the insight to be able to answer part (e) satisfactorily.
