Question
The binary operation \( * \) is defined by
\(a * b = a + b – 3\) for \(a,{\text{ }}b \in \mathbb{Z}\).
The binary operation \( \circ \) is defined by
\(a \circ b = a + b + 3\) for \(a,{\text{ }}b \in \mathbb{Z}\).
Consider the group \(\{ \mathbb{Z},{\text{ }} \circ {\text{\} }}\) and the bijection \(f:\mathbb{Z} \to \mathbb{Z}\) given by \(f(a) = a – 6\).
a.Show that \(\{ \mathbb{Z},{\text{ }} * \} \) is an Abelian group.[9]
b.Show that there is no element of order 2.[2]
c.Find a proper subgroup of \(\{ \mathbb{Z},{\text{ }} * \} \).[2]
d.Show that the groups \(\{ \mathbb{Z},{\text{ }} * \} \) and \(\{ \mathbb{Z},{\text{ }} \circ \} \) are isomorphic.[3]
▶️Answer/Explanation
Markscheme
closure: \(\{ \mathbb{Z},{\text{ }} * \} \) is closed because \(a + b – 3 \in \mathbb{Z}\) R1
identity: \(a * e = a + e – 3 = a\) (M1)
\(e = 3\) A1
inverse: \(a * {a^{ – 1}} = a + {a^{ – 1}} – 3 = 3\) (M1)
\({a^{ – 1}} = 6 – a\) A1
associative: \(a * (b * c) = a * (b + c – 3) = a + b + c – 6\) A1
\(\left( {a{\text{ }}*{\text{ }}b} \right){\text{ }}*{\text{ }}c{\text{ }} = \left( {a{\text{ }} + {\text{ }}b{\text{ }} – {\text{ }}3} \right)*{\text{ }}c{\text{ }} = {\text{ }}a{\text{ }} + {\text{ }}b{\text{ }} + {\text{ }}c{\text{ }} – {\text{ }}6\) A1
associative because \(a * (b * c) = (a * b) * c\) R1
\(b * a = b + a – 3 = a + b – 3 = a * b\) therefore commutative hence Abelian R1
hence \(\{ \mathbb{Z},{\text{ }} * \} \) is an Abelian group AG
[9 marks]
if \(a\) is of order 2 then \(a * a = 2a – 3 = 3\) therefore \(a = 3\) A1
which is a contradiction
since \(e = 3\) and has order 1 R1
Note: R1 for recognising that the identity has order 1.
[2 marks]
for example \(S = \{ – 6,{\text{ }} – 3,{\text{ }}0,{\text{ }}3,{\text{ }}6 \ldots \} \) or \(S = \{ \ldots ,{\text{ }} – 1,{\text{ }}1,{\text{ }}3,{\text{ }}5,{\text{ }}7 \ldots \} \) A1R1
Note: R1 for deducing, justifying or verifying that \(\left\{ {S, * } \right\}\) is indeed a proper subgroup.
[2 marks]
we need to show that \(f(a * b) = f(a) \circ f(b)\) R1
\(f(a * b) = f(a + b – 3) = a + b – 9\) A1
\(f(a) \circ f(b) = (a – 6) \circ (b – 6) = a + b – 9\) A1
hence isomorphic AG
Note: R1 for recognising that \(f\) preserves the operation; award R1A0A0 for an attempt to show that \(f(a \circ b) = f(a) * f(b)\).
[3 marks]
Question
The binary operation \( * \) is defined by
\(a * b = a + b – 3\) for \(a,{\text{ }}b \in \mathbb{Z}\).
The binary operation \( \circ \) is defined by
\(a \circ b = a + b + 3\) for \(a,{\text{ }}b \in \mathbb{Z}\).
Consider the group \(\{ \mathbb{Z},{\text{ }} \circ {\text{\} }}\) and the bijection \(f:\mathbb{Z} \to \mathbb{Z}\) given by \(f(a) = a – 6\).
a.Show that \(\{ \mathbb{Z},{\text{ }} * \} \) is an Abelian group.[9]
b.Show that there is no element of order 2.[2]
c.Find a proper subgroup of \(\{ \mathbb{Z},{\text{ }} * \} \).[2]
d.Show that the groups \(\{ \mathbb{Z},{\text{ }} * \} \) and \(\{ \mathbb{Z},{\text{ }} \circ \} \) are isomorphic.[3]
▶️Answer/Explanation
Markscheme
closure: \(\{ \mathbb{Z},{\text{ }} * \} \) is closed because \(a + b – 3 \in \mathbb{Z}\) R1
identity: \(a * e = a + e – 3 = a\) (M1)
\(e = 3\) A1
inverse: \(a * {a^{ – 1}} = a + {a^{ – 1}} – 3 = 3\) (M1)
\({a^{ – 1}} = 6 – a\) A1
associative: \(a * (b * c) = a * (b + c – 3) = a + b + c – 6\) A1
\(\left( {a{\text{ }}*{\text{ }}b} \right){\text{ }}*{\text{ }}c{\text{ }} = \left( {a{\text{ }} + {\text{ }}b{\text{ }} – {\text{ }}3} \right)*{\text{ }}c{\text{ }} = {\text{ }}a{\text{ }} + {\text{ }}b{\text{ }} + {\text{ }}c{\text{ }} – {\text{ }}6\) A1
associative because \(a * (b * c) = (a * b) * c\) R1
\(b * a = b + a – 3 = a + b – 3 = a * b\) therefore commutative hence Abelian R1
hence \(\{ \mathbb{Z},{\text{ }} * \} \) is an Abelian group AG
[9 marks]
if \(a\) is of order 2 then \(a * a = 2a – 3 = 3\) therefore \(a = 3\) A1
which is a contradiction
since \(e = 3\) and has order 1 R1
Note: R1 for recognising that the identity has order 1.
[2 marks]
for example \(S = \{ – 6,{\text{ }} – 3,{\text{ }}0,{\text{ }}3,{\text{ }}6 \ldots \} \) or \(S = \{ \ldots ,{\text{ }} – 1,{\text{ }}1,{\text{ }}3,{\text{ }}5,{\text{ }}7 \ldots \} \) A1R1
Note: R1 for deducing, justifying or verifying that \(\left\{ {S, * } \right\}\) is indeed a proper subgroup.
[2 marks]
we need to show that \(f(a * b) = f(a) \circ f(b)\) R1
\(f(a * b) = f(a + b – 3) = a + b – 9\) A1
\(f(a) \circ f(b) = (a – 6) \circ (b – 6) = a + b – 9\) A1
hence isomorphic AG
Note: R1 for recognising that \(f\) preserves the operation; award R1A0A0 for an attempt to show that \(f(a \circ b) = f(a) * f(b)\).
[3 marks]
Question
Associativity and commutativity are two of the five conditions for a set S with the binary operation \( * \) to be an Abelian group; state the other three conditions.[2]
The Cayley table for the binary operation \( \odot \) defined on the set T = {p, q, r, s, t} is given below.
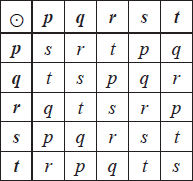
(i) Show that exactly three of the conditions for {T , \( \odot \)} to be an Abelian group are satisfied, but that neither associativity nor commutativity are satisfied.
(ii) Find the proper subsets of T that are groups of order 2, and comment on your result in the context of Lagrange’s theorem.
(iii) Find the solutions of the equation \((p \odot x) \odot x = x \odot p\) .[15]
▶️Answer/Explanation
Markscheme
closure, identity, inverse A2
Note: Award A1 for two correct properties, A0 otherwise.
[2 marks]
(i) closure: there are no extra elements in the table R1
identity: s is a (left and right) identity R1
inverses: all elements are self-inverse R1
commutative: no, because the table is not symmetrical about the leading diagonal, or by counterexample R1
associativity: for example, \((pq)t = rt = p\) M1A1
not associative because \(p(qt) = pr = t \ne p\) R1
Note: Award M1A1 for 1 complete example whether or not it shows non-associativity.
(ii) \(\{ s,\,p\} ,{\text{ }}\{ s,\,q\} ,{\text{ }}\{ s,\,r\} ,{\text{ }}\{ s,\,t\} \) A2
Note: Award A1 for 2 or 3 correct sets.
as 2 does not divide 5, Lagrange’s theorem would have been contradicted if T had been a group R1
(iii) any attempt at trying values (M1)
the solutions are q, r, s and t A1A1A1A1
Note: Deduct A1 if p is included.
[15 marks]
Question
(a) Write down why the table below is a Latin square.
\[\begin{gathered}
\begin{array}{*{20}{c}}
{}&d&e&b&a&c
\end{array} \\
\begin{array}{*{20}{c}}
d \\
e \\
b \\
a \\
c
\end{array}\left[ {\begin{array}{*{20}{c}}
c&d&e&b&a \\
d&e&b&a&c \\
a&b&d&c&e \\
b&a&c&e&d \\
e&c&a&d&b
\end{array}} \right] \\
\end{gathered} \]
(b) Use Lagrange’s theorem to show that the table is not a group table.
▶️Answer/Explanation
Markscheme
(a) Each row and column contains all the elements of the set. A1A1
[2 marks]
(b) There are 5 elements therefore any subgroup must be of an order that is a factor of 5 R2
But there is a subgroup \(\begin{gathered}
\begin{array}{*{20}{c}}
{}&e&a
\end{array} \\
\begin{array}{*{20}{c}}
e \\
a
\end{array}\left( {\begin{array}{*{20}{c}}
e&a \\
a&e
\end{array}} \right) \\
\end{gathered} \) of order 2 so the table is not a group table R2
Note: Award R0R2 for “a is an element of order 2 which does not divide the order of the group”.
[4 marks]
Total [6 marks]
Examiners report
Part (a) presented no problem but finding the order two subgroups (Lagrange’s theorem was often quoted correctly) was beyond some candidates. Possibly presenting the set in non-alphabetical order was the problem.
