Question
(a) Find the six roots of the equation \({z^6} – 1 = 0\) , giving your answers in the form \(r\,{\text{cis}}\,\theta {\text{, }}r \in {\mathbb{R}^ + }{\text{, }}0 \leqslant \theta < 2\pi \) .
(b) (i) Show that these six roots form a group G under multiplication of complex numbers.
(ii) Show that G is cyclic and find all the generators.
(iii) Give an example of another group that is isomorphic to G, stating clearly the corresponding elements in the two groups.
▶️Answer/Explanation
Markscheme
(a) \({z^6} = 1 = {\text{cis}}\,2n\pi \) (M1)
The six roots are
\({\text{cis}}\,0(1),{\text{ cis}}\frac{\pi }{3},{\text{ cis}}\frac{{2\pi }}{3},{\text{ cis}}\,\pi ( – 1),{\text{ cis}}\frac{{4\pi }}{3},{\text{ cis}}\frac{{5\pi }}{3}\) A3
Note: Award A2 for 4 or 5 correct roots, A1 for 2 or 3 correct roots.
[4 marks]
(b) (i) Closure: Consider any two roots \({\text{cis}}\frac{{m\pi }}{3},{\text{ cis}}\frac{{n\pi }}{3}\). M1
\({\text{cis}}\frac{{m\pi }}{3} \times {\text{cis}}\frac{{n\pi }}{3} = {\text{cis}}\,(m + n){\text{(mod6)}}\frac{\pi }{3} \in G\) A1
Note: Award M1A1 for a correct Cayley table showing closure.
Identity: The identity is 1. A1
Inverse: The inverse of \({\text{cis}}\frac{{m\pi }}{3}{\text{ is cis}}\frac{{(6 – m)\pi }}{3} \in G\) . A2
Associative: This follows from the associativity of multiplication. R1
The 4 group axioms are satisfied. R1
(ii) Successive powers of \({\text{cis}}\frac{\pi }{3}\left( {{\text{or cis}}\frac{{5\pi }}{3}} \right)\)
generate the group which is therefore cyclic. R2
The (only) other generator is \({\text{cis}}\frac{{5\pi }}{3}\left( {{\text{or cis}}\frac{\pi }{3}} \right)\) . A1
Note: Award A0 for any additional answers.
(iii) The group of the integers 0, 1, 2, 3, 4, 5 under addition modulo 6. R2
The correspondence is
\(m \to {\text{cis}}\frac{{m\pi }}{3}\) R1
Note: Accept any other cyclic group of order 6.
[13 marks]
Total [17 marks]
Examiners report
This question was reasonably well answered by many candidates, although in (b)(iii), some candidates were unable to give another group isomorphic to G.
Question
(a) Draw the Cayley table for the set of integers G = {0, 1, 2, 3, 4, 5} under addition modulo 6, \({ + _6}\).
(b) Show that \(\{ G,{\text{ }}{ + _6}\} \) is a group.
(c) Find the order of each element.
(d) Show that \(\{ G,{\text{ }}{ + _6}\} \) is cyclic and state its generators.
(e) Find a subgroup with three elements.
(f) Find the other proper subgroups of \(\{ G,{\text{ }}{ + _6}\} \).
▶️Answer/Explanation
Markscheme
(a) 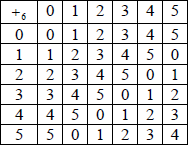 A3
A3
Note: Award A2 for 1 error, A1 for 2 errors and A0 for more than 2 errors.
[3 marks]
(b) The table is closed A1
Identity element is 0 A1
Each element has a unique inverse (0 appears exactly once in each row and column) A1
Addition mod 6 is associative A1
Hence \(\{ G,{\text{ }}{ + _6}\} \) forms a group AG
[4 marks]
(c) 0 has order 1 (0 = 0),
1 has order 6 (1 + 1 + 1 + 1 + 1 + 1 = 0),
2 has order 3 (2 + 2 + 2 = 0),
3 has order 2 (3 + 3 = 0),
4 has order 3 (4 + 4 + 4 = 0),
5 has order 6 (5 + 5 + 5 + 5 + 5 + 5 = 0). A3
Note: Award A2 for 1 error, A1 for 2 errors and A0 for more than 2 errors.
[3 marks]
(d) Since 1 and 5 are of order 6 (the same as the order of the group) every element can be written as sums of either 1 or 5. Hence the group is cyclic. R1
The generators are 1 and 5. A1
[2 marks]
(e) A subgroup of order 3 is \(\left( {\{ 0,{\text{ }}2,{\text{ }}4\} ,{\text{ }}{ + _6}} \right)\) A2
Note: Award A1 if only {0, 2, 4} is seen.
[2 marks]
(f) Other proper subgroups are \(\left( {\{ 0\} { + _6}} \right),{\text{ }}\left( {\{ 0,{\text{ }}3\} { + _6}} \right)\) A1A1
Note: Award A1 if only {0}, {0, 3} is seen.
[2 marks]
Total [16 marks]
Examiners report
The table was well done as was showing its group properties. The order of the elements in (b) was done well except for the order of 0 which was often not given. Finding the generators did not seem difficult but correctly stating the subgroups was not often done. The notion of a ‘proper’ subgroup is not well known.
Question
(a) Show that {1, −1, i, −i} forms a group of complex numbers G under multiplication.
(b) Consider \(S = \{ e,{\text{ }}a,{\text{ }}b,{\text{ }}a * b\} \) under an associative operation \( * \) where e is the identity element. If \(a * a = b * b = e\) and \(a * b = b * a\) , show that
(i) \(a * b * a = b\) ,
(ii) \(a * b * a * b = e\) .
(c) (i) Write down the Cayley table for \(H = \{ S{\text{ , }} * \} \).
(ii) Show that H is a group.
(iii) Show that H is an Abelian group.
(d) For the above groups, G and H , show that one is cyclic and write down why the other is not. Write down all the generators of the cyclic group.
(e) Give a reason why G and H are not isomorphic.
▶️Answer/Explanation
Markscheme
(a)
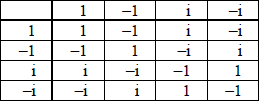
see the Cayley table, (since there are no new elements) the set is closed A1
1 is the identity element A1
1 and –1 are self inverses and i and -i form an inverse pair, hence every element has an inverse A1
multiplication is associative A1
hence {1, –1, i, –i} form a group G under the operation of multiplication AG
[4 marks]
(b) (i) aba = aab
= eb A1
= b AG
(ii) abab = aabb
= ee A1
= e AG
[2 marks]
(c) (i)
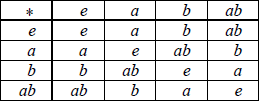 A2
A2
Note: Award A1 for 1 or 2 errors, A0 for more than 2.
(ii) see the Cayley table, (since there are no new elements) the set is closed A1
H has an identity element e A1
all elements are self inverses, hence every element has an inverse A1
the operation is associative as stated in the question
hence {e , a , b , ab} forms a group G under the operation \( * \) AG
(iii) since there is symmetry across the leading diagonal of the group table, the group is Abelian A1
[6 marks]
(d) consider the element i from the group G (M1)
\({{\text{i}}^2} = – 1\)
\({{\text{i}}^3} = – {\text{i}}\)
\({{\text{i}}^4} = 1\)
thus i is a generator for G and hence G is a cyclic group A1
–i is the other generator for G A1
for the group H there is no generator as all the elements are self inverses R1
[4 marks]
(e) since one group is cyclic and the other group is not, they are not isomorphic R1
[1 mark]
Total [17 marks]
Examiners report
Most candidates were aware of the group axioms and the properties of a group, but they were not always explained clearly. A number of candidates did not understand the term “Abelian”. Many candidates understood the conditions for a group to be cyclic. Many candidates did not realise that the answer to part (e) was actually found in part (d), hence the reason for this part only being worth 1 mark. Overall, a number of fully correct solutions to this question were seen.
Question
Let G be a finite cyclic group.
(a) Prove that G is Abelian.
(b) Given that a is a generator of G, show that \({a^{ – 1}}\) is also a generator.
(c) Show that if the order of G is five, then all elements of G, apart from the identity, are generators of G.
▶️Answer/Explanation
Markscheme
(a) let a be a generator and consider the (general) elements \(b = {a^m},{\text{ }}c = {a^n}\) M1
then
\(bc = {a^m}{a^n}\) A1
\( = {a^n}{a^m}\) (using associativity) R1
\( = cb\) A1
therefore G is Abelian AG
[4 marks]
(b) let G be of order p and let \(m \in \{ 1,…….,{\text{ }}p\} \), let a be a generator
consider \(a{a^{ – 1}} = e \Rightarrow {a^m}{({a^{ – 1}})^m} = e\) M1R1
this shows that \({({a^{ – 1}})^m}\) is the inverse of \({a^m}\) R1
as m increases from 1 to p, \({a^m}\) takes p different values and it generates G R1
it follows from the uniqueness of the inverse that \({({a^{ – 1}})^m}\) takes p different values and is a generator R1
[5 marks]
(c) EITHER
by Lagrange, the order of any element divides the order of the group, i.e. 5 R1
the only numbers dividing 5 are 1 and 5 R1
the identity element is the only element of order 1 R1
all the other elements must be of order 5 R1
so they all generate G AG
OR
let a be a generator.
successive powers of a and therefore the elements of G are
\(a,{\text{ }}{a^2},{\text{ }}{a^3},{\text{ }}{a^4}{\text{ and }}{a^5} = e\) A1
successive powers of \({a^2}\) are \({a^2},{\text{ }}{a^4},{\text{ }}a,{\text{ }}{a^3},{\text{ }}{a^5} = e\) A1
successive powers of \({a^3}\) are \({a^3},{\text{ }}a,{\text{ }}{a^4},{\text{ }}{a^2},{\text{ }}{a^5} = e\) A1
successive powers of \({a^4}\) are \({a^4},{\text{ }}{a^3},{\text{ }}{a^2},{\text{ }}a,{\text{ }}{a^5} = e\) A1
this shows that \({a^2},{\text{ }}{a^3},{\text{ }}{a^4}\) are also generators in addition to a AG
[4 marks]
Total [13 marks]
Examiners report
Solutions to (a) were often disappointing with some solutions even stating that a cyclic group is, by definition, commutative and therefore Abelian. Explanations in (b) were often poor and it was difficult in some cases to distinguish between correct and incorrect solutions. In (c), candidates who realised that Lagrange’s Theorem could be used were generally the most successful. Solutions again confirmed that, in general, candidates find theoretical questions on this topic difficult.
Question
Set \(S = \{ {x_0},{\text{ }}{x_1},{\text{ }}{x_2},{\text{ }}{x_3},{\text{ }}{x_4},{\text{ }}{x_5}\} \) and a binary operation \( \circ \) on S is defined as \({x_i} \circ {x_j} = {x_k}\), where \(i + j \equiv k(\bmod 6)\).
(a) (i) Construct the Cayley table for \(\{ S,{\text{ }} \circ \} \) and hence show that it is a group.
(ii) Show that \(\{ S,{\text{ }} \circ \} \) is cyclic.
(b) Let \(\{ G,{\text{ }} * \} \) be an Abelian group of order 6. The element \(a \in {\text{G}}\) has order 2 and the element \(b \in {\text{G}}\) has order 3.
(i) Write down the six elements of \(\{ G,{\text{ }} * \} \).
(ii) Find the order of \({\text{a}} * b\) and hence show that \(\{ G,{\text{ }} * \} \) is isomorphic to \(\{ S,{\text{ }} \circ \} \).
▶️Answer/Explanation
Markscheme
(a) (i) Cayley table for \(\{ S,{\text{ }} \circ \} \)
\(\begin{array}{*{20}{c|cccccc}}
\circ &{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}} \\
\hline
{{x_0}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}} \\
{{x_1}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}} \\
{{x_2}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}} \\
{{x_3}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}} \\
{{x_4}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}} \\
{{x_5}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}
\end{array}\) A4
Note: Award A4 for no errors, A3 for one error, A2 for two errors, A1 for three errors and A0 for four or more errors.
S is closed under \( \circ \) A1
\({x_0}\) is the identity A1
\({x_0}\) and \({x_3}\) are self-inverses, A1
\({x_2}\) and \({x_4}\) are mutual inverses and so are \({x_1}\) and \({x_5}\) A1
modular addition is associative A1
hence, \(\{ S,{\text{ }} \circ \} \) is a group AG
(ii) the order of \({x_1}\) (or \({x_5}\)) is 6, hence there exists a generator, and \(\{ S,{\text{ }} \circ \} \) is a cyclic group A1R1
[11 marks]
(b) (i) e, a, b, ab A1
and \({b^2},{\text{ }}a{b^2}\) A1A1
Note: Accept \(ba\) and \({b^2}a\).
(ii) \({(ab)^2} = {b^2}\) M1A1
\({(ab)^3} = a\) A1
\({(ab)^4} = b\) A1
hence order is 6 A1
groups G and S have the same orders and both are cyclic R1
hence isomorphic AG
[9 marks]
Total [20 marks]
Examiners report
a) Most candidates had the correct Cayley table and were able to show successfully that the group axioms were satisfied. Some candidates, however, simply stated that an inverse exists for each element without stating the elements and their inverses. Most candidates were able to find a generator and hence show that the group is cyclic.
b) This part was answered less successfully by many candidates. Some failed to find all the elements. Some stated that the order of ab is 6 without showing any working.
