IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 2.1 – Motion
Topic 2 Weightage : 9 %
All Questions for Topic 2.1 – Distance and displacement , Speed and velocity , Acceleration , Graphs describing motion , Equations of motion for uniform acceleration , Projectile motion , Fluid resistance and terminal speed
Question
A boy throws a ball horizontally at a speed of 15 m s–1 from the top of a cliff that is 80 m above the surface of the sea. Air resistance is negligible.
What is the distance from the bottom of the cliff to the point where the ball lands in the sea?
45 m
60 m
80 m
240 m
▶️Answer/Explanation
Ans: B
Assuming constant vertical acceleration, no horizontal acceleration, and no air resistance:
\(y(t) =y_0+\dot{y_0}t+\frac{1}{2}\ddot{y}t^2\)
Then when \(y(t_1)=y_1\)
\(\frac{\ddot{y}}{2}t_1^2+\dot{y_0t_1}+(y_0-y_1)=0)\)
so by quadratic formula
\(t_1=\frac{-\dot{y_0}\pm \sqrt{\dot{y}_0^2-4 \times \frac{\ddot{y}}{2}\times(y_0-y_1)}}{2 \times \frac{\ddot{y}}{2}}\)
Given
\(\dot{y_0}=0\;m/s\)
\(\ddot{y}=g< 0\)
\(t_1\geq 0\)
we can reduce that to
\(t_1=\frac{\sqrt{-2g(y_0-y_1)}}{-g}=\sqrt{\frac{2(y_1-y_0)}{g}}\)
In that same time the stone has moved \(\dot{x_0}t_1 \;m\) horizontally.
Given
\(\dot{x_0}=15 ms^{-1}\)
\(y_0=80m \)
\(y_1=0 m\)
\(g=-9.81 ms^{-2}\)
we get
\(x_1\) = 60 m
Question
Two isolated spherical planets have the same gravitational potential at their surfaces. Which ratio must also be the same for the two planets?
A. \(\frac{{{\rm{radiu}}{{\rm{s}}^{\rm{3}}}}}{{{\rm{mass}}}}\)
B. \(\frac{{{\rm{radiu}}{{\rm{s}}^{\rm{2}}}}}{{{\rm{mass}}}}\)
C. \(\frac{{{\rm{radius}}}}{{{\rm{mass}}}}\)
D. radius
▶️Answer/Explanation
Markscheme
C
The amount of work done in moving a unit test mass from infinity into the gravitational influence of source mass is known as gravitational potential.
Simply, it is the gravitational potential energy possessed by a unit test mass
⇒ V = U/m
⇒ V = -GM/R
Now two planet has same potential on surface means Vp1=Vp2
or
\(\frac{-GM_1}{R_1}=\frac{-GM_2}{R_2}\)
or
\(\frac{M}{R}=constant\)
or
\(\frac{R}{M}=constant\)
Question
A ball of mass m is projected horizontally with speed v from a height h above the floor. Air resistance is negligible.
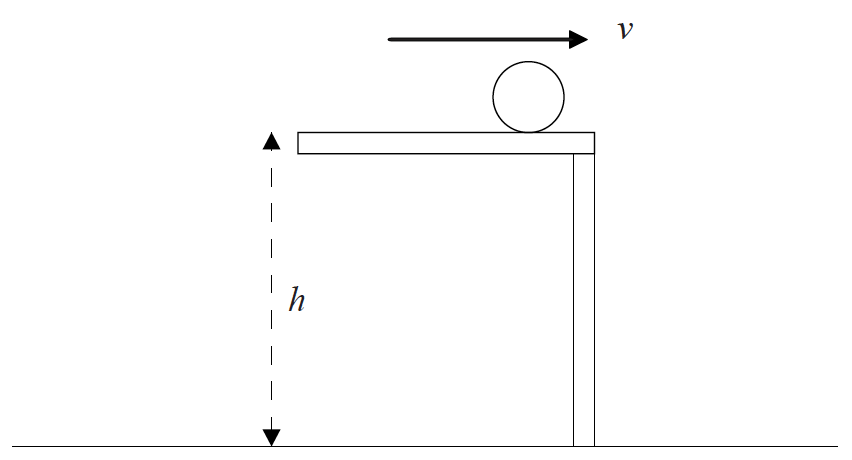
The horizontal distance travelled by the ball to the point where it lands on the floor depends on
A. m and h only.
B. m and v only.
C. h and v only.
D. m, h and v.
▶️Answer/Explanation
Markscheme
C
Refer : https://www.iitianacademy.com/ib-physics-unit-2-mechanics-motion-notes/
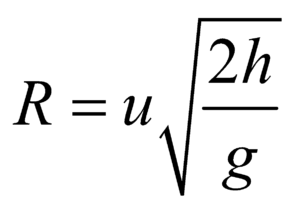

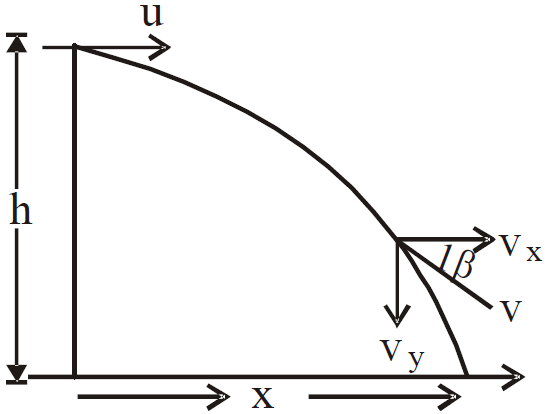
Question
A student throws a stone with velocity \(v\) at an angle \(\theta \) to the vertical from the surface of a lake. Air resistance can be ignored. The acceleration due to gravity is \(g\).

What is the time taken for the stone to hit the surface of the lake?
A. \(\frac{{v\sin \theta }}{g}\)
B. \(\frac{{v\cos \theta }}{g}\)
C. \(\frac{{2v\sin \theta }}{g}\)
D. \(\frac{{2v\cos \theta }}{g}\)
▶️Answer/Explanation
Markscheme
D
